In this GitHub repository the user can here find the code used to reproduce the plots and the results in our paper[1]. We propose the novel application of deep unfolding to the weighted minimum mean square error (WMMSE) algorithm in [2]. The WMMSE is an iterative algorithm that converges to a local solution of the weigthed sum rate maximization problem subject to a power constraint, which is known to be NP-hard. As noted in [3], the formulation of the WMMSE algorithm, as described in [2], is not suitable to be unfolded due to a matrix inversion, an eigendecomposition, and a bisection search performed at each itearation. Therefore, in our paper [1], we propose an alternative formulation that avoids these operations. Specifically, we replace the method of Lagrange multipliers with the projected gradient descent (PGD) approach. In this way the matrix inversion, the eigendecomposition, and the bisection search are replaced by simple vector operations.
In the jupyter notebook "Unfolded_WMMSE_versus_WMMSE.ipynb" the user can find the implementation in Python 3.6.8 of the WMMSE algorithm in [2] and the implementation in Python 3.6.8 and Tensorflow 1.13.1 of our proposed unfolded WMMSE algorithm [1]. The notebook cells should be run in sequential order. Note that the training time can vary from an hour to many hours, depending on the parameter settings, e.g., the number of iterations and the number of PGS steps, and on the user hardware.
Let be the transmitted data symbol to user
and let
be the channel between the base station and user
.
With linear beamforming, the signal at the receiver of user is
where is the transmit beamformer for user
and where
is independent additive white Gaussian noise with power
. The signal-to-interference-plus-noise-ratio (SINR) of user
is
The estimated data symbol at the receiver of user is
, where
is the receiver gain.
We seek to maximize the weighted sum rate (WSR) subject to a total transmit power constraint, i.e.,
where indicates the user priority (assumed to be known) and where
is the maximum transmit power at the base station. We assume to have perfect channel knowledge. This problem is known to be NP-hard.
We define
,
,
, and
.
Algorithm 1 reports the pseudocode of the unfoldable WMMSE and Fig 1 depicts the overall neural network architecture.
indexes the users,
indexes the layers/iterations, and
indexes the PGD steps.
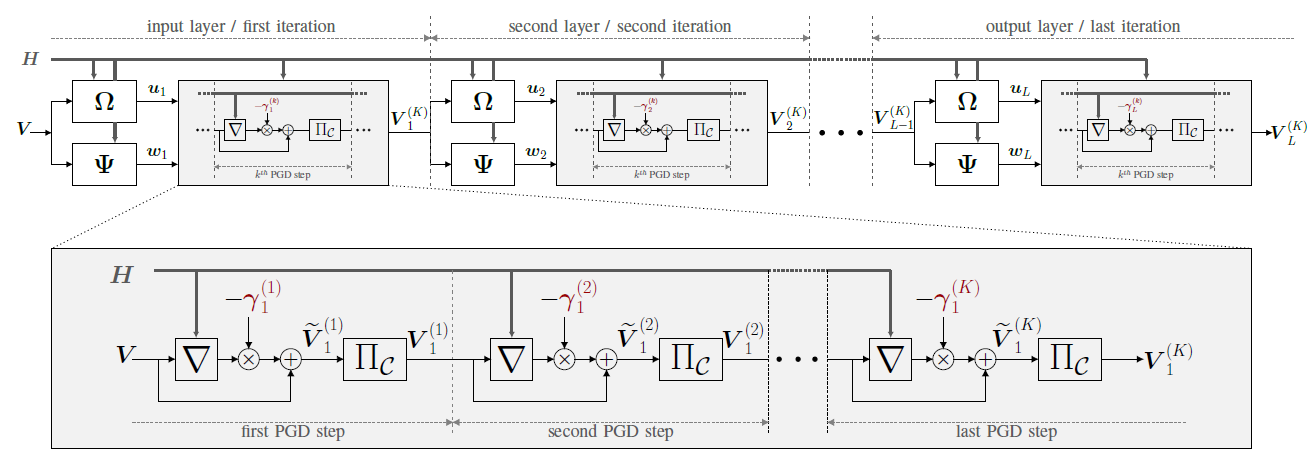Fig. 1. The neural network architecture obtained by unfolding iterations of the WMMSE and
projected gradient descent (PGD) steps per iteration. The subscript
corresponds to the
layer/iteration and the superscript
corresponds to the
PGD step. The trainable parameters, highlighted in red, are the step sizes of the PGD approach. Each layer of the neural network is given by the update equation of
, indicated by
, by the update equation of
, indicated by
, and by unfolding
PGD steps, as depicted in the gray box. In particular,
and
indicate the gradient and the projection operations, respectively.
In order to run the code in this repository the following software packages are needed:
Python 3(for reference we use Python 3.6.8), with the following packages:numpy,tensorflow(version 1.x - for reference we use version 1.13.1),matplotlib,copy,time.Jupyter(for reference we use version 6.0.3).
[1] L. Pellaco, M. Bengtsson, J. Jaldén, "Deep unfolding of the weighted MMSE algorithm," submitted to IEEE Transactions on Signal Processing, 2020.
[2] Q. Shi, M. Razaviyayn, Z. Luo and C. He, "An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel," in IEEE Transactions on Signal Processing, vol. 59, no. 9, pp. 4331-4340, Sept. 2011, doi: 10.1109/TSP.2011.2147784.
[3] H. Sun, X. Chen, Q. Shi, M. Hong, X. Fu and N. D. Sidiropoulos, "Learning to Optimize: Training Deep Neural Networks for Interference Management," in IEEE Transactions on Signal Processing, vol. 66, no. 20, pp. 5438-5453, 15 Oct.15, 2018, doi: 10.1109/TSP.2018.2866382.