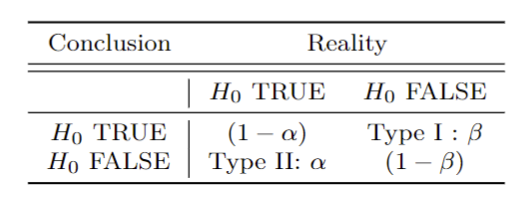
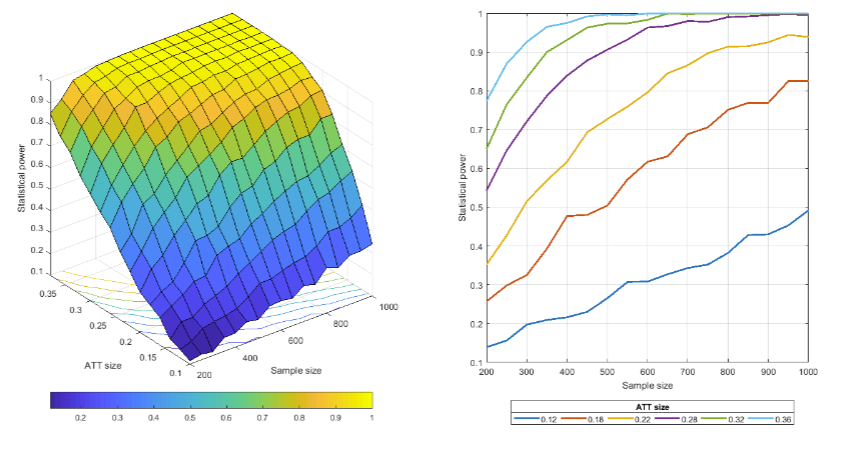
Statistical power
To estimate the power of our main specification, we use Monte Carlo simulation by replicating the data generating process of our experiment:
where F is a very general distribution and can be as complex as desired.
Given this synthetic data, together with an identification method we will estimate the parameters of interest of the model and compute its power. For instance, we might use a linear conditional mean model:
In general, we will describe (approximate) power as a function of sample size and effect size, and it will be a non-decreasing function in this two arguments.
In this repository you can find several examples of power simulations of varying complexity.