This repo is the official source code of NeurIPS-2024 paper:
Where Do Large Learning Rates Lead Us?
By Ildus Sadrtdinov*,
Maxim Kodryan*,
Eduard Pokonechny*,
Ekaterina Lobacheva†,
Dmitry Vetrov†
* — equal contribution; † — shared senior authorship
arXiv / OpenReview / Poster & video / X thread
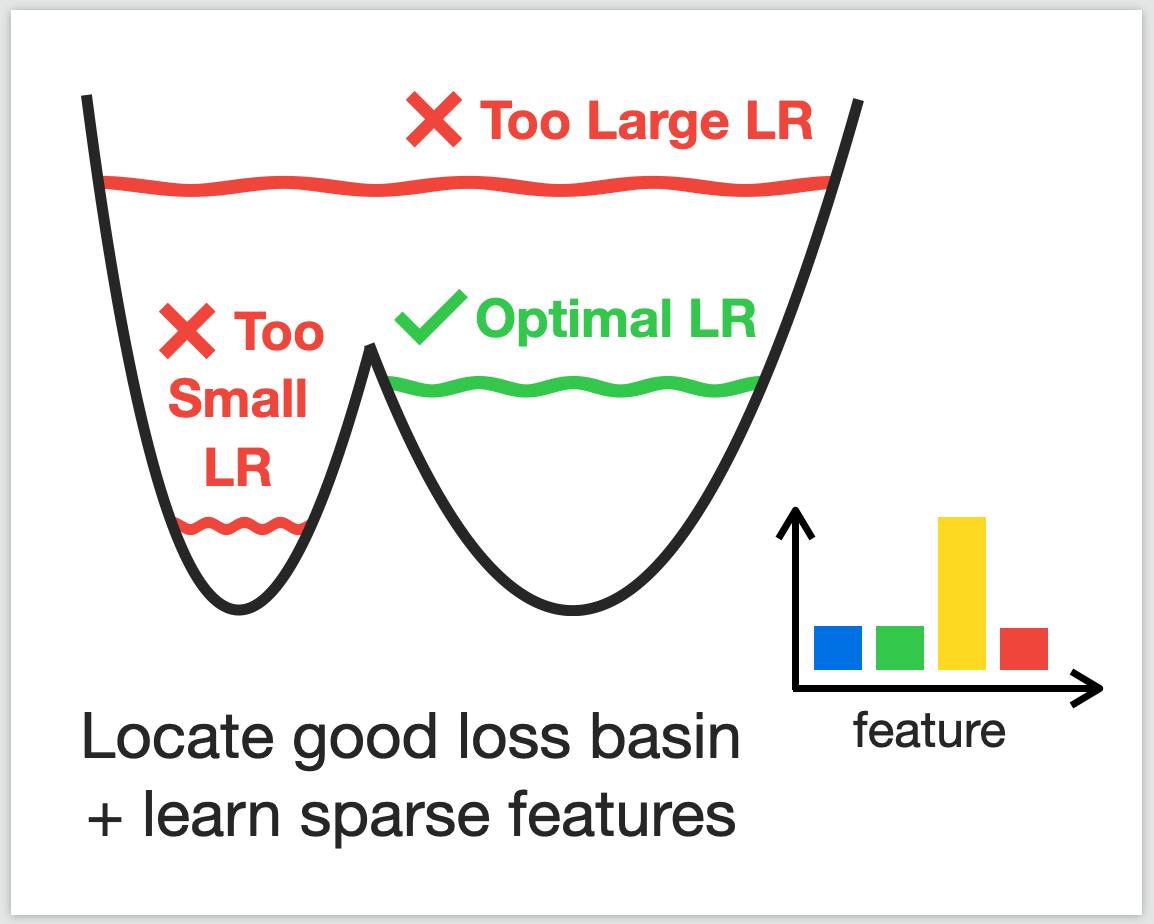 It is generally accepted that starting neural networks training with large learning rates (LRs) improves generalization.
Following a line of research devoted to understanding this effect, we conduct an empirical study in a controlled setting
focusing on two questions: 1) how large an initial LR is required for obtaining optimal quality, and
2) what are the key differences between models trained with different LRs?
We discover that only a narrow range of initial LRs slightly above the convergence threshold
lead to optimal results after fine-tuning with a small LR or weight averaging.
By studying the local geometry of reached minima, we observe that using LRs from this optimal range
allows for the optimization to locate a basin that only contains high-quality minima.
Additionally, we show that these initial LRs result in a sparse set of learned features,
with a clear focus on those most relevant for the task. In contrast, starting training with too small LRs
leads to unstable minima and attempts to learn all features simultaneously, resulting in poor generalization.
Conversely, using initial LRs that are too large fails to detect a basin with good solutions and extract meaningful patterns from the data.
It is generally accepted that starting neural networks training with large learning rates (LRs) improves generalization.
Following a line of research devoted to understanding this effect, we conduct an empirical study in a controlled setting
focusing on two questions: 1) how large an initial LR is required for obtaining optimal quality, and
2) what are the key differences between models trained with different LRs?
We discover that only a narrow range of initial LRs slightly above the convergence threshold
lead to optimal results after fine-tuning with a small LR or weight averaging.
By studying the local geometry of reached minima, we observe that using LRs from this optimal range
allows for the optimization to locate a basin that only contains high-quality minima.
Additionally, we show that these initial LRs result in a sparse set of learned features,
with a clear focus on those most relevant for the task. In contrast, starting training with too small LRs
leads to unstable minima and attempts to learn all features simultaneously, resulting in poor generalization.
Conversely, using initial LRs that are too large fails to detect a basin with good solutions and extract meaningful patterns from the data.
If you found this code useful, please cite our paper:
@inproceedings{sadrtdinov2024where,
title={Where Do Large Learning Rates Lead Us?},
author={Ildus Sadrtdinov and Maxim Kodryan and Eduard Pokonechny and Ekaterina Lobacheva and Dmitry Vetrov},
booktitle={The Thirty-eighth Annual Conference on Neural Information Processing Systems (NeurIPS)},
year={2024},
}