This system is designed for bodies of water ranging from a small pond to the ocean as viewed from a island. Although not a rigorous physical simulation, it does deliver convincing, flexible, and dynamic renderings of water. Because the simulation runs entirely on the GPU, it entails no struggle over CPU usage with either artificial intelligence (AI) or physics processes. Because the system parameters do have a physical basis, they are easier to script than if they were found by trial and error. Making the system as a whole dynamic—in addition to its component waves—adds an extra level of life.
We start by a creating 64 X 64 mesh of nodes holding the information of position and normals placing them equidistant from each other in a homogenous fashion. Then we translate the xyz components of the nodes based on the equations mentioned in the following sections.
To provide variation in the dynamics of the scene, we will randomly generate these wave parameters within constraints. Over time, we will continuously fade one wave out and then fade it back in with a different set of parameters. As it turns out, these parameters are interdependent. Care must be taken to generate an entire set of parameters for each wave that combine in a convincing manner.
##Basic Mathematics Involved :- We use Gerstner Waves to model our waves whose equations are given by :-
where,
Q - A parameter that controls the steepness of the waves
A - Amplitude
D - Direction vector of the wave
w - frequency (relates to wavelength(L) as square root of gravity x 2p/L)
(x,y) - Initial position of the node on x,y plane

t - time
##Wave Trains We generate multiple wave trains (10 in our case) at initialization all with different parameters and slowly fade in all the trains. The final position of each node is calculated by adding all the wave trains and reaching a final result. We set a life for each of the wave train and fade out the wave train when its life ends. Following this approach, old wave trains keep on dying away and new wave trains keep on generating giving a random look to the ocean surface.
##Choosing the parameters
We select a median wavelength and generate random wavelengths between half and double that length.
Given frequency we can calculate the frequency as :-
we set a ratio of amplitude to wavelength in accordance with the formula w * A < 1, and use that ratio throughout to calculate the Amplitude.
We set a wind vector at the initialization, and calcuate the the direction randomly within a constant angle of the wind direction.
Speed is independent of all other variables, we can choose any random value for that, although here, I have taken the speed to be predefined constant thorughout the simulation
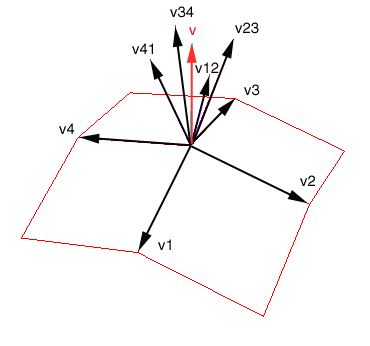
We can calculate the normal for each vertex using the three vertices(v1,v2,v3) of the triangle by using this method :-
u = v1-v3
v = v1-v2
normal = u X v
v1.normal = v2.normal = v3.normal = normal Since each vertex is shared among around 8 triangles, we average out the normals and then normalize them as shown in the figure.
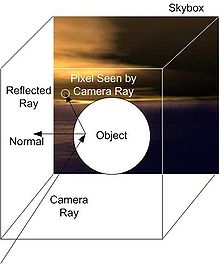
For the shading the mesh I have used a reflection model in which the mesh reflects the environment as per the normal of each vertex. In my shader, I cast a ray from the position of the camera towards the node position which bounces of the surface making an equal angle of reflection as incidence angle with respect to the normal (as shown in the image) of the node to get the pixel value of the texture around our wave (Here I have used a skybox to bound the environment).