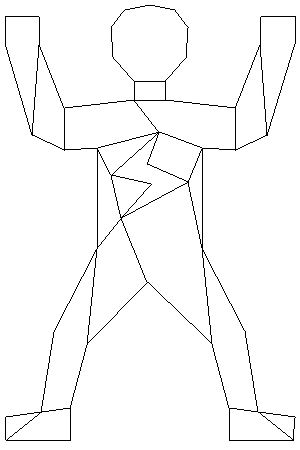
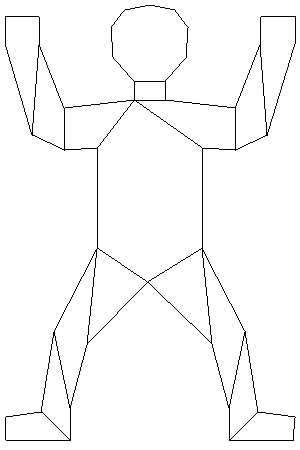
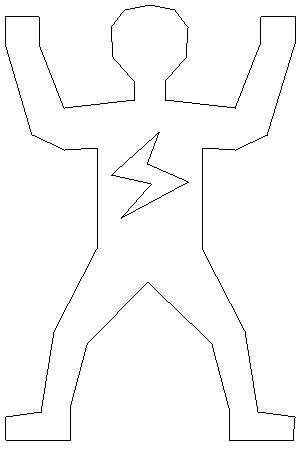PolyPartition is a lightweight C++ library for polygon partition and triangulation. PolyPartition implements multiple algorithms for both convex partitioning and triangulation. Different algorithms produce different quality of results (and their complexity varies accordingly). The implemented methods/algorithms with their advantages and disadvantages are outlined below.
For input parameters and return values see method declarations
in polypartition.h. All methods require that the input polygons
are not self-intersecting, are defined in the correct vertex order
(counter-clockwise for non-holes, clockwise for holes), and any holes
must be explicitly marked as holes (you can use SetHole(true)).
Polygon vertices can easily be ordered correctly by
calling TPPLPoly::SetOrientation method.
Input polygon:
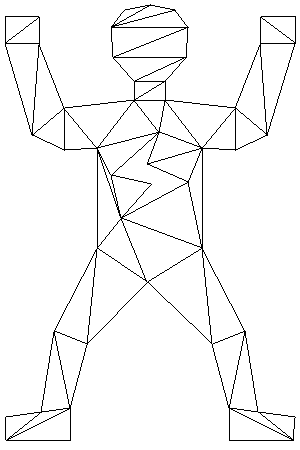
Method: TPPLPartition::Triangulate_EC
Time/Space complexity: O(n^2)/O(n)
Supports holes: Yes, by calling TPPLPartition::RemoveHoles.
Quality of solution: Satisfactory in most cases.
Example:
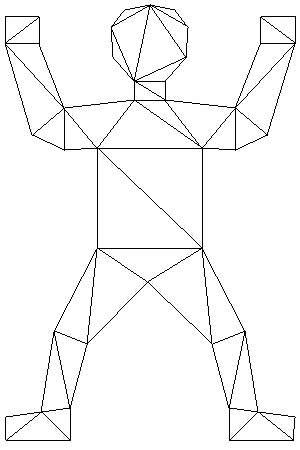
Method: TPPLPartition::Triangulate_OPT
Time/Space complexity: O(n^3)/O(n^2)
Supports holes: No. You could call TPPLPartition::RemoveHoles prior
to calling TPPLPartition::Triangulate_OPT, but the solution would no
longer be optimal, thus defeating the purpose.
Quality of solution: Optimal in terms of minimal edge length.
Example:
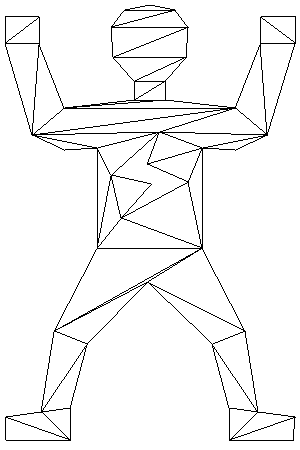
Method: TPPLPartition::Triangulate_MONO
Time/Space complexity: O(n*log(n))/O(n)
Supports holes: Yes, by design
Quality of solution: Poor. Many thin triangles are created in most cases.
Example:
Method: TPPLPartition::ConvexPartition_HM
Time/Space complexity: O(n^2)/O(n)
Supports holes: Yes, by calling TPPLPartition::RemoveHoles.
Quality of solution: At most four times the minimum number of convex polygons is created. However, in practice it works much better than that and often gives optimal partition.
Example:
Method: TPPLPartition::ConvexPartition_OPT
Time/Space complexity: O(n^3)/O(n^3)
Supports holes: No. You could call TPPLPartition::RemoveHoles
prior to calling TPPLPartition::Triangulate_OPT, but the solution
would no longer be optimal, thus defeating the purpose.
Quality of solution: Optimal. A minimum number of convex polygons is produced.
Example: