Este repositório apresenta a solução implementada para um desafio da disciplina de Algoritmos e Estruturas de Dados. Há com isso o propósito de testar a implementação de um algoritmo guloso que faça pesquisa em uma matriz. Para melhor entendimento deste trabalho, considere as sentenças à seguir:
-
$K$ - Número de matrizes de entrada. -
$N$ - Ordem de uma matriz tal que$N \in \mathbb{Z}$ e$N\geq 0$ . -
$i$ - Índice de uma linha que pertence à uma matriz específica, também pode ser abstraído como deslocamento na vertical, tal que$i \geq 0$ e$i \in \mathbb{Z}$ . -
$j$ - Índice de uma coluna que pertence à uma matriz específica, também pode ser abstraído como deslocamento na horizontal, tal que$j \geq 0$ e$j \in \mathbb{Z}$ . -
$a_{ij}$ - Elemento encontrado quando há deslocamento até a linha de índice$i$ e coluna de índice$j$ . -
Nomes de diretórios, ou arquivos serão referênciados da seguinte forma:
Nome.txtouDiretório_2. -
Nomes de comandos digitados no terminal,funções ou variáveis serão referênciados da seguinte forma: touch main.cpp, make run, ShowResults(), variableA.
-
Para as Figuras de 1 à 10, considere a legenda de cores:
- Azul:Uma posição futura possível.
- Cinza: Uma posição futura impossível.
- Laranja: Posição atual ou inicial.
- Rosa: Posição futura escolhida.
A problemática proposta incita os alunos da disciplina a desenvolverem um programa que leia
-
As matrizes deverão estar préviamente organizadas para processamento.
-
A pesquisa ou percorrimento na matriz iniciará à partir da entrada de dados do usuário ou de um arquivo. Esta entrada é o ponto de onde caminhada ou pesquisa pela matriz se inicia.
-
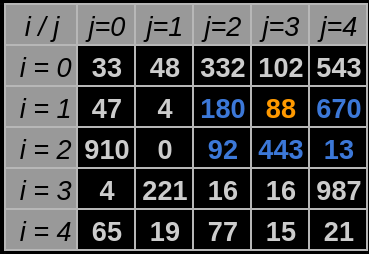
Os movimentos válidos para deslocamento pela matriz são listados à seguir e visualizados de azul na Figura 1, considerando o ponto de partida atual sendo o elemento colorido de laranja:
-
Avançar para a próxima coluna.
-
Retroceder a coluna anterior.
-
Avançar para a linha de baixo.
-
Avançar em diagonal esquerda, ou direita para baixo.
-
Fonte: Construção pelo autor¹.
____________________________________________
¹Criada usando o Google Sheets, Disponível em Planilha.
- Os movimentos devem ser realizados em direção às casas adjascentes de maior valor possível. No caso da Figura 1 essa opção representa o elemento em
$i=1$ e$j=4$ , portanto o próximo movimento se desloca até$a_{14}$ . - Caso haja um valor em comum entre as direções de maior valor, é necessário que uma regra de caminhamento seja estabelecida. E que esta enquanto padrão seja a melhor decisão de caminhamento.
- Ao ter como posição atual o elemento de uma matriz posicionado na última linha e coluna simultâneamente, ou seja o elemento na coordenada de maior valor referente a
$i$ e$j$ , tais que,$i,j \in \mathbb{Z}$ onde $ 0 \leq i\leq N$ e$0 \leq j \leq N$ , considera-se que a matriz foi percorrida até o final com isso o programa recebe uma nova entrada referênte ao ponto inicial de caminhada para a próxima matriz. Caso o programa tenha lido a última matriz, isso não acontece.
Os arquivos para funcionamento do projeto são:
input.data: Um arquivo que armazena na sua primeira linha a ordem das matrizes que estão dispostas nas linhas subsequentes.
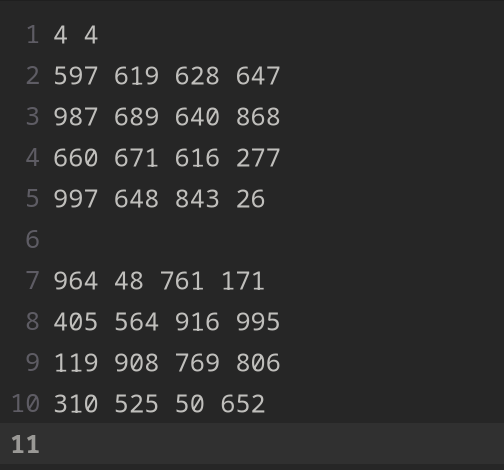
Fonte: Captura de tel feita pelo autor².
____________________________________________
²Captura de tela do computador do autor. Disponível em: Imagem 2.
Makefile: Controla a geração dos executáveis e compilação dos mesmos(FREE SOFTWARE FOUNDATION, GNU make, 2023).functions.cpp: Contém as funções criadas para execução nomain.cpp.structures.hpp: Contém as estruturas e chamadas de bibliotecas utilizadas no programa.main.cpp: Contém uma série de funções e declaração de variáveis que façam com que a busca pela matriz seja realizada devidamente.
A leitura das entradas do arquivo input.data são realizadas em 2 etapas, na primeira etapa é executada a função SizeRecon.
A função SizeRecon é responsável por ler a primeira linha do arquivo de entrada e retornar à alguma variável o valor de input.data.
Com input.data sejam alocados em uma variável. A estrutura do tipo MatrixElement nesse caso será uma matriz com variávies do tipo unsigned short int como elementos
Para a leitura das
Diante do que foi narrado, o programa recebe do usuário as coordenadas de
O programa usa
- As posições adjascentes correspondem à espaços da memória alocados pela matriz?
A validação citada ocorre através do seguinte modo:
- Criação de hipóteses dentro de variáveis booleanas,sendo o resultádo dessas variáveis é dependente da posição atual.As variáveis booleanas criadas tem os nomes de pontos cardeais em inglês, são elas W,SW,S,SE,E e podem ser verdadeiras ou falsas de maneiras diferentes tornando diversos caminhos possíveis.
Por fim pode-se abstrair a situação acima nas seguintes ilustrações, considerando que o elemento de cor laranja é o local atual:
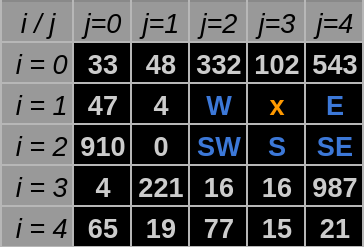
Fonte: Construção pelo autor³.
____________________________________________
³Criada usando o Google Sheets, Disponível em Planilha.
Após analisar as hipóteses, a decisão de qual é o melhor caminho a seguir é feita considerando o
Para buscar a maior direção válida, o programa decide quais são os pontos cardeais válidos, à depender disso ele executa uma das seguintes funções possíveis:
-
FivePossibleWays: Verifica qual o maior dentre 5 elementos, tendo uma posição de coordenadas
$i$ e$j$ diferentes da posição passada. Exemplo na Figura 4.
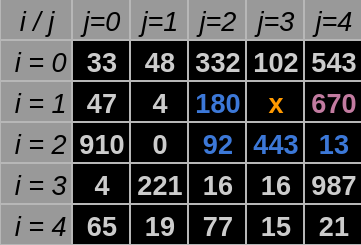
Fonte: Construção pelo autor⁴.
____________________________________________
⁴Criada usando o Google Sheets, Disponível em Planilha.
-
SouthEastPossibleWays: Verifica qual o maior dentre 3 elementos, tendo uma posição de coordenadas
$i$ e$j$ diferentes da posição passada. Estes elementos estão ao Sul, Leste ou Sudeste do$a_{ij}$ atual. Exemplo na Figura 5.
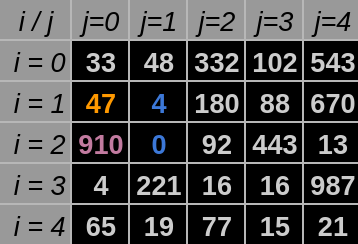
Fonte: Construção pelo autor⁵.
____________________________________________
⁵Criada usando o Google Sheets, Disponível em Planilha.
-
SouthWestPossibleWays: Verifica qual o maior dentre 3 elementos, tendo uma posição de coordenadas
$i$ e$j$ diferentes da posição passada. Estes elementos estão ao Sul, Oeste ou Sudoeste do$a_{ij}$ atual. Exemplo na Figura 6.
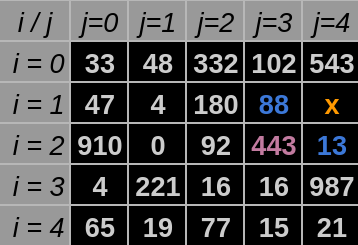
Fonte: Construção pelo autor⁶.
____________________________________________
⁶Criada usando o Google Sheets, Disponível em Planilha.
Existem alguns casos particulares onde teremos os seguintes movimentos:
- Quando a posição atual como
$a_{ij}$ tem seus valores de$i = N-1$ e$j =N-1 $ , ou seja, quando a posição atual for a última posição.Nesse caso a pesquisa na matriz é finalizada.
Figura 7 - Casa inicial ou presente é igual casa final.
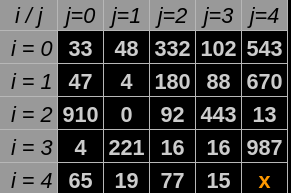
Fonte: Construção pelo autor⁷.
⁷Criada usando o Google Sheets, Disponível em Planilha.
- Quando a posição atual como
$a_{ij}$ tem seus valores de$i = N-1$ com$j$ sendo qualquer valor, ou seja, quando a posição atual está na última linha da matriz. Nesse caso o único movimento possível é avançando em colunas, ou seja de forma que o próximo passo tenha o$i$ constante e o$j=j+1$ até que se chegue à última casa. Isso acontece pelo fato de que ao chegar à última linha realizar um movimento que não siga essas diretrizes resultará na impossibilidade de continuar caminhando sem ter chegado ao final da matriz.
Figura 8 - Casa inicial ou presente tem
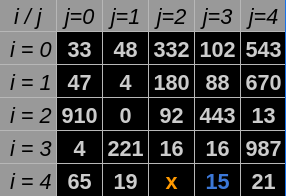
Fonte: Construção pelo autor⁸.
⁸Criada usando o Google Sheets, Disponível em Planilha.
-
Em casos de execução das funções: SouthWestPossibleWays, SouthEastPossibleWays ou FivePossibleWays onde os valores de duas ou mais casas adjascentes são iguais, haverá sempre preferência pelas casas adjascentes de maior valor na seguinte ordem:
- 1º Escolha do elemento com
$i = i+1$ e$j = j$ , ou seja, elemento abaixo. - 2º Escolha do elemento com
$i = i+1$ e$j = j+1$ , ou seja, elemento abaixo na diagonal direita. - 3º Escolha do elemento com
$i = i+1$ e$j = j$ , ou seja, à direita. - 4º Escolha do elemento com
$i = i+1$ e$j = j-1$ , ou seja, à direita.
- 1º Escolha do elemento com
Figura 9 - Casas adjascentes à inical com valor igual

Fonte: Construção pelo autor⁹.
⁹Criada usando o Google Sheets, Disponível em Planilha.
Em função de representar é realizado pelo algoritmo diante da entrada no arquivo input.data, observe as imagens abaixo. Considere que nas saídas, números diferentes de 999 repersentam a ordem da caminhada realizada, sendo 999 uma forma de representar localizações fora do trajeto:
Figura 10 - Entrada e saída de dados Matriz 1
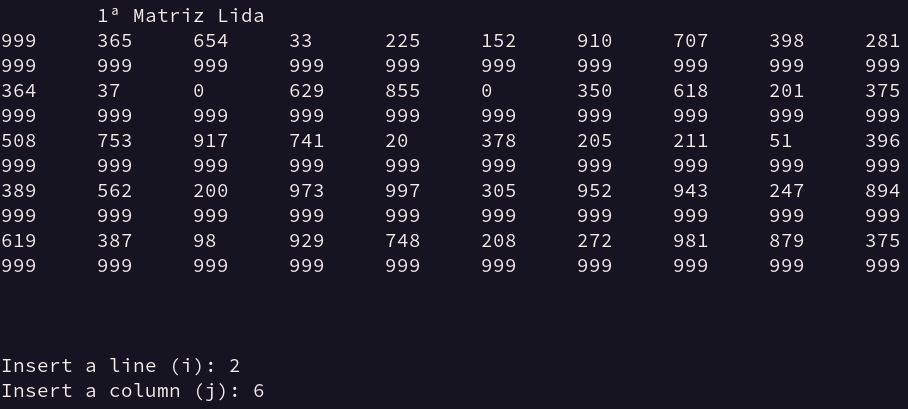
Figura 11 -
Saída de dados Matriz 1
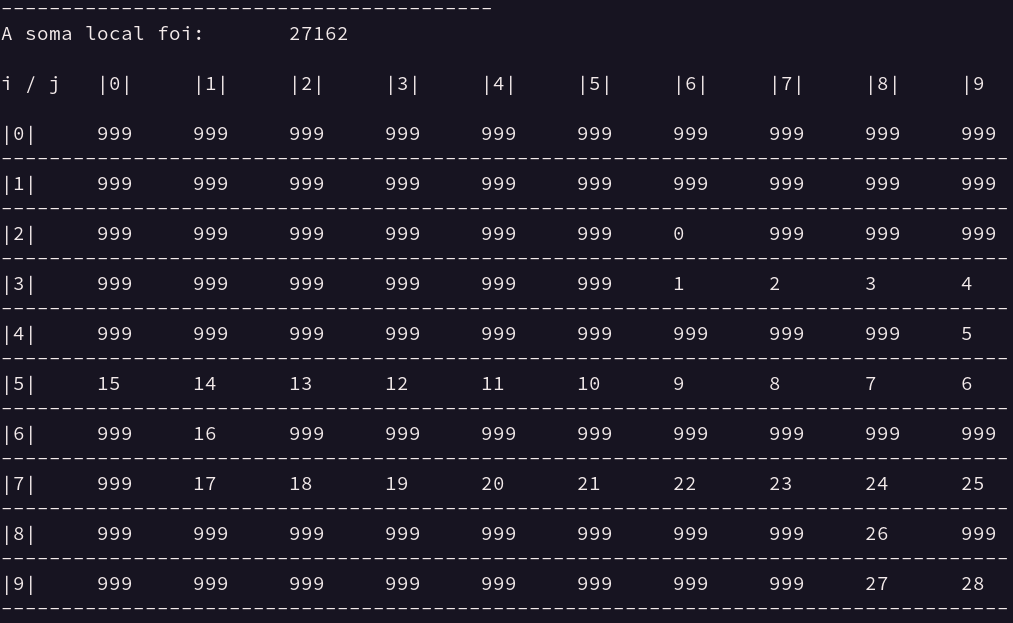
Figura 12 -
Entrada de dados Matriz 2
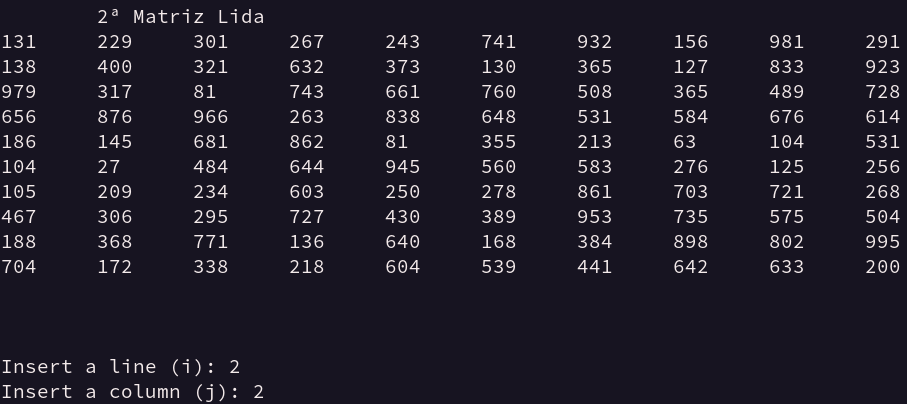
Figura 13 -
Saída de dados Matriz 2
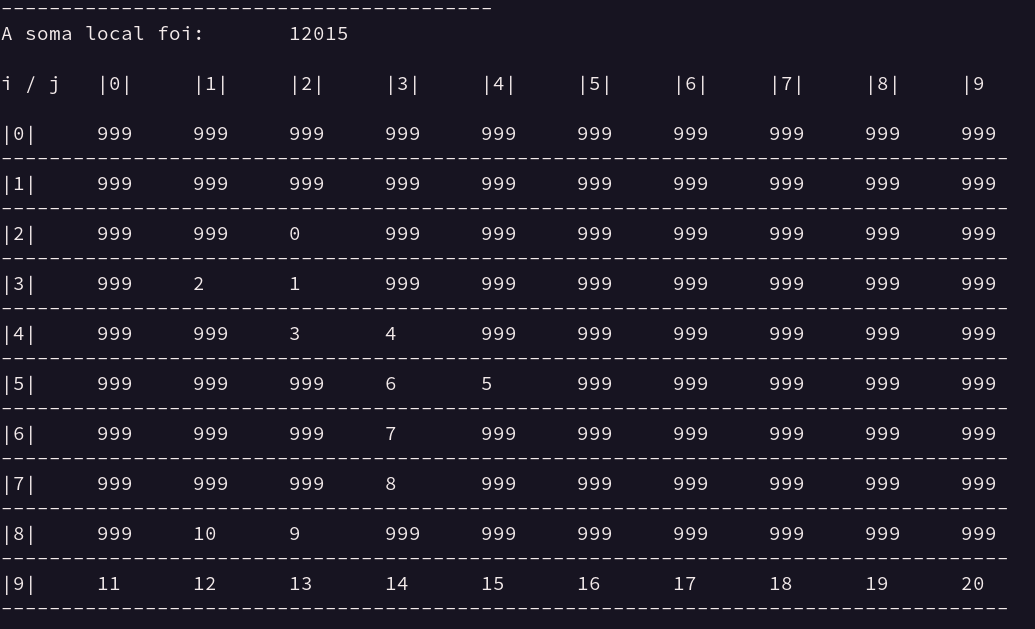
Figura 14 -
Saída de dados da Soma Global

Fonte: Captura de tela da compilação e execução realizada pelo autor ¹⁰.
¹⁰Criada Pela Compilação do código fonte(ordem de entradas: 2 e 6, 2 e 2), Disponível em Código Fonte.
"Um algoritmo guloso sempre faz a escolha que parece ser a melhor no momento em questão.
Isto é, faz uma escolha localmente ótima, na esperança de que essa escolha leve a uma solução globalmente ótima."
Algoritmos: teoria e prática, de Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest e Clifford Stein, tradução da 3ª edição
Com o intuito de preparar os alunos para a disciplina de Algoritmos e Estruturas de Dados dentro de um contexto onde os mesmos tivessem de ser avaliados em um período limitado de tempo, o desenvolvimento do desafio será avaliado diante da documentação e tentativa de construir um algoritmo guloso que resolvesse o problema apresentado.
Contudo, é importante ressaltar que a implementação de algoritmos gulosos necessita de um estudo aprofundado em outros cenários antes de ser implementado.
Considerando isso, são propostos por Cormen(2012) os Elementos da Estratégia Gulosa, ou seja, a projeção de algoritmos gulosos conta com a seguinte sequência de etapas:
- "Projetar o problema [...] como um problema no qual fazemos uma escolha e ficamos com um único subproblema para resolver"(CORMEN, 2012, p.354).
- "Provar que sempre existe uma solução ótima para o problema original que usa a escolha gulosa, de modo que a escolha gulosa é sempre segura"(CORMEN, 2012, p.354)."
- "Demonstrar subestrutura ótima, mostrando que, tendo feito a escolha gulosa, o que resta é o subproblema com a seguinte propriedade: se combinamos uma solução ótima para o subproblema com a escolha que fizemos, chegamos a uma solução ótima para o problema original"(CORMEN, 2012, p.354).
## Compilação e Execução Para compilação e execução do código é necessário que seja criado um arquivo Makefile. Para uso deste arquivo da forma correta, siga as diretrizes de execução abaixo:
| Comandos | Funções |
| make clean | Deleta o arquivo executável e todos os arquivos objetos do diretório. (FREE SOFTWARE FOUNDATION, GNU make, 2023) |
| make | Compila diferentes partes do programa através do g++ e cria um arquivo executável na pasta build. |
| make run | Executa o programa da pasta build após a realização da compilação. (PIRES, MICHEL, 2023) |
O código foi desenvolvido e testado no seguinte ambiente de desenvolvimento:
| Peças | Especificações |
| Processador | Intel(R) Core(TM) i5-3340M CPU @ 2.70GHz |
| Memória RAM | 8 GB |
| Sistema Operacional | Linux fedora 6.2.7-100.fc36.x86_64 |
[1] CORMEN, T. H. et al. Introduction to Algorithms, third edition. [s.l.] MIT Press, 2009. Acessador em 20 de Março de 2023.
[2] PIRES, MICHEL - Repositório GitHub, @mpiress: GenerateDataToMatrix - Disponível em: https://github.com/mpiress/GenerateDataToMatrix/blob/main/src/mat.h. Acessado em 15 de Março de 2023.
[3] GNU make. Disponível em: https://www.gnu.org/software/make/manual/make.html. Acessado em 21 de Março de 2023.
[4] GNU Make. Disponível em: https://www.gnu.org/software/make/. Acesso em: mar. 23DC.




