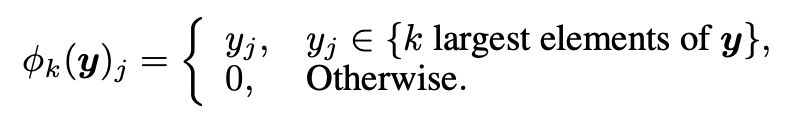This is the code for the paper "Enhancing Adversarial Defense by k-Winners-Take-All" by Chang Xiao, Peilin Zhong and Changxi Zheng (Columbia University).
- pytorch (1.0.0)
- torchvision (0.2.1)
- foolbox (1.9.0)
- numpy
- matplotlib
- tqdm
Winner-take-all (WTA) is a computational principle applied in computational models of neural networks by which neurons in a layer compete with each other for activation, which originated decades ago. k-WTA is a natural extension of WTA that retains the k largest values of an input vector and sets all others to be zero before feeding the vector to the next network layer, namely
The k-WTA operator can be used as an activation function to replace the popular activation functions such as ReLU in any of the modern deep networks, and this subsitiution can improves the robustness against gradient-based attacks while keep the standard accuracy, even without adversarial training. Note that this is the only change we propose to a deep neural network, and all other components (such as BatchNorm, convolution, pooling) remain unaltered.
This is a comparison between different activation functions that has a compete scheme. ReLU: all neurons with negative activation values will be set to zero. Max-pooling: only the largest activation in each group is transmitted to the next layer, and this effectively downsample the output. Local Winner-Takes-All (LWTA): the largest activation in each group retains its value when entering the next layer, others are set to zero. k-WTA: the k largest activations in the entire layer retain their values when entering the next layer, others are set to zero (k = 3 in this example). Note that the output is not downsampled through ReLU, LWTA and k-WTA.
An intriguing property of k-WTA is that it is discontinuous. We found that the discontinuities in k-WTA networks can largely prevent gradient-based search of adversarial examples and they at the same time remain innocuous to the network training.
This figure shows fitting a 1D function (green curve) using a k-WTA model provided with a set of points (red). The resulting model is piecewise continuous (blue), and the discontinuities can be dense. Notice that the gradient here cannot provide sufficient information for finding local minima of the model.
Here we show the effect of k-WTA activation on the loss landscape of a trained model.
We visualize the loss of a model with respect to its input on two directions, one is the direction of the loss gradient with respect to the input, another is a random direction. From left to right are ResNet+k-WTA, ResNet+k-WTA+Adversarial Training, ResNet+ReLU, ResNet+ReLU+Adversarial Training, respectively.
As shown in the figure, k-WTA models have a highly non-convex and non-smooth loss landscape. Thus, the estimated gradient is hardly useful for adversarial searches. This explains why k-WTA models can resist effectively gradient-based attacks. In contrast, ReLU models have a smooth loss surface, from which adversarial samples can be easily found using gradient descent.
The implementation of k-WTA can be found in kWTA/models.py. The forward pass of k-WTA can be implemented by a few lines in Pytorch:
def forward(self, x):
size = x.shape[1]*x.shape[2]*x.shape[3]
k = int(self.sr*size)
tmpx = x.view(x.shape[0], -1)
topval = tmpx.topk(k, dim=1)[0][:,-1]
topval = topval.repeat(tmpx.shape[1], 1).permute(1,0).view_as(x)
comp = (x>=topval).to(x)
return comp*xSee train-cifar.ipynb and train-svhn.ipynb
If you find this code helpful, please consider cite our paper
@article{xiao2019resisting,
title={Resisting Adversarial Attacks by $ k $-Winners-Take-All},
author={Xiao, Chang and Zhong, Peilin and Zheng, Changxi},
journal={arXiv preprint arXiv:1905.10510},
year={2019}
}
If you have any question on the code, please contact chang@cs.columbia.edu, enjoy!