These are intented to provide a beginner C++ programmer with hands-on examples of how to develop code within the OpenFOAM® framework. These tutorials hope to be more approachable than most of the materials available on-line, which tend to assume that the user is proficient in the C++ programming language. Please see below for a brief summary of what each individual tutorial covers and how to use it.
Current version of the tutorials is compatibile with the following OpenFOAM versions from the https://openfoam.org/ branch:
- OpenFOAM 5.x
- OpenFOAM 6 version 6
The "OldReleases" folder contains versions of the tutorials compatibile with past OpenFOAM versions, namely:
- OpenFOAM 3.0.1
Complete backwards compatibility has been dropped, however, and hence the older tutorials will be lacking in content (they should still all work though!).
There is a dedicated post on the CFD-online forum for discussing the tutorials, you're welcome to share your views and suggest new developments there: https://www.cfd-online.com/Forums/openfoam-community-contributions/188688-openfoam-programming-tutorials-beginners.html
It's advisable that you go through these basic C++ tutorials, having tried compiling and running most of the examples, before continuing: http://www.cplusplus.com/doc/tutorial/
Also, it's assumed you're familiar with running and setting up OpenFOAM® cases. If not, it's highly recommended you go through the official tutorials before you dive into the programming part: https://cfd.direct/openfoam/user-guide/tutorials/
Enjoy and please provide me with feedback to make these tutorials more useful! Contributions from the community are also more than welcome! Many thanks to the following people for offering their input:
- Chris Coutinho (cbcoutinho) for spotting errors in README and parallel processing tutorial
- Gerasimos Chourdakis (MakisH) for helping out with cleaning up the tutorial files
- Germilly Barreto (Germilly) for suggesting a tutorial on command line argument parsing
There is no set of notes or step-by-step set of instructions to follow in this offering of tutorials. Instead, each tutorial is a separate, stand-alone piece of code illustrating functionality of OpenFOAM from a programmer's perspective. They are, however, organised in an approximately increasing level of complexity so for new users it's advisable to make your way from start to finish. More experienced users, on the other hand, may wish to pick up bits and pieces here and there.
Each tutorial consists of code and a simple test case that demonstrates its
functionality. Most of the tutorials can be simply compiled with wmake and
the test case executed with Allrun. Deviations from this occur when compiling
libraries and hence compilation and clean-up Allwmake and Allwclean
scripts are contained in each tutorial directory to make their structure identical.
Therefore, to run each tutorial simply execute the following from its top-level
directory:
./Allwmake
cd testCase
./Allrun
There is also a testAll scripts that sequentially builds and tests each of
the tutorials while supressing all screen output. This is useful mostly for
checking version compatibility.
As there is no written narrative aside from the brief summaries below, all of the explanations are given in the form of comments in the code and in the test case control files, if necessary. Hence, the easiest way to use the tutorials effectively is to open up the source code, read it, use the comments to understand it, test it, and then tweak it to your liking.
Copyright by Artur K. Lidtke, 2017-2018.
This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM® software via www.openfoam.com, and owner of the OPENFOAM® and OpenCFD® trade marks.
Presents a basic OpenFOAM executable which prints a simple, yet important, message.
Shows how to read information from dictionaries and output it into files.
Shows how to pass arguments and options to custom applications.
Discusses how the OpenFOAM mesh description works and introduces the code interface used to interact with the grid.
Introduces the idea of a field object, reading values from OF-native files using built-in operators, as well as calculating field values by hand.
Gives a crash-course introduction to parallel computing with OpenFOAM and OpenMPI based on the example "solver" developed in Tutorial 4. The way OpenFOAM handles parallel domain decomposition is described, basic operators used for communication between parallel nodes are shown, and the basic solver is upgraded to work in parallel.
Shows how a new class may be added to expand OpenFOAM functionality, as well as gives an example implementation of a class derived from and OpenFOAM object. This is done by extending from the IOdictionary, with the aim of adding a custom method which lists the contents of the dict file, while keeping all of the baseline functionality.
Shows how an external library may be compiled and added to OpenFOAM. This is done by moving the key functionality of the "solver" from Tutorials 4 and 5 into an independent library, and then linking that against the rest of the solver code.
Shows how a custom boundary condition may be implemented. It does not introduce a bespoke utility, but instead only implements a library. This defines an inlet condition that allows a boundary layer profile to be prescribed at the inlet of a pipe.
The BC is implemented as a class derived from the fixedValue boundary condition, adding several control parameters allowing the inlet profile to be customised. Key elements of the code are highlighted with the keyword NOTE:. Key methods to pay attention to are the two constructors, default and one constructing the BC from string, and .updateCoeffs().
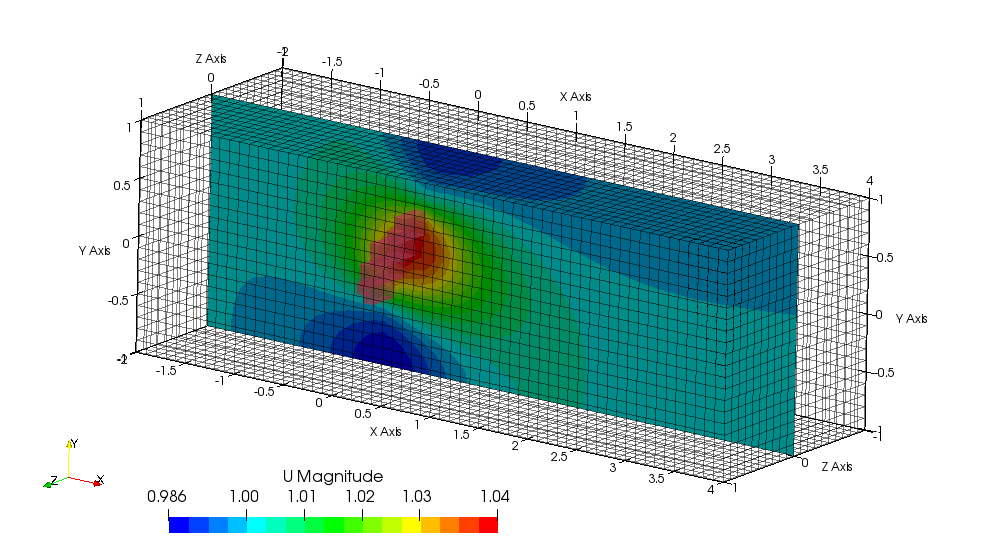
The test case is a straight pipe, flow through which gets solved with the basic simpleFoam solver. Key things to note are the definition of the BC in 0.org/U and the incorporation of a custom library in system/controlDict. The simulation is 3D RANS on a coarse mesh so it takes a few minutes on a low-end machine. The effect of the boundary condition may be visualised by plotting the x-velocity through the pipe and noting the incident boundary layer profile at the inlet and how it affects the solution.
Discusses the implementation of a a runtime post-processing utility which computes the flow rate through a face zone defined in the mesh using the topoSet utility.
The utility is implemented as a runtime postprocessing object derived from the built-in fvMeshFunctionObject and logFiles classes. It integrates the normal velocity through a specified face zone at each required time step and writes the result to a file, as well as prints in on the screen. The key methods to pay attention to are 1) the constructor 2) writeFileHeader(), 3) createFileNames(), and 4) write(), which implements the actual maths behind the functionality. Key elements of the code are highlighted with the keyword NOTE:. It is important to note that the utility gets compiled as a library, which then gets linked to the main solver, following the OpenFOAM runtime utility convention.
The test case is the same pipe as in Tutorial 8, except it uses a uniform inflow BC and is not run until full convergence. It is worth to note the definition of the faceZone of interest in system/topoSet. This may be visualised by selecting "Include zones" in paraview and applying the "Extract block" filter. As the simpleFoam solver is run, the output file gets created by the utility in the postProcessing directory.
Introduces the concepts behind solving a simple scalar transport equation.
The solver sets up the transport problem by importing a fixed velocity field from the last time step and solving the transport of a scalar, beta, in the presence of the velocity, beta being also subject to diffusion characterised by a fixed proportionality constant, gamma. The solver is conceptually similar to the built-in scalarTransportFoam, except it solves a steady-state problem. Key things to note are 1) the syntax behind the scalar transport equation 2) how OpenFOAM translates the syntax into specific operations and associates them with entries in system/fvSolution and system/fvSchemes dictionaries 3) inclusion of the boundary condition definitions in 0/beta into the equation 4) units of the equations being solved and how OpenFOAM handles them.
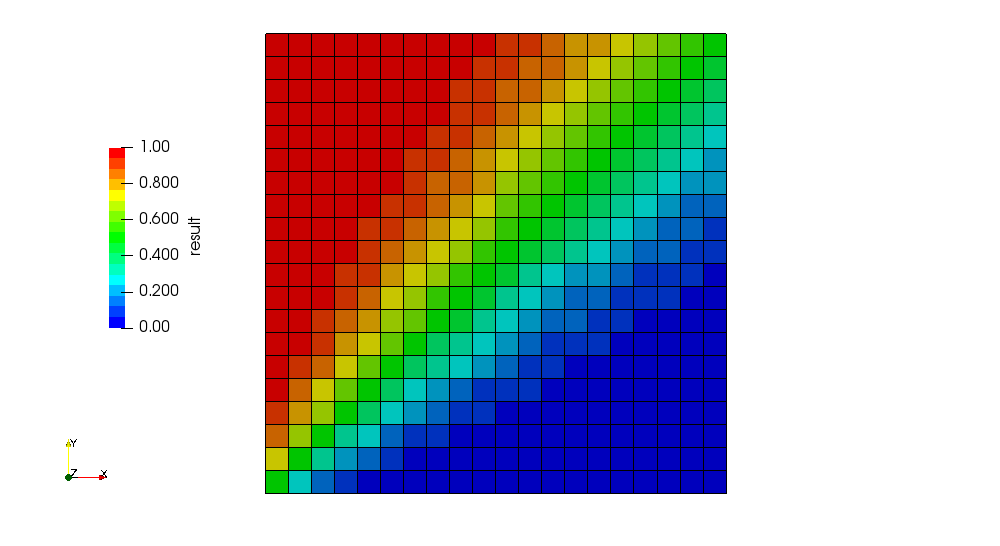
The test case is a simple 2D square domain with fixed scalar inlets at the bottom and the left-hand side. Transport takes place in the presence of a velocity field convecting away from the beta inlets. Once the case is run, it is best to visualise the initial conditions in the "beta" field and the solution to the transport equation saved as the "result" field.
Recommended reading:
- Wikipedia is always a good start:
https://en.wikipedia.org/wiki/Convection%E2%80%93diffusion_equation - Very brief description of the physical and mathematical concepts behind
the scalar transport equation by CFD-online:
https://www.cfd-online.com/Wiki/Generic_scalar_transport_equation - Chapters 3, 4 and especially 5 in "Numerical Methods in Heat, Mass,
and Momentum Transfer" by Murthy, J. Y. 2002:
https://engineering.purdue.edu/~scalo/menu/teaching/me608/ME608_Notes_Murthy.pdf
Demonstrates how to use points to generate different cell types, patches, and export the finished grid to an OpenFOAM case.
Also recommended to view the 'meshPoints.pdf' or Gmsh files to get a better idea of how the mesh is actually constructed from points.
Shows a modified version of the actuatorDisk momentum source which does not use a cellSet in order to mark cells for applying the source. Instead, it identifies the cells inside of the constructor which allows easier adjustment of the disk parameters and could be developed further to include a dynamic variant. Main part of the implementation is located in "customActuationDiskSourceTemplates.C" and the cell selection algorithm is implemented in the class constructor inside "customActuationDiskSource.C". Key takeaways from the tutorial are how a fvOption object is structured and how it may be modified to suit ones needs. It is a bit more applied than the previous ones but hopefully will be useful to at least a few people.