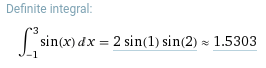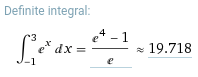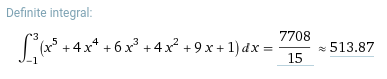jakubowiczish/fortran-task3

My solution for Fortran assignment - task 3

Fortran task 3 - Integration using coarrays

Source files

There are 4 source files in src directory:

• main.F90 - contains major part of the project
• rectangular_integration.F90 - rectangular integration interface
• trapezoidal_rule_integration.F90 - trapezoidal rule integration interface
• testing_function.F90 - contains exemplary functions that are integrated in main.F90
• I did not do the part of the task with Gaussian integration

Running instruction

1. Clone repository
2. Go to src directory
3. Type make run in terminal
   • Results will be printed on standard output.
   • Results will be also stored in additional file: integration_results.txt in res directory

There might be several warnings like:

[0] MPI startup(): I_MPI_SCALABLE_OPTIMIZATION environment variable is not supported.
[0] MPI startup(): I_MPI_JOB_CONTEXT environment variable is not supported.
[0] MPI startup(): Similar variables:
	 I_MPI_HYDRA_PMI_CONNECT
[0] MPI startup(): I_MPI_DEVICE environment variable is not supported.
[0] MPI startup(): Similar variables:
	 I_MPI_ADJUST_REDUCE
[0] MPI startup(): I_MPI_FALLBACK environment variable is not supported.
[0] MPI startup(): I_MPI_CAF_RUNTIME environment variable is not supported.
[0] MPI startup(): Similar variables:
	 I_MPI_THREAD_RUNTIME
[0] MPI startup(): To check the list of supported variables, use the impi_info utility or refer to https://software.intel.com/en-us/mpi-library/documentation/get-started.

Results and conclusions

Everything works fine, results are presented for small intervals like integrating from -1.0 to 3.0.

For larger intervals there were huge gaps between real result and result calculated by those 2 methods.

All results are available in integration_results.txt in res directory

I used wolfram alpha in order to show you that the results are quite correct:

1. Result for integrating y = sin(x)

• Using trapezoidal rule: 1.55694762674353
• Using rectangular rule: 1.54635237758489
• Using Wolfram Alpha:

2. Result for integrating y = e^x

• Using trapezoidal rule: 20.1267405355118
• Using rectangular rule: 19.5137530615636
• Using Wolfram Alpha:

3. Result for integrating y = x**5 + 4 * x**4 + 6 * x**3 + 4 * x**2 + 9 * x + 1

• Using trapezoidal rule: 535.125000000000
• Using rectangular rule: 503.265625000000
• Using Wolfram Alpha:

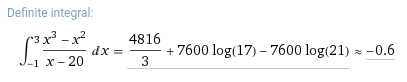
4. Result for integrating y = (x**3 - x**2) / (x - 20)

• Using trapezoidal rule: -0.637918548248534
• Using rectangular rule: -0.604718665448629
• Using Wolfram Alpha:

Results might differ from one another because of the method used and because of number of images