Neural Rough Differential Equations for Long Time Series
(ICML 2021)
[arXiv]

Overview

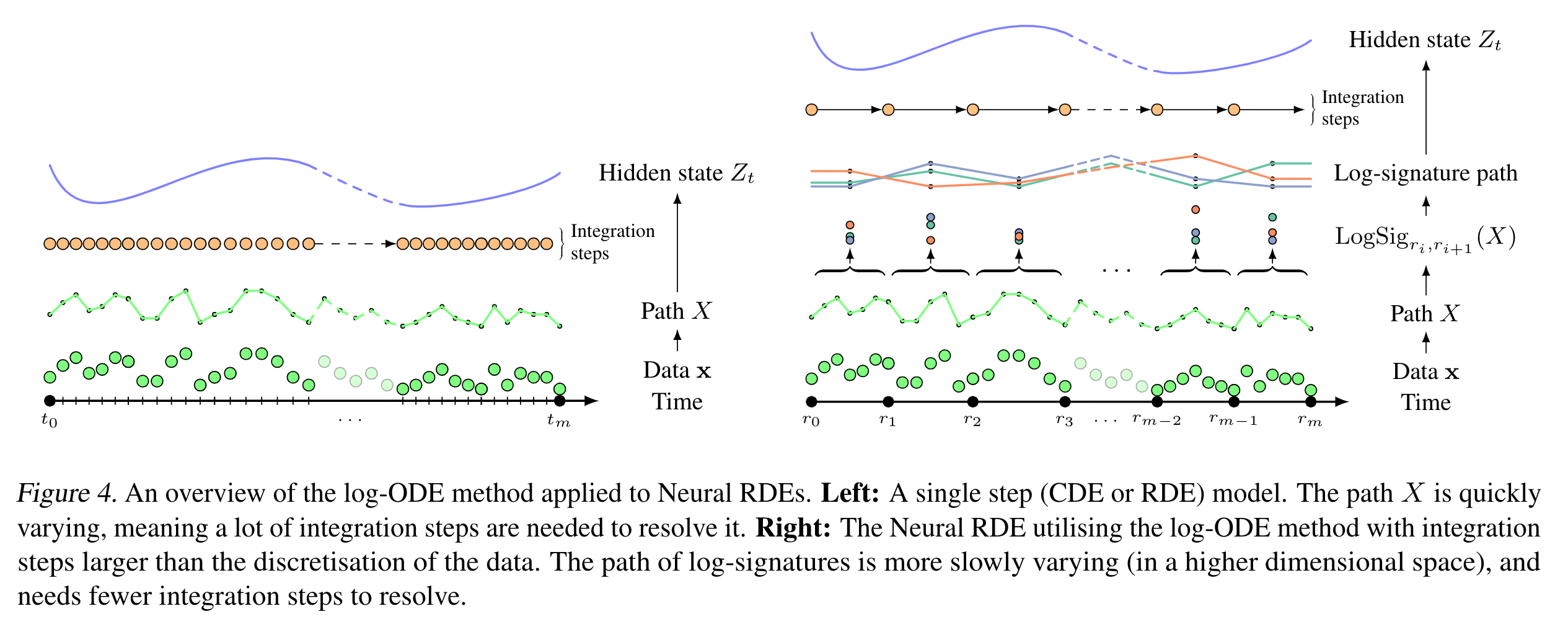
Neural Controlled Differential Equations (Neural CDEs) are the continuous-time analogue of an RNN. However, as with RNNs, training can quickly become impractical for long time series. Here we use rough path theory to extend this formulation through application of a pre-existing mathematical tool from rough analysis - the log-ODE method - which allows us to take integration steps larger than the discretisation of the data, resulting in significantly faster training times, with retainment (and often even improvements) in model performance.

Loosely speaking, this corresponds to binning the data prior to running a Neural CDE, with bin statistics carefully chosen to extract precisely the information most relevant to solving a CDE. We have traded in length for additional input channels, with this trade off coming at the cost of having two additional hyperparameters to tune.

Paper

This repository contains all the code for reproducing the experiments from the Neural Rough Differential Equations for Long Time Series paper.

Code

Code for constructing the log-signature NCDEs is in the ncdes/ folder and can be adapted to run your own models.

Library

We recommended checking out the torchcde project, which is a well maintained library for doing all things NCDE related, and now includes a log-ODE implementation.

Reproducing the Experiments

Setup the Environment

First to setup the environment, install the requirements with

pip install -r requirements.txt
pip install signatory==1.2.0.1.4.0 --no-cache-dir --force-reinstall

(Signatory has to be installed after PyTorch, due to limitations with pip).

Downloading the Data

Now setup a folder to save the data in at data/raw/. Here data/ should be made a symlink if you do not want to store the data in the project root.

Navigate into get_data/ and run

python get_data/uea.py
python get_data/tsr.py This will download the EigenWorms and BIDMC data to data/raw/ that was used in the paper (note that this can take a couple of hours as it downloads the entire UEA and TSR archives).

Run the Experiments

Finally, run the experiments. We provide a convenient script experiments/runs.py for doing this. Note that we need to run a hyperparameter optimization search and then the main run for each dataset. To run a hyperoptimzation followed and then the main experiment run navigate into experiments, open python and run

>>> import runs
>>> runs.run('UEA', 'EigenWorms', 'hyperopt')   # Syntax is run(dataset_folder, dataset_name, configuration_name)
# Once completed
>>> runs.run('UEA', 'EigenWorms', 'main')

This being an example for EigenWorms. For the BIDMC data it is just:

>>> import runs
>>> runs.run('TSR', 'BIDMC32{*}', 'hyperopt')   # Where {*} is one of {RR, HR, SpO2}
>>> runs.run('TSR', 'BIDM32{*}', 'main')

This will run on the cpu. If you have GPUs available and wish to run on the GPU (strongly recommended) we have an optional gpu_idxs argument that takes a list of gpu indexes. For example,

>>> runs.run('TSR', 'BIDM32RR', 'main', gpu_idxs=[0, 1])

will run the respiration rate runs on GPUs with indexes [0, 1].

We do have an option to run all the runs in one go

>>> runs.run(gpu_idxs=[0, 1])    # With user specified GPUs

but this is not recommended as it may take ~1-2 weeks.

Analysis of Results

Results will be saved to experiments/models/. To properly analyse them we recommend opening them in a jupyter notebook (see notebooks/{results, plots}.ipynb to reproduce the tables and figures from the paper), however for an overview one can use the parse_results.py file in experiments/ by running the following in the terminal

> python parse_results.py TSR BIDMC32RR hyperopt    # Arguments are the same as the runs.run function

this will print an overview of the results to the console.

Citation

@article{morrill2021neuralrough,
  title={Neural Rough Differential Equations for Long Time Series},
  author={Morrill, James and Salvi, Cristopher and Kidger, Patrick and Foster, James and Lyons, Terry},
  journal={International Conference on Machine Learning},
  year={2021}
}

jambo6/neuralRDEs

Neural Rough Differential Equations for Long Time Series (ICML 2021) [arXiv]