The code is present in the Code folder.
- kmeans.py : Python implementation of the Lloyd's Algorithm [1]
- heuristic_kmeans.py : Python implementation of Lloyd's Algorithm [1] augmented with our heuristic
- triangleInequality.py : Python implementation of the K-means with Triangle Inequality Algorithm [2]
- heuristic_triangleinequality.py : Python implementation of the K-means with Triangle Inequality Algorithm [2] augmented with our heuristic
- enhancedKmeans.py : Python implementation of Enhanced K-means algorithm [4]
- heuristic_enhancedKmeans.py : Python implementation of Enhanced K-means algorithm [4] augmented with our heuristic
- kpp.py : Python implementation of K-means++ [3] algorithm. As this is only a seeding technique, it can be used with any other K-means algorithm (including the ones mentioned above). Therefore, a separate augmentation with our heuristic is not provided.
The datasets used in our paper are present in the Datasets folder.
There are three types of files:
- Seeding Algorithms (kpp.py)
- Algorithms not augmented with our heuristic.
- Algorithms augmented with our heuristic
A sample code for running kpp.py is given below
kplus = KPP(numClusters,X=np.array(pointList))
kplus.init_centers()
cList = [Point(x,len(x)) for x in kplus.mu]If the code for an algorithm not augmented with our heuristic, it can be run by calling the following function
Kmeans(k, pointList, kmeansThreshold, initialCentroids=None)
# k = Number of Clusters
# pointList = List of n-dimensional points (Every point should be a list)
# kmeansThreshold = Percentage Change in Mean Squared Error (MSE) below which the algorithm should stop. Used as a stopping criteria
# initialCentroids (optional) = Provide initial seeds for centroids (List of Point() class objects). It can be generated from a list of n-dimensional points as follows:
# initialCentroids = [Point(x,len(x)) for x in pointList]If the code for an algorithm augmented with our heuristic, it can be run by calling the following function
Kmeans(k, pointList, kmeansThreshold, centroidsToRemember, initialCentroids=None)
# k = Number of Clusters
# pointList = List of n-dimensional points (Every point should be a list)
# kmeansThreshold = Percentage Change in Mean Squared Error (MSE) below which the algorithm should stop. Used as a stopping criteria
# centroidsToRemember = The value of k'. This value is the percentage of k to be used as the Candidate Cluster List (CCL)
# initialCentroids (optional) = Provide initial seeds for centroids (List of Point() class objects). It can be generated from a list of n-dimensional points as follows:
# initialCentroids = [Point(x,len(x)) for x in pointList]Major bottleneck of K-means clustering is the computation of data point to cluster centroid distance. For a dataset with n data points and k clusters, each iteration of K-means performs n x k such distance computations. To overcome this bottleneck, we maintain a list of candidate clusters for each data point. Let size of this list be k'. We assume that k' is significantly smaller than k. We build this candidate cluster list based on top k' nearest clusters to the data point after first iteration of K-means. Now each iteration of K-means will perform only n x k' distance computations.
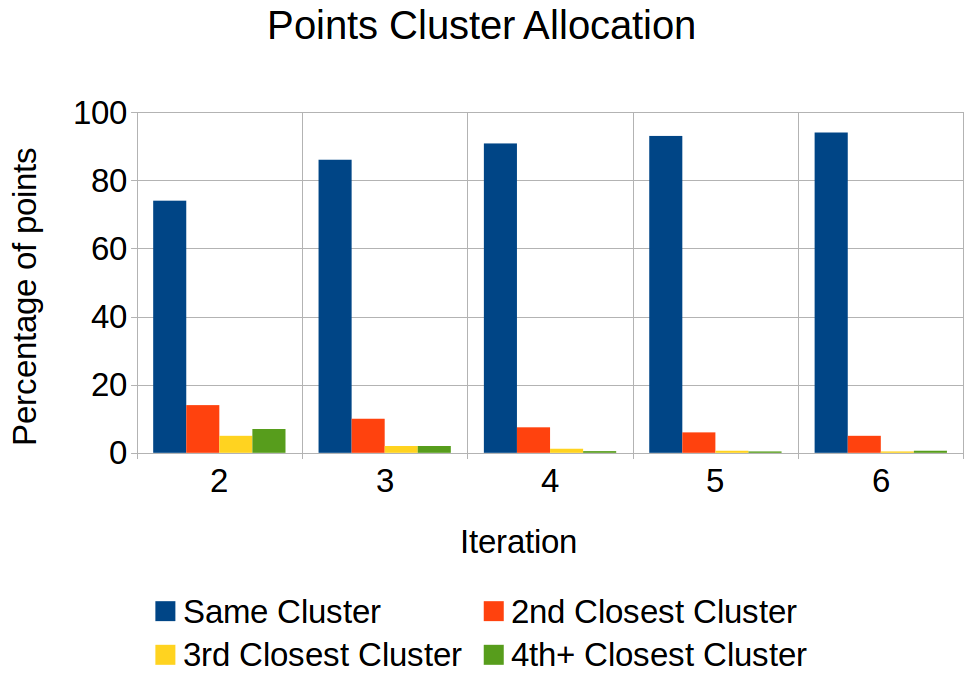
Motivation for this approach comes from the observation that data points have tendency to go to clusters that were closer in the previous iteration. In k-means, we compute distance of a data point to every cluster even though the point has extremely little chance of being assigned to it. The figure below shows an example execution of k-means for a synthetic dataset of 100,000 points in 10 dimensions which needs to be partitioned into 100 clusters. X axis represents iteration of the algorithm and Y axis represents percentage of points that get assigned to a particular cluster. For example, in iteration 2, about 75 percent points got reassigned to same cluster as in iteration 1 and about 10 percent points got assigned to a cluster that was second closest cluster in previous iteration. As we progress through the algorithm, more points get assigned to same cluster or clusters that were close in previous iteration.
Experimental results are presented on five datasets, four of which were used by Elkan et. al.[2] to demonstrate the effectiveness of K-Means with Triangle Inequality and one is a synthetically generated dataset by us. These datasets vary in dimensionality from 2 to 784, indicating applicability of our heuristic for low as well as high dimensional data.
Let algorithm V be a variant of k-means and algorithm V' be the same variant augmented with our heuristic. Let T be the time required for V to converge to MSE value of E. Similarly, T' is the time required for V' to converge to MSE value of E'.
Our evaluation metrics are the following:
- Speedup : Calulated as
(T/T'). - Percentage increase in MSE (PIM) : Calculated as
100 * (E' - E)/E.
| k' = 20 | k' = 30 | k' = 40 | k' = 50 | k' = 60 | ||
|---|---|---|---|---|---|---|
| Birch | PIM % | 0.01 | 0 | 0 | 0 | 0 |
| Speedup | 3.68 | 2.78 | 2.12 | 1.75 | 1.53 | |
| Mnist | PIM % | 0.77 | 0.41 | 0.21 | 0.25 | 0.13 |
| Speedup | 3.97 | 3.29 | 3.03 | 2.13 | 1.4 | |
| KDDCup | PIM % | 0.2 | 0.07 | 0.18 | 0 | 0 |
| Speedup | 9.47 | 3.18 | 4.07 | 1.46 | 1.22 | |
| Synthetic | PIM % | 0.19 | 0.11 | 0.06 | 0.04 | 0.01 |
| Speedup | 8.48 | 4.37 | 2.27 | 2.49 | 1.38 |
| k' = 20 | k' = 30 | k' = 40 | k' = 50 | k' = 60 | ||
|---|---|---|---|---|---|---|
| Birch | PIM % | -0.11 | 0.04 | 0 | 0 | 0 |
| Speedup | 3.05 | 2.48 | 2.01 | 1.68 | 1.41 | |
| Covtype | PIM % | 0.21 | 0.02 | 0 | 0 | 0 |
| Speedup | 2.32 | 1.81 | 1.61 | 1.55 | 1.42 | |
| Mnist | PIM % | 1.30 | 0.72 | 0.51 | 0.43 | 0.37 |
| Speedup | 1.90 | 1.68 | 1.59 | 1.48 | 1.47 | |
| KDDCup | PIM % | 0.81 | 0.11 | 0.08 | -0.18 | 0 |
| Speedup | 1.44 | 1.33 | 1.42 | 0.88 | 1.18 | |
| Synthetic | PIM % | 0.19 | 0.11 | 0.06 | 0.03 | 0.01 |
| Speedup | 2.90 | 2.28 | 1.87 | 1.51 | 1.36 |
Note that as K-means++ is just a seeding technique, K-means with Triangle Inequality is used as the algorithm after seeding
| k' = 20 | k' = 30 | k' = 40 | k' = 50 | k' = 60 | ||
|---|---|---|---|---|---|---|
| Birch | PIM % | 0 | 0 | 0 | 0 | 0 |
| Speedup | 3.14 | 2.26 | 1.93 | 1.67 | 1.31 | |
| Covtype | PIM % | 0.03 | 0 | 0 | 0 | 0 |
| Speedup | 2.02 | 1.82 | 1.63 | 1.38 | 1.20 | |
| Mnist | PIM % | 1.36 | 0.71 | 0.36 | 0.18 | 0.09 |
| Speedup | 1.47 | 1.44 | 1.26 | 1.19 | 1.15 | |
| KDDCup | PIM % | 0.70 | 0.15 | 0.02 | -0.01 | 0 |
| Speedup | 1.60 | 1.15 | 1.02 | 0.99 | 1.02 | |
| Synthetic | PIM % | 0.15 | 0.08 | 0.04 | 0.01 | 0.01 |
| Speedup | 2.45 | 1.97 | 1.71 | 1.35 | 1.17 |
| k' = 20 | k' = 30 | k' = 40 | k' = 50 | k' = 60 | ||
|---|---|---|---|---|---|---|
| Birch | PIM % | 0.002 | 0 | 0 | 0 | 0 |
| Speedup | 2.04 | 1.87 | 1.57 | 1.39 | 1.26 | |
| Covtype | PIM % | -0.01 | 0 | 0 | 0 | 0 |
| Speedup | 2.86 | 2.28 | 1.88 | 1.59 | 1.38 | |
| Mnist | PIM % | 0.83 | 0.40 | 0.22 | 0.12 | 0.05 |
| Speedup | 4.76 | 3.32 | 2.25 | 1.63 | 1.40 | |
| KDDCup | PIM % | 0.006 | 0.004 | 0 | 0 | 0 |
| Speedup | 3.37 | 3.04 | 2.27 | 1.80 | 1.57 |
[1] S. P. Lloyd. Least squares quantization in pcm. Information Theory, IEEE Trans. on, 28(2):129–137, 1982.
[2] C. Elkan. Using the triangle inequality to accelerate k-means. In International Conference on Machine Learning, pages 147–153, 2003.
[3] D. Arthur and S. Vassilvitskii. k-means++: The advantages of careful seeding. InACM-SIAM symposium on Discrete algorithms, pages 1027–1035, 2007.
[4] Fahim, A. M., et al. An efficient enhanced k-means clustering algorithm. Journal of Zhejiang University-Science A 7.10 (2006): 1626-1633.