Distributional Compositional Python

DisCoPy is a tool box for computing with monoidal categories.

Features

Diagrams & Recipes

Diagrams are the core data structure of DisCoPy, they are generated by the following grammar:

diagram ::= Box(name, dom=type, cod=type)
    | diagram @ diagram
    | diagram >> diagram
    | Id(type)

type ::= Ty(name) | type.l | type.r | type @ type | Ty()

String diagrams (also known as tensor networks or Penrose notation) are a graphical calculus for computing with monoidal categories. For example, if we take ingredients as types and cooking steps as boxes then a diagram is a recipe:

from discopy import Ty, Box, Id, Swap

egg, white, yolk = Ty('egg'), Ty('white'), Ty('yolk')
crack = Box('crack', egg, white @ yolk)
merge = lambda x: Box('merge', x @ x, x)

crack_two_eggs = crack @ crack\
    >> Id(white) @ Swap(yolk, white) @ Id(yolk)\
    >> merge(white) @ merge(yolk)
crack_two_eggs.draw(path='docs/_static/imgs/crack-eggs.png')

Snakes & Sentences

Wires can be bended using two special kinds of boxes: cups and caps, which satisfy the snake equations, also called triangle identities.

from discopy import Cup, Cap

x = Ty('x')
left_snake = Id(x) @ Cap(x.r, x) >> Cup(x, x.r) @ Id(x)
right_snake =  Cap(x, x.l) @ Id(x) >> Id(x) @ Cup(x.l, x)
assert left_snake.normal_form() == Id(x) == right_snake.normal_form()

In particular, DisCoPy can draw the grammatical structure of natural language sentences encoded as reductions in a pregroup grammar (see Lambek, From Word To Sentence (2008) for an introduction).

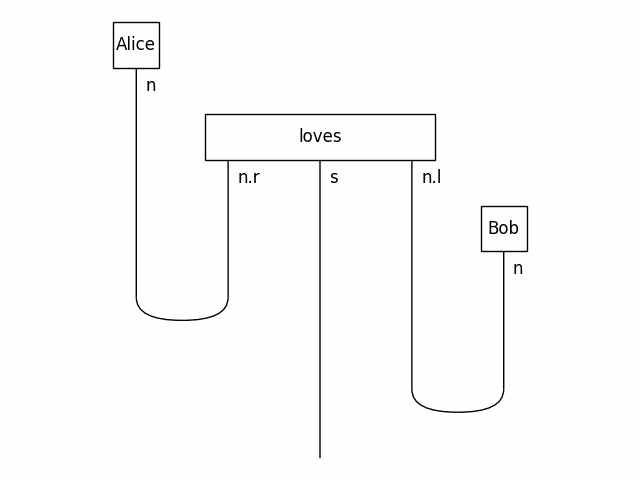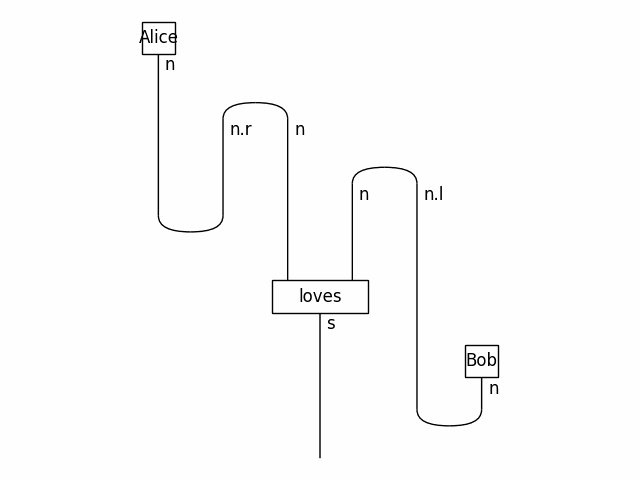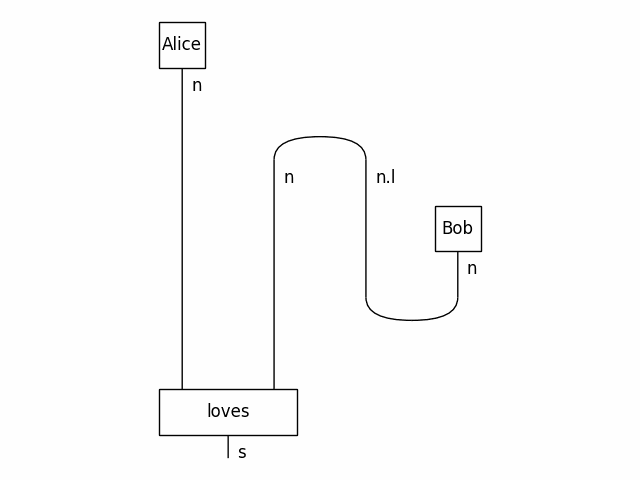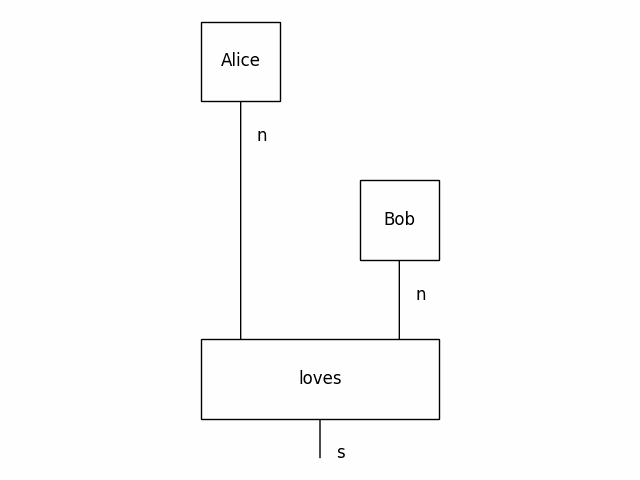
from discopy import pregroup, Word

s, n = Ty('s'), Ty('n')
Alice, Bob = Word('Alice', n), Word('Bob', n)
loves = Word('loves', n.r @ s @ n.l)

sentence = Alice @ loves @ Bob >> Cup(n, n.r) @ Id(s) @ Cup(n.l, n)
pregroup.draw(sentence, path='docs/_static/imgs/alice-loves-bob.png')

Functors & Rewrites

Monoidal functors compute the meaning of a diagram, given an interpretation for each wire and for each box. In particular, tensor functors evaluate a diagram as a tensor network using numpy. Applied to pregroup diagrams, DisCoPy implements the distributional compositional (DisCo) models of Clark, Coecke, Sadrzadeh (2008).

from discopy import TensorFunctor

F = TensorFunctor(
    ob={s: 1, n: 2},
    ar={Alice: [1, 0], loves: [[0, 1], [1, 0]], Bob: [0, 1]})

assert F(sentence) == 1

Free functors (i.e. from diagrams to diagrams) can fill each box with a complex diagram. The result can then be simplified using diagram.normalize() to remove the snakes.

from discopy import Functor

def wiring(word):
    if word.cod == n:  # word is a noun
        return word
    if word.cod == n.r @ s @ n.l:  # word is a transitive verb
        return Cap(n.r, n) @ Cap(n, n.l)\
            >> Id(n.r) @ Box(word.name, n @ n, s) @ Id(n.l)

W = Functor(ob={s: s, n: n}, ar=wiring)


rewrite_steps = W(sentence).normalize()
sentence.to_gif(*rewrite_steps, path='autonomisation.gif', timestep=1000)

Getting Started

pip install discopy

Contributing

Contributions are welcome, please drop one of us an email or open an issue.

Tests

If you want the bleeding edge, you can install DisCoPy locally:

git clone https://github.com/oxford-quantum-group/discopy.git
cd discopy
pip install .

You should check you haven't broken anything by running the test suite:

pip install ".[test]" .
pip install pytest coverage pycodestyle
coverage run -m pytest --doctest-modules --pycodestyle
coverage report -m discopy/*.py discopy/*/*.py

The documentation is built automatically from the source code using sphinx. If you need to build it locally, just run: