The CMA Evolution Strategy is a stochastic method for derivative-free optimization of potentially non-linear, non-convex or noisy functions over continuous domains (Hansen 2016). A brief discussion of its performance in practice can be found on wikipedia.
The default settings and implementation details follow closely Hansen 2016 and pycma.
julia> function rosenbrock(x)
n = length(x)
sum(100 * (x[2i-1]^2 - x[2i])^2 + (x[2i-1] - 1)^2 for i in 1:div(n, 2))
end
julia> using CMAEvolutionStrategy
julia> result = minimize(rosenbrock, zeros(6), 1.)
(4_w,9)-aCMA-ES (mu_w=2.8,w_1=49%) in dimension 6 (seed=17743412058849885570, 2020-05-12T16:22:27.211)
iter fevals function value sigma time[s]
1 9 6.06282462e+02 8.36e-01 0.008
2 18 6.00709117e+02 8.42e-01 0.009
3 27 2.40853796e+02 7.84e-01 0.009
100 900 8.25748973e-01 1.44e-01 0.021
200 1800 2.21358637e-05 1.12e-02 0.040
266 2394 5.58767672e-12 2.76e-05 0.051
Optimizer{Parameters,BasicLogger,Stop}
(4_w,9)-aCMA-ES (mu_w=2.8,w_1=49%) in dimension 6 (seed=17743412058849885570, 2020-05-12T16:22:27.254)
termination reason: ftol = 1.0e-11 (2020-05-12T16:22:27.255)
lowest observed function value: 1.076905008476142e-12 at [0.9999990479016964, 0.9999981609497738, 0.9999990365312236, 0.9999981369588251, 0.9999994689450983, 0.9999988356249463]
population mean: [1.000000255106133, 1.0000004709845969, 1.0000006232562606, 1.0000012290059055, 0.9999998790530266, 0.9999997338544545]
julia> xbest(result)
6-element Array{Float64,1}:
0.9999990479016964
0.9999981609497738
0.9999990365312236
0.9999981369588251
0.9999994689450983
0.9999988356249463
julia> fbest(result)
1.076905008476142e-12
julia> population_mean(result)
6-element Array{Float64,1}:
1.000000255106133
1.0000004709845969
1.0000006232562606
1.0000012290059055
0.9999998790530266
0.9999997338544545
help?> minimize
search: minimize
minimize(f, x0, s0;
lower = nothing,
upper = nothing,
constraints = _constraints(lower, upper),
noise_handling = nothing,
popsize = 4 + floor(Int, 3*log(length(x0))),
callback = (object, inputs, function_values, ranks) -> nothing,
parallel_evaluation = false,
multi_threading = false,
verbosity = 1,
seed = rand(UInt),
logger = BasicLogger(x0, verbosity = verbosity, callback = callback),
maxtime = nothing,
maxiter = nothing,
maxfevals = nothing,
stagnation = 100 + 100 * length(x0)^1.5/popsize,
ftarget = nothing,
xtol = nothing,
ftol = 1e-11)
Minimize function f starting around x0 with initial covariance s0 * I under box constraints
lower .<= x0 .<= upper, where x0, lower and upper are vectors of the same length or
nothing.
The result is an Optimizer object from which e.g. xbest, fbest or population_mean can be
extracted.
If parallel_evaluation = true, the objective function f receives matrices of n rows (n =
length(x0)) and popsize columns and should return a vector of length popsize. To use
multi-threaded parallel evaluation of the objective function, set multi_threading = true
and start julia with multiple threads (c.f. julia manual for the multi-threading
setup).The standard settings may work well for noisy objective functions. To avoid
premature convergence due to too fast decrease of sigma, there is the option
noise_handling = CMAEvolutionStrategy.NoiseHandling(ασ = 1.1, callback = s -> s > 0).
Choose ασ such that sigma decreases slowly (and does not diverge). The callback
function can be used to change the objective function, e.g. increase the
measurement duration, if this leads to smaller noise. The variable s indicates
whether CMA-ES can handle the current level of noise: s > 0 indicates that the
noise level is too high. Whenever the callback returns true, sigma gets multiplied by
ασ, which is the case when s > 0, with the default callback.
For details on noise handling see Hansen 2009.
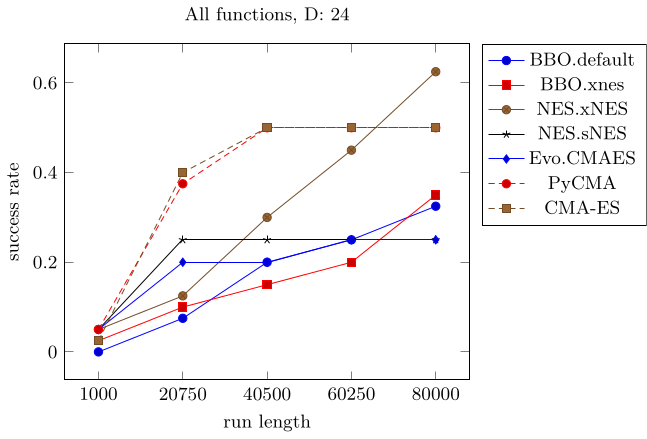
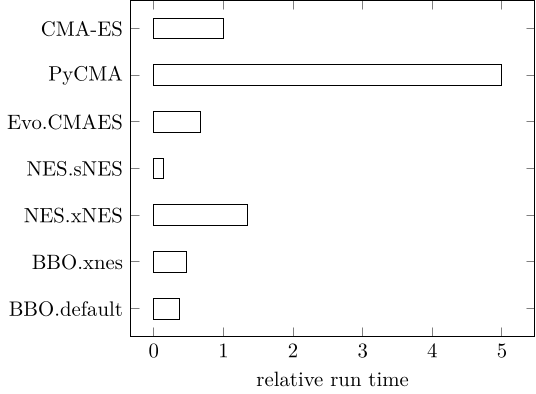
Running BlackBoxOptimizationBenchmarking in 24 dimensions, highlights the advantage of CMA-ES early in optimization. All methods were chained into NelderMead after 90% of the run length (c.f. BlackBoxOptimizationBenchmarking)
CMAES = this package, BBO = BlackBoxOptim, NES = NaturalES, Evo = Evolutionary, PyCMA = pycma