A R package for functional data analysis using the square root velocity framework which performs pair-wise and group-wise alignment as well as modeling using functional component analysis
v2.3.2 is on CRAN and can be installed as
install.packages("fdasrvf")`For a more up to date, but may not be stable version from git repository.
- Download zip or tar.gz of package or clone repository
- Install into R (> 4.3.0)
library(devtools)
install_github("jdtuck/fdasrvf_R")The package contains simu dataset that is handy to experiment with the
available functions for functions in
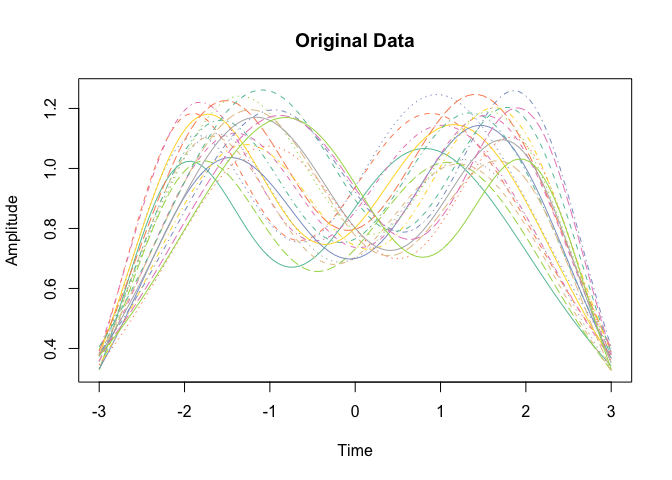
We first visualize this dataset:
For that we first turn on class of functions present in the f for
visualization:
library(fdasrvf)
f_plot(simu_data$time, simu_data$f)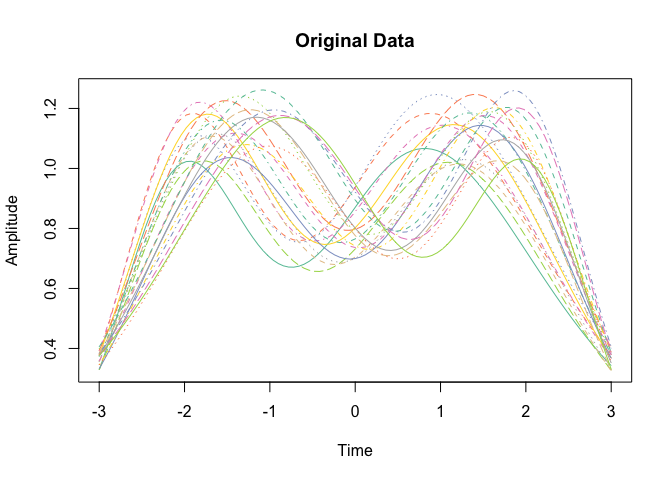 We can
see that each
We can
see that each curve is a functionally closed 2D curve. And we
distinguish different patterns of miss-alignment, like X values
shrinking, small displacement, and many others.
We will now proceed with curve alignment for the curves of this class 1:
obj <- time_warping(simu_data$f, simu_data$time)
#> ℹ Using lambda = 0
#> ℹ Initializing...
#> ℹ Computing Karcher mean of 21 functions in SRSF space...
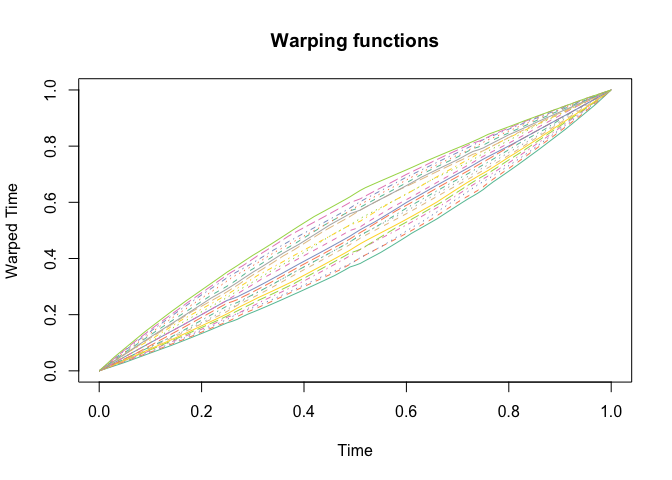
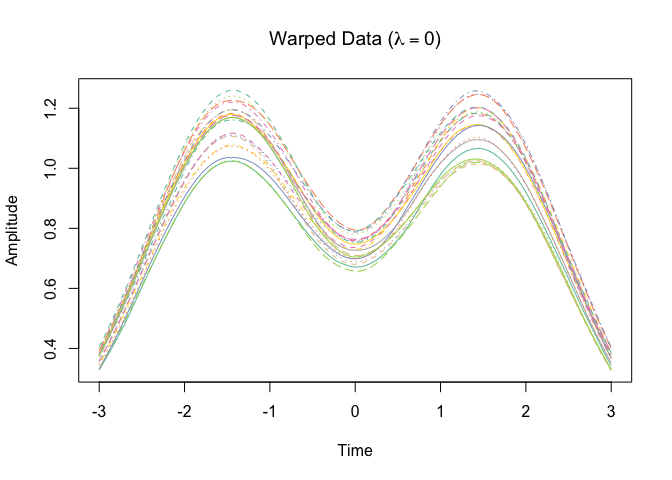
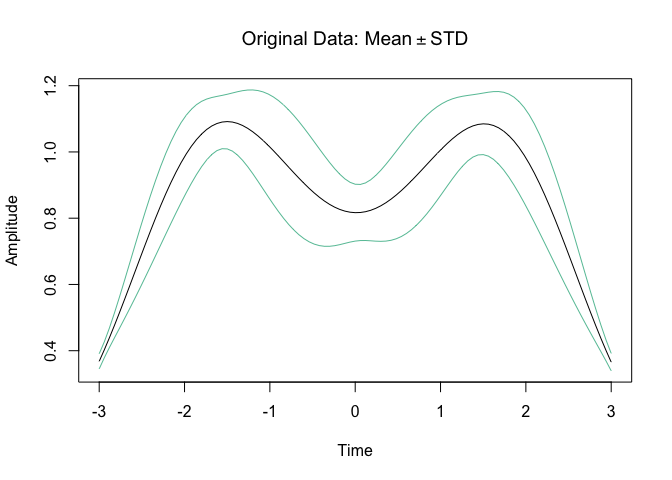
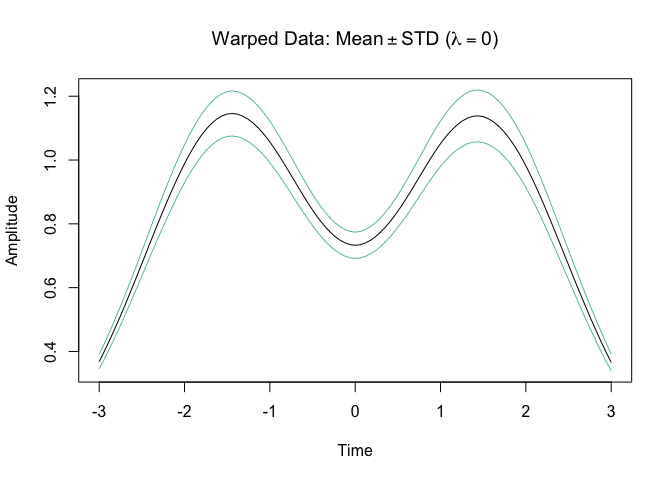
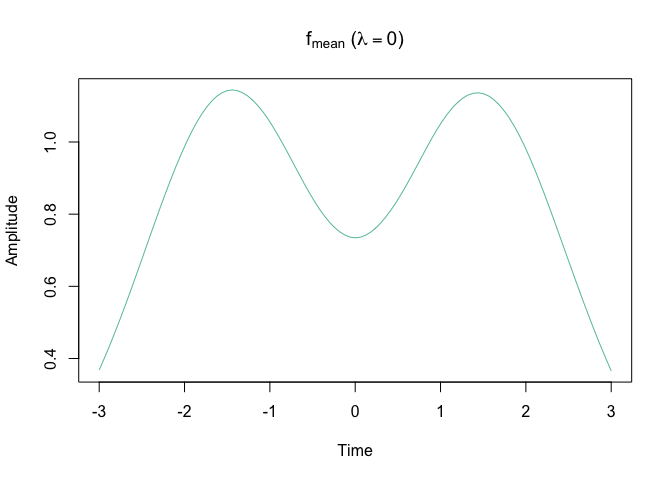
#> ℹ Entering iteration 1...Let’s plot the result
plot(obj)Tucker, J. D. 2014, Functional Component Analysis and Regression using Elastic Methods. Ph.D. Thesis, Florida State University.
Robinson, D. T. 2012, Function Data Analysis and Partial Shape Matching in the Square Root Velocity Framework. Ph.D. Thesis, Florida State University.
Huang, W. 2014, Optimization Algorithms on Riemannian Manifolds with Applications. Ph.D. Thesis, Florida State University.
Srivastava, A., Wu, W., Kurtek, S., Klassen, E. and Marron, J. S. (2011). Registration of Functional Data Using Fisher-Rao Metric. arXiv:1103.3817v2.
Tucker, J. D., Wu, W. and Srivastava, A. (2013). Generative models for functional data using phase and amplitude separation. Computational Statistics and Data Analysis 61, 50-66.
J. D. Tucker, W. Wu, and A. Srivastava, “Phase-Amplitude Separation of Proteomics Data Using Extended Fisher-Rao Metric,” Electronic Journal of Statistics, Vol 8, no. 2. pp 1724-1733, 2014.
J. D. Tucker, W. Wu, and A. Srivastava, “Analysis of signals under compositional noise With applications to SONAR data,” IEEE Journal of Oceanic Engineering, Vol 29, no. 2. pp 318-330, Apr 2014.
Srivastava, A., Klassen, E., Joshi, S., Jermyn, I., (2011). Shape analysis of elastic curves in euclidean spaces. Pattern Analysis and Machine Intelligence, IEEE Transactions on 33 (7), 1415-1428.
S. Kurtek, A. Srivastava, and W. Wu. Signal estimation under random time-warpings and nonlinear signal alignment. In Proceedings of Neural Information Processing Systems (NIPS), 2011.
Kurtek, S., Srivastava, A., Klassen, E., and Ding, Z. (2012), “Statistical Modeling of Curves Using Shapes and Related Features,” Journal of the American Statistical Association, 107, 1152–1165.
Wen Huang, Kyle A. Gallivan, Anuj Srivastava, Pierre-Antoine Absil. “Riemannian Optimization for Elastic Shape Analysis”, Short version, The 21st International Symposium on Mathematical Theory of Networks and Systems (MTNS 2014).
Cheng, W., Dryden, I. L., and Huang, X. (2016). Bayesian registration of functions and curves. Bayesian Analysis, 11(2), 447-475.
W. Xie, S. Kurtek, K. Bharath, and Y. Sun, A geometric approach to visualization of variability in functional data, Journal of American Statistical Association 112 (2017), pp. 979-993.
Lu, Y., R. Herbei, and S. Kurtek, 2017: Bayesian registration of functions with a Gaussian process prior. Journal of Computational and Graphical Statistics, 26, no. 4, 894–904.
Lee, S. and S. Jung, 2017: Combined analysis of amplitude and phase variations in functional data. arXiv:1603.01775, 1–21.
J. D. Tucker, J. R. Lewis, and A. Srivastava, “Elastic Functional Principal Component Regression,” Statistical Analysis and Data Mining, vol. 12, no. 2, pp. 101-115, 2019.
J. D. Tucker, J. R. Lewis, C. King, and S. Kurtek, “A Geometric Approach for Computing Tolerance Bounds for Elastic Functional Data,” Journal of Applied Statistics, 10.1080/02664763.2019.1645818, 2019.
T. Harris, J. D. Tucker, B. Li, and L. Shand, “Elastic depths for detecting shape anomalies in functional data,” Technometrics, 10.1080/00401706.2020.1811156, 2020.
Q. Xie, S. Kurtek, E. Klassen, G. E. Christensen and A. Srivastava. Metric-based pairwise and multiple image registration. IEEE European Conference on Computer Vision (ECCV), September, 2014
X. Zhang, S. Kurtek, O. Chkrebtii, and J. D. Tucker, “Elastic kkk-means clustering of functional data for posterior exploration, with an application to inference on acute respiratory infection dynamics”, arXiv:2011.12397 [stat.ME], 2020 arxiv
J. D. Tucker and D. Yarger, “Elastic Functional Changepoint Detection of Climate Impacts from Localized Sources”, Envirometrics, 10.1002/env.2826, 2023.