This package provides a scikit-learn-style transformer to perform OPLS. OPLS is a pre-processing method to remove variation from the descriptor variables that are orthogonal to the target variable (1).
This package also provides a class to validate OPLS models using a 1-component PLS regression with cross-validation and permutation tests (2) for both regression and classification metrics (from permutations of the target) and feature PLS loadings (from permutations of the features).
pyopls is available via pypi:
pip install pyoplsYou may also install directly from this repository for the current master:
pip install git+git://github.com/BiRG/pyopls.gitNew versions are uploaded to pypi whenever the version number is
incremented in setup.py on the master branch.
- The implementation provided here is equivalent to that of the
libPLS MATLAB library, which is a faithful
recreation of Trygg and Wold's algorithm.
- This package uses a different definition for R2X, however (see below)
OPLSinheritssklearn.base.TransformerMixin(likesklearn.decomposition.PCA) but does not inheritsklearn.base.RegressorMixinbecause it is not a regressor likesklearn.cross_decomposition.PLSRegression. You can use the output ofOPLS.transform()as an input to another regressor or classifier.- Like
sklearn.cross_decomposition.PLSRegression,OPLSwill center both X and Y before performing the algorithm. This makes centering by class in PLS-DA models unnecessary. - The
score()function ofOPLSperforms the R2X score, the ratio of the variance in the transformed X to the variance in the original X. A lower score indicates more orthogonal variance removed. OPLSonly supports 1-column targets.
A CSV file containing 1H-NMR spectra for 118 serum samples of patients
with colon cancer diagnoses and healthy controls is located in
colorectal_cancer_nmr.csv in the root of this repository (see
acknowledgment below).
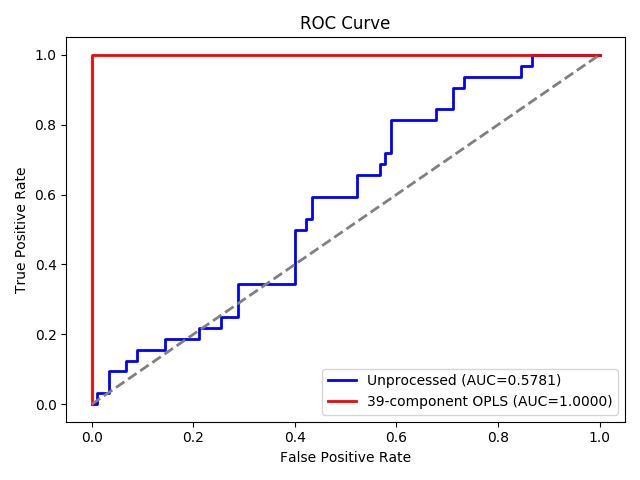
OPLS-processed data require only 1 PLS component. Performing a 39-component OPLS improves cross-validated accuracy from 70% to 100%, AUC from .578 to 1 and DQ2 (3) from 0.04 to 0.99.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, roc_auc_score
from pyopls import OPLS
from sklearn.cross_decomposition import PLSRegression
from sklearn.model_selection import cross_val_predict, LeaveOneOut
from sklearn.metrics import r2_score, accuracy_score
spectra = pd.read_csv('colorectal_cancer_nmr.csv', index_col=0)
spectra = spectra[spectra.classification.isin(['Colorectal Cancer', 'Healthy Control'])]
target = spectra.classification.apply(lambda x: 1 if x == 'Colorectal Cancer' else -1)
spectra = spectra.drop('classification', axis=1)
opls = OPLS(39)
Z = opls.fit_transform(spectra, target)
pls = PLSRegression(1)
y_pred = cross_val_predict(pls, spectra, target, cv=LeaveOneOut())
q_squared = r2_score(target, y_pred) # -0.107
dq_squared = r2_score(target, np.clip(y_pred, -1, 1)) # -0.106
accuracy = accuracy_score(target, np.sign(y_pred)) # 0.705
processed_y_pred = cross_val_predict(pls, Z, target, cv=LeaveOneOut())
processed_q_squared = r2_score(target, processed_y_pred) # 0.981
processed_dq_squared = r2_score(target, np.clip(processed_y_pred, -1, 1)) # 0.984
processed_accuracy = accuracy_score(target, np.sign(processed_y_pred)) # 1.0
r2_X = opls.score(spectra) # 7.8e-12 (most variance is removed)
fpr, tpr, thresholds = roc_curve(target, y_pred)
roc_auc = roc_auc_score(target, y_pred)
proc_fpr, proc_tpr, proc_thresholds = roc_curve(target, processed_y_pred)
proc_roc_auc = roc_auc_score(target, processed_y_pred)
plt.figure(0)
plt.plot(fpr, tpr, lw=2, color='blue', label=f'Unprocessed (AUC={roc_auc:.4f})')
plt.plot(proc_fpr, proc_tpr, lw=2, color='red',
label=f'39-component OPLS (AUC={proc_roc_auc:.4f})')
plt.plot([0, 1], [0, 1], color='gray', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc='lower right')
plt.show()
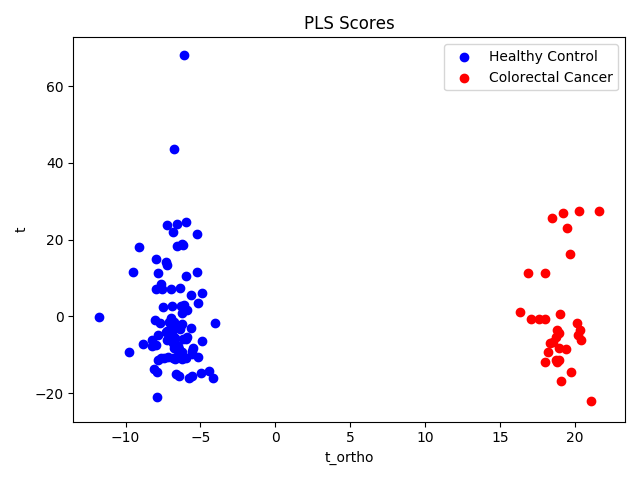
plt.figure(1)
pls.fit(Z, target)
df = pd.DataFrame(np.column_stack([pls.x_scores_, opls.T_ortho_[:, 0]]),
index=spectra.index, columns=['t', 't_ortho'])
pos_df = df[target==1]
neg_df = df[target==-1]
plt.scatter(neg_df['t'], neg_df['t_ortho'], c='blue', label='Healthy Control')
plt.scatter(pos_df['t'], pos_df['t_ortho'], c='red', label='Colorectal Cancer')
plt.title('PLS Scores')
plt.xlabel('t_ortho')
plt.ylabel('t')
plt.legend(loc='upper right')
plt.show()The fit() method of OPLSValidator will find the optimum number of
components to remove, then evaluate the results on a 1-component
sklearn.cross_decomposition.PLSRegression model. A permutation test is
performed for each metric by permuting the target and for the PLS
loadings by permuting the features.
This snippet will determine the best number of components to remove, perform permutation tests for regression metrics and perform two-tailed permutation tests for each feature (bin) relative to it's loading. The feature permutation tests for the colorectal cancer dataset would take quite some time, as they require that the model be fit as many as 874k times. So instead, we look at the UCI ML Wine Dataset provided by scikit-learn The feature permutation tests reveal that hue and malic acid do not differentate class 1 from class 0.
import pandas as pd
from pyopls import OPLSValidator
from sklearn.datasets import load_wine
wine_data = load_wine()
df = pd.DataFrame(wine_data['data'], columns=wine_data['feature_names'])
df['classification'] = wine_data['target']
df = df[df.classification.isin((0, 1))]
target = df.classification.apply(lambda x: 1 if x else -1) # discriminant for class 1 vs class 0
X = df[[c for c in df.columns if c!='classification']]
validator = OPLSValidator(k=-1).fit(X, target)
Z = validator.opls_.transform(X)
feature_df = pd.DataFrame()
feature_df['feature_name'] = wine_data['feature_names']
feature_df['feature_p_value'] = validator.feature_p_values_
feature_df['feature_loading'] = validator.pls_.x_loadings_
print(feature_df.loc[feature_df.feature_loading.abs().sort_values(ascending=False).index].to_markdown()) # Pandas 1.0+ required for to_markdown| feature_name | feature_p_value | feature_loading | |
|---|---|---|---|
| 12 | proline | 0.00990099 | 0.385955 |
| 9 | color_intensity | 0.00990099 | 0.381981 |
| 0 | alcohol | 0.00990099 | 0.379567 |
| 6 | flavanoids | 0.00990099 | 0.359975 |
| 5 | total_phenols | 0.00990099 | 0.336182 |
| 11 | od280/od315_of_diluted_wines | 0.00990099 | 0.299045 |
| 3 | alcalinity_of_ash | 0.00990099 | -0.239887 |
| 2 | ash | 0.00990099 | 0.22916 |
| 7 | nonflavanoid_phenols | 0.00990099 | -0.224338 |
| 4 | magnesium | 0.00990099 | 0.18662 |
| 8 | proanthocyanins | 0.00990099 | 0.181767 |
| 1 | malic_acid | 0.564356 | 0.0293328 |
| 10 | hue | 0.623762 | 0.0210777 |
- Johan Trygg and Svante Wold. Orthogonal projections to latent structures (O-PLS). J. Chemometrics 2002; 16: 119-128. DOI: 10.1002/cem.695
- Eugene Edington and Patrick Onghena. "Calculating P-Values" in Randomization tests, 4th edition. New York: Chapman & Hall/CRC, 2007, pp. 33-53. DOI: 10.1201/9781420011814.
- Johan A. Westerhuis, Ewoud J. J. van Velzen, Huub C. J. Hoefsloot, Age K. Smilde. Discriminant Q-squared for improved discrimination in PLSDA models. Metabolomics 2008; 4: 293-296. DOI: 10.1007/s11306-008-0126-2
The test dataset provided at pyopls/tests/colorectal_cancer_nmr.csv is
available at the NIH Common Fund's National Metabolomics Data Repository
(NMDR) website, the Metabolomics Workbench,
[https://metabolomicsworkbench.org] where it has been assigned Project
ID PR000227. The data can be accessed directly via it's Project DOI
10.21228/M89P43. This work is
supported by NIH grant, U2C-DK119886.
Note: The test dataset consists only of those spectra belonging to samples labeled "Colorectal Cancer" or "Healthy Control". The "target" variable has the value -1 for samples labeled "Healthy Control" and value +1 for samples labeled "Colorectal Cancer".