bayesNMF: an R package for Bayesian NMF

Notes

Hello! This package is a work in progress and new features will be added periodically.

The following likelihood - prior combinations have been implemented:

Poisson - Gamma: $M \sim Poisson(PE)$, $P$ and $E$ follow Gamma priors
Poisson - Exponential: $M \sim Poisson(PE)$, $P$ and $E$ follow Exponential priors
Normal - Truncated Normal: $M_k \sim N((PE)_k, \sigma^2_k I)$, $P$ and $E$ follow Truncated-Normal priors, $\sigma^2_k$ follows an Inverse-Gamma prior
Normal - Exponential: $M_k \sim N((PE)_k, \sigma^2_k I)$, $P$ and $E$ follow Exponential priors, $\sigma^2_k$ follows an Inverse-Gamma prior

While language and simulation examples are in the context of mutational signatures analysis, this package can be used for any application of NMF.

Quick Start

Installation

library(devtools)
devtools::install_github("jennalandy/bayesNMF")
library(bayesNMF)

Use

The main function is bayesNMF, which runs a Gibbs sampler and reports the MAP estimates.

As with standard NMF, bayesNMF requires the latent rank N be provided.

rank5_results <- bayesNMF(
    M, N = 5, 
    likelihood = "normal", 
    prior = "truncnormal", 
    file = "my_run_rank5"
)

Three files will be created and updated every 100 iterations by default (can be controlled with the logevery parameter)

my_run_rank5.log will log the start time and the progress of the Gibbs sampler, which is useful to estimate the total run time if using a large dataset or a lot of iterations.
my_run_rank5.rds records the current results, which is be useful if your run is cut short (the dreaded OOM error). Once the function is complete, this records complete results for future access.
my_run_rank5.pdf updates plots of metrics: RMSE, KL Divergence, BIC, log posterior, log likelihood, and latent rank of periodically computed MAP estimates (see the section on convergence below for details). Note that for log likelihood and log posterior, values from the Poisson models are not comparable to those from Normal models.

The maximum a-posteriori (MAP) estimates for $P$ and $E$ are stored in rank5_results$MAP$P and rank5_results$MAP$E. The full Gibbs sampler chains are stored in rank5_results$logs if store_logs = TRUE (default). The periodic metrics of MAP estimates displayed in my_run_rank5.pdf are stored in rank5_results$metrics.

Iterations to Convergence

Unlike standard MCMC problems, we cannot use multiple chains to determine convergence because different chains can have different numbers of latent factors which we would be unable to align. We instead determine convergence through an approach rooted in machine learning. The convergence_control parameter determines the specifics of this approach. These parameters can be adjusted by the user, but the default values are noted below.

new_convergence_control = convergence_control(
    MAP_over = 1000,
    MAP_every = 100,
    tol = 0.001,
    Ninarow_nochange = 10,
    Ninarow_nobest = 20,
    miniters = 1000,
    maxiters = 10000,
    metric = "loglikelihood"
)

We pre-determine that the MAP estimate will be the average over MAP_over samples. Starting at miniters and at every MAP_every samples after, we compute the MAP estimate as if it is the last iteration and record log likelihood, log posterior, RMSE, and KL Divergence. We say the MAP "hasn't changed" if it's log likelihood has changed by less than 100*tol% since the previous computed MAP. We say the MCMC has converged when the MAP hasn't changed in Ninarow_nochange computations (i.e., Ninarow_nochange*MAP_every samples) OR if it hasn't improved in Ninarow_nobest computations (i.e., Ninarow_nobest*MAP_every samples).

Learning Rank

We have also implemented an option to learn the rank as a part of the Bayesian model when max_N is provided instead of N. Note that this takes many more samples to converge than the model with a fixed N. We are still working to find the best number of samples for convergence. Right now, we (by default) run models with Normal likelihoods for 5000 samples (3500 for burn-in) and Poisson likelihoods for 10000 samples (7500 for burn-in).

learned_rank_results <- bayesNMF(
    M, max_N = 7, 
    likelihood = "normal", 
    prior = "truncnormal", 
    file = "my_run_learned_rank"
)

Here, an additional matrix $A$ is estimated, which determines which latent factors are included in the final model. learned_rank_results$MAP$A is dimension 1 by max_N. For each position $n$, a 1 indicates factor $n$ is included, while a 0 indicates the factor was dropped. Dropped factors have already been removed from learned_rank_results$MAP$P and learned_rank_results$MAP$E.

When learning rank, the model employs hyperprior distributions so that prior parameters are updated at each iteration.

Compare to True or Literature Signatures

We also include commands to compare estimated signatures to the true signatures matrix to evaluate simulation studies. This could also be a set of signatures from literature that we wish to use as a baseline.

The following functions provide a similarity matrix between the true and estimated $P$ matrices, as well as a heatmap to visualize this.

sim_mat <- pairwise_sim(res$MAP$P, true_P)
heatmap <- get_heatmap(est_P = res$MAP$P, true_P = true_P)

You can also do this all in one call. If true_P is provided to bayesNMF, then the similarity matrix and heatmap are stored in res$sim_mat and res$heatmap, respectively.

rank5_results <- bayesNMF(
    M, N = 5, 
    likelihood = "normal", 
    prior = "truncnormal", 
    file = "my_run_rank5",
    true_P = true_P
)

Recovery-Discovery Option

If recovery = TRUE and recovery_priors are provided, then the model will use a combination of these priors an N or max_N standard priors. This is particularly useful in the context of mutational signatures, where we may want our recovery priors to match the reference signatures in the COSMIC database. For Normal likelihood models, recovery_priors = "cosmic" (default) can be used as a shortcut. Alternatively, a P matrix can be provided to the get_recovery_priors function to generate recovery priors that can then be provided to bayesNMF.

This example uses recovery priors for the 79 COSMIC signatures. This means we are learning between 0 and 49 + 7 = 56 latent factors, where 49 have priors set at the COSMIC recovery priors, and the other 7 have priors with the standard hyperprior distributions that are updated at each iteration.

learned_rank_recovery_discover_results <- bayesNMF(
    M, max_N = 7, 
    likelihood = "normal", 
    prior = "truncnormal", 
    file = "my_run_learned_rank",
    recovery = TRUE,
    recovery_priors = "cosmic"
)

This is an example with a user-provided P matrix, literature_P, perhaps containing latent factors discovered in a previous analysis.

recovery_priors = get_recovery_priors(literature_P)
learned_rank__recovery_discover_results <- bayesNMF(
    M, max_N = 7, 
    likelihood = "normal", 
    prior = "truncnormal", 
    file = "my_run_learned_rank",
    recovery = TRUE,
    recovery_priors = recovery_priors
)


## Simulated Example

### 1. Simulate Data

Here we simulate a mutational catalog based on a subset of COSMIC signatures, available at the link below. We use 5 of the COSMIC signatures as the true P matrix.

```{r}
set.seed(123)

sigs = c(2,3,4,5,6)
N = length(sigs)
P <- read.csv(
  "https://cog.sanger.ac.uk/cosmic-signatures-production/documents/COSMIC_v3.3.1_SBS_GRCh37.txt",
  sep = '\t'
)
P <- as.matrix(P[,sigs])
K = nrow(P)

We then simulate exposure values, for example here from an exponential distribution. We generate exposures for G = 20 samples.

G = 20
E <- matrix(rexp(N*G, 0.001), nrow = N, ncol = G)

Assuming a Poisson data generating function, we can finally simulate a mutational catalog $M$.

M <- matrix(nrow = K, ncol = G)
for (k in 1:K) {
    M[k,] <- rpois(G, P[k,]%*%E)
}

Below shows the six number summary for the number of mutations per sample. We see that the central 50% of generated samples have between 2963 and 5231 mutations.

summary(colSums(M))

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1699    2963    4891    5231    7410    9845

2. Running Methods

Now we can run the Normal-Exponential model of Bayesain NMF.

res <- bayesNMF(
  M, N = 5,
  likelihood = "normal",
  prior = "truncnormal",
  file = "my_run",
  true_P = P
)

3. Evaluating Methods

Metrics are always recorded on each iteration. Here we look at the metrics on the last iteration.

data.frame(res$metrics)[res$niters,]

         loglik     RMSE       KL
1500 -191938493 5.679985 792.8074

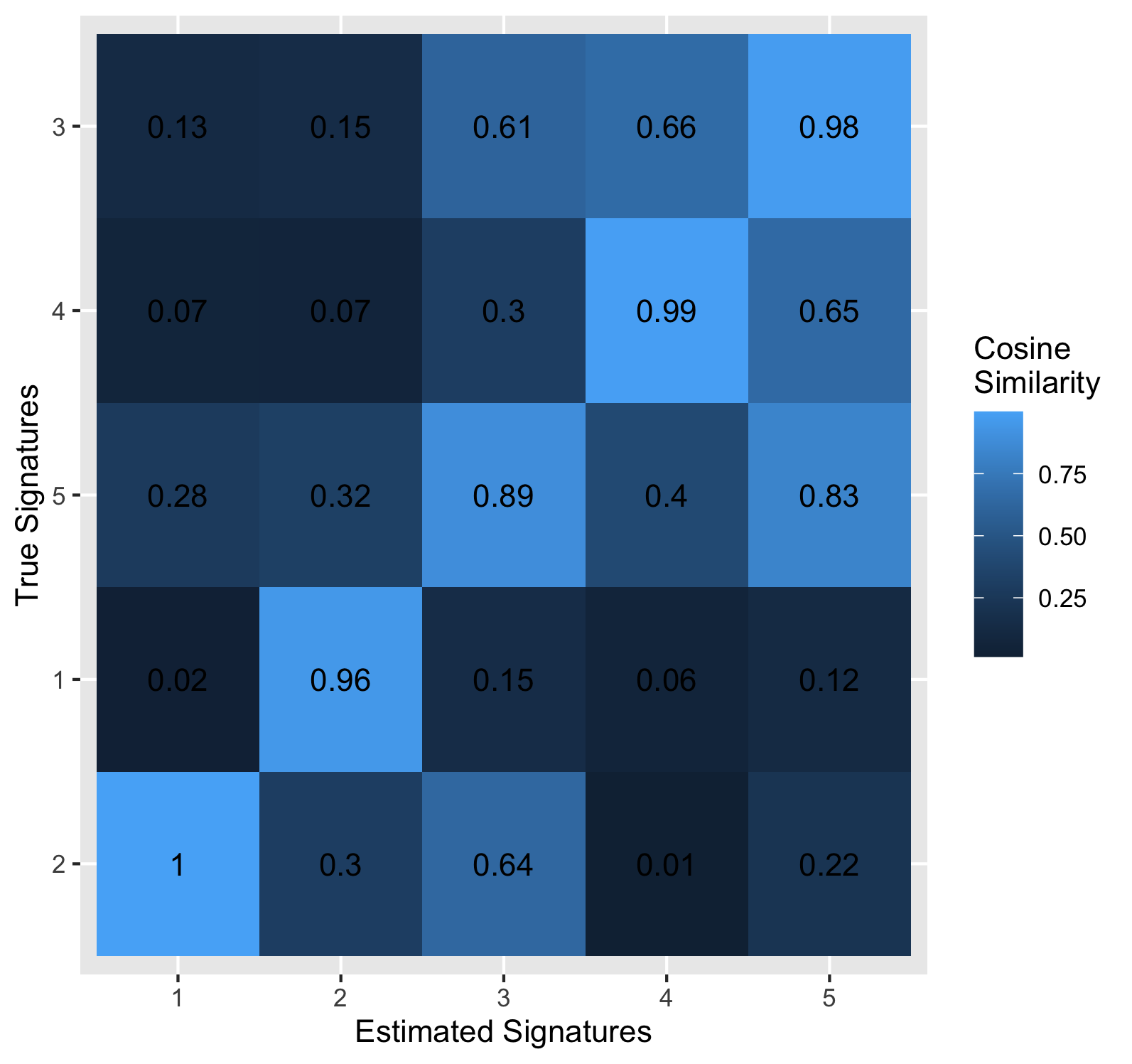
The similarity matrix and corresponding heatmap are only provided if true_P is used.

res$sim_mat

                true1      true2     true3      true4     true5
estimated1 0.02424170 0.99924989 0.1298875 0.06788912 0.2774230
estimated2 0.95511900 0.30313309 0.1460383 0.06711596 0.3237289
estimated3 0.14618485 0.63629489 0.6070845 0.30329985 0.8874797
estimated4 0.06009177 0.01311398 0.6603101 0.99498287 0.4026305
estimated5 0.12359146 0.21950484 0.9810274 0.64979449 0.8274775

res$heatmap

Notice that signatures are reordered on the heatmap, assigned using the Hungarian algorithm. To see this assignment on the similarity matrix, you can use the assign_signatures function. Here, we can see that our estimated factor 1 was assigned matches best to the true factor 2.

assigned_sim_mat = assign_signatures(res$sim_mat)
assigned_sim_mat

                true2      true1     true5      true4     true3
estimated1 0.99924989 0.02424170 0.2774230 0.06788912 0.1298875
estimated2 0.30313309 0.95511900 0.3237289 0.06711596 0.1460383
estimated3 0.63629489 0.14618485 0.8874797 0.30329985 0.6070845
estimated4 0.01311398 0.06009177 0.4026305 0.99498287 0.6603101
estimated5 0.21950484 0.12359146 0.8274775 0.64979449 0.9810274