jessaskey/Computational-geometry

Computational Geometry Unity library with implementations of intersection algorithms, triangulations like delaunay, voronoi diagrams, polygon clipping, bezier curves, etc

Computational Geometry Unity Library

This library consists of two folders. The idea is that one is for testing purposes and the other folder is the folder you drag into your project.

Make sure all input coordinates are normalized to range 0-1 to avoid floating point precision issues! Normalizing methods exists in HelpMethods. This is not always needed but if you notice that an algorithm doesn't work, try to normalize the input coordinates.

Some of these algorithms are available in tutorial form here: https://www.habrador.com/tutorials/math/ and here: https://www.habrador.com/tutorials/interpolation/

The code has been tested by using Unity 2018.4 LTS but should work with other versions.

Finished

1. Intersection

1.1 2d-space

Point-triangle

Point-polygon. Suffers from floating point precision issues

Triangle-triangle

AABB-AABB

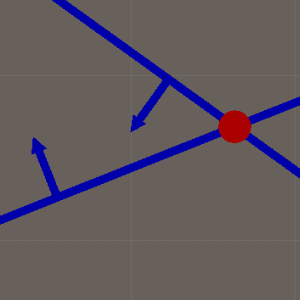
Line-line

Ray-plane

Line-plane

Plane-plane

Point-circle

2. Generate mesh

Grid mesh

Mesh shapes: Arrow, circles, lines

3. Convex Hull

A common problem in Computational Geometry is to find the convex hull of a set of points.

Jarvis March. Is also known as "Gift wrapping"

This is the simplest algorithm. The idea is:

1. Find a point on the hull (which can be the point with the smallest x-coordinate)
2. To find the next point on the hull, you pick a point randomly, and then you test all other points if the other point is to the right of the point between the last point on the hull and the point you picked randomly. If so then this point is a better point. You continue like this until you find no more point to the right. This last point is also on the hull.

This algorithm may be slow, but it is robust and can easily deal with colinear points. Sometimes it's better to use an algorithm which is easy to understand than a more complicated one.

A visualization of this algorithm can be found here: https://www.youtube.com/watch?v=Z_wcJUgvohc

Quickhull.

A good paper on this algorithm is "Implementing Quickhull" from Valve by Dirk Gregorious. It has images so you can see what's going on. But the idea is:

1. Find a first triangle with three points that are on the hull. Now you can remove all points that are within this triangle
2. For each edge (you start with the triangle's three edges) find the points that are "outside" of this edge
3. For each edge (and by using the points you know are outside of this edge) find the point that is the furthest from this edge. This point is also on the hull. Now the original edge on the triangle has been split into two. Remove all points that are within this new triangle formed by the original edge and the two new edges.
4. Repeat 2 and 3 for each new edge

4. Triangulation

Triangulate convex polygon.

You have points on a convex hull you want to triangulate. You have four options here if you have colinear points (points on the same line):

1. Triangulate the convex hull while ignoring the colinear points. The area covered will be the same anyway.
2. Triangulate the convex hull and add the colinear points by splitting triangle edges.
3. Add a point inside of the convex hull.
4. Use the algorithm below called "Triangulate points with 'visible edge' algorithm."

Triangulate points with "visible edge" algorithm.

You have some points you want to triangulate, you follow the steps:

1. Sort all points in x and then y direction
2. Find the first triangle
3. Add the rest of the sorted points one-by-one and build triangles to visible edges on the existing triangulation. To determine if an edge is visible from the point you build the convex shape from the existing triangles. Then for each edge in the convex hull, you build a triangle with the point. If this triangle is oriented clockwise, the edge is visible and you can add a new triangle.

A visualization of this algorithm can be found here: https://www.youtube.com/watch?v=MkMXKu1m6A4

Triangulate points with "point-by-point" algorithm.

You have some points you want to triangulate, you follow the steps:

1. Generate the convex hull of all points.
2. Triangulate the convex hull with one of several algorithms mentioned above.
3. Add the rest of the points one-by-one by splitting the triangles they end up in into three new triangles.

4.1 Delaunay triangulation

"point-by-point" method

You generate a big triangle around all points you want to triangulate. Then you add each point one after the other. The triangle the point ends up in is split into three new triangles. After the split you restore the Delaunay triangulation by flipping edges. When all points have been added you remove the remains of the first big triangle. A visualization of this algorithm can be found here: https://www.youtube.com/watch?v=YNQR5tH-s40

"flip edges" method

You triangulate the points by using a "bad" triangulation method (which is in this case either "visible edge" or "point-by-point" from above). Then you go through all edges and check if the edge should be flipped to make a better triangle. When no more edges can be flipped you are done! A visualization of this algorithm can be found: https://www.youtube.com/watch?v=-d7Nb4fxL5s and https://www.youtube.com/watch?v=lR_SzgEkDwk

Constrained triangulation

You add the constraints to the points and generate a Delaunay triangulation by using one of the above methods. Use this triangulation to find which edges interesect with the constraints. Then you flip these edges until they no longer interesect with the constraint. You finally remove the triangles that are "inside" of the constraint. It can currently handle just one hole, but in theory it can handle as many holes as possible, so I will add that in the future.

5. Voronoi diagram

From a Delaunay triangulation

You first generate a Delaunay triangulation by using some method. Then you use the fact that you can get the Voronoi diagram from the Delaunay triangulation. For each Delaunay triangle you generate a circle where the triangle-corners are on the edge of the circle. The center of this circle is a corner in the Voronoi diagram face belonging to the triangle.

6. Polygon clipping

Greiner-Hormann method

Sutherland-Hodgman method

7. Interpolation

Catmull-Rom splines

Bezier curves

• Linear

• Quadratic

• Cubic

There's also methods so you can split up the curves into equal steps.

8. Other

Is a triangle oriented clockwise?

Is a point left, on, or right of vector?

Is a point left, on, or right of a plane? Which is the same as the distance to the plane.

Is a quadrilateral convex?

Is a point between two other points on the same line?

Closest point on a line-segment?

Has passed point?

If we are going from A to B, how do we know if we have passed B? Measuring just the distance to B, and say we have passed B if we are closer than x meter to B is not accurate enough!

TODO

Algorithms to implement

• Dynamic constrained delaunay triangulation
• Convex hull: Graham scan
• Triangulate with Marching cubes
• Cut 3d mesh with plane
• Metaballs
• Voronoi with Fortune's algorithm
• Voronoi point-by-point
• Triangulation concave polygon by ear clipping (You can most likely achieve the same thing with Constrained Delaunay, so maybe unnecessary to implement)
• Convex polygon intersection with SAT
• Triangulate with marching squares
• Irregular grid (Oskar Stålberg style)

Stuff to fix

• Optimize Constrained Delaunay - there's a faster method to find edges that intersects with the constrained edge. I also think the method where triangles within the constrain is removed can be faster.
• Make a test scene to test that the "find which triangle a point is in by triangulation walk" is working
• The Delaunay algorithm "flip edges" might have problems with colinear points

Socials

• Portfolio: https://www.habrador.com

• Twitter: https://twitter.com/eriknordeus

Updates

2020-03

• Added interpolation such as Bezier curves and Catmull-Rom