jgabry/mcmc-demo

Interactive Markov-chain Monte Carlo Javascript demos

The Markov-chain Monte Carlo Interactive Gallery

Example: Hamiltonian Monte Carlo

Click on an algorithm below to view an interactive demo where you can change algorithm parameters on-the-fly:

Standard MCMC methods

• Random Walk Metropolis Hastings
• Adaptive Metropolis Hastings [1]
• Hamiltonian Monte Carlo [2]
• No-U-Turn Sampler [2]
• Metropolis-adjusted Langevin Algorithm (MALA) [3]
• Hessian-Hamiltonian Monte Carlo (H2MC) [4]
• Gibbs Sampling
• DE-MCMC-Z [7]

Non-Markovian iterative sampling methods

• Stein Variational Gradient Descent (SVGD) [5]
• Nested Sampling with RadFriends (RadFriends-NS) [6]

References

[1] H. Haario, E. Saksman, and J. Tamminen, An adaptive Metropolis algorithm (2001)

[2] M. D. Hoffman, A. Gelman, The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo (2011)

[3] G. O. Roberts, R. L. Tweedie, Exponential Convergence of Langevin Distributions and Their Discrete Approximations (1996)

[4] Li, Tzu-Mao, et al. Anisotropic Gaussian mutations for metropolis light transport through Hessian-Hamiltonian dynamics ACM Transactions on Graphics 34.6 (2015): 209.

[5] Q. Liu, et al. Stein Variational Gradient Descent: A General Purpose Bayesian Inference Algorithm Advances in Neural Information Processing Systems. 2016.

[6] J. Buchner A statistical test for Nested Sampling algorithms Statistics and Computing. 2014.

[7] Cajo J. F. ter Braak & Jasper A. Vrugt Differential Evolution Markov Chain with snooker updater and fewer chains Statistics and Computing. 2008.

Running locally

Clone or download the repository and open index.html in your web browser. All dependencies are included in in lib/.

Adding an algorithm

1. Copy one of the existing algorithms in the algorithms directory (a good starting point is algorithms/HamiltonianMC.js).
2. in app.html include the your algorithm's javascript file at the bottom of the page. This will add your algorithm to the dropdown menu.
3. Add any new visualizations to the Visualizer.prototype.dequeue function defined in main/Visualizer.js. The MCMC simulation adds visualization "events" onto an animation queue. Most common events such as accepting or rejecting a proposal have already been implemented. The renderer composites the contents of three offscreen canvases (densityCanvas, samplesCanvas, and overlayCanvas)
4. Add a link to your algorithm in README.md and index.html

See also

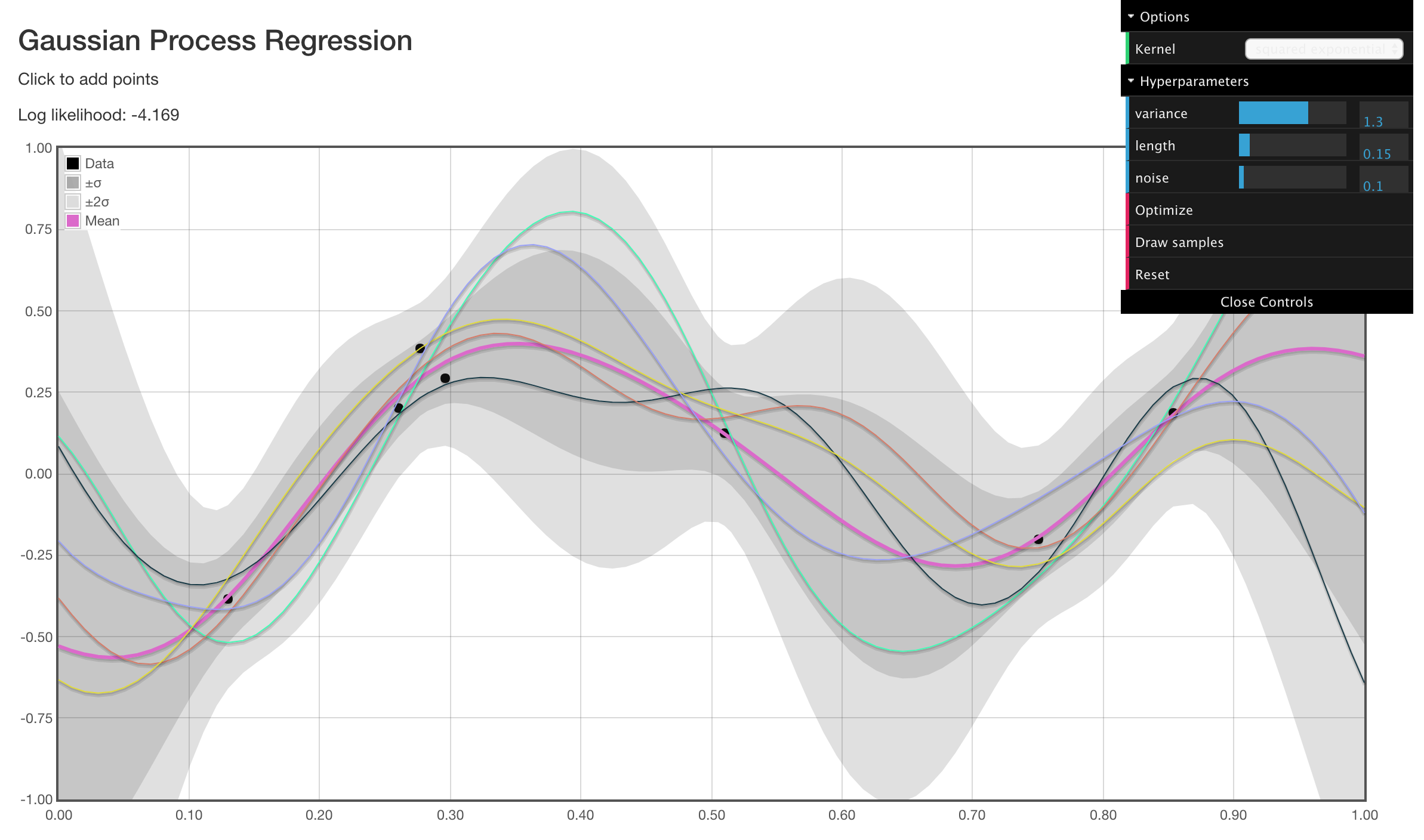
Interactive Gaussian process regression demo

https://github.com/chi-feng/gp-demo