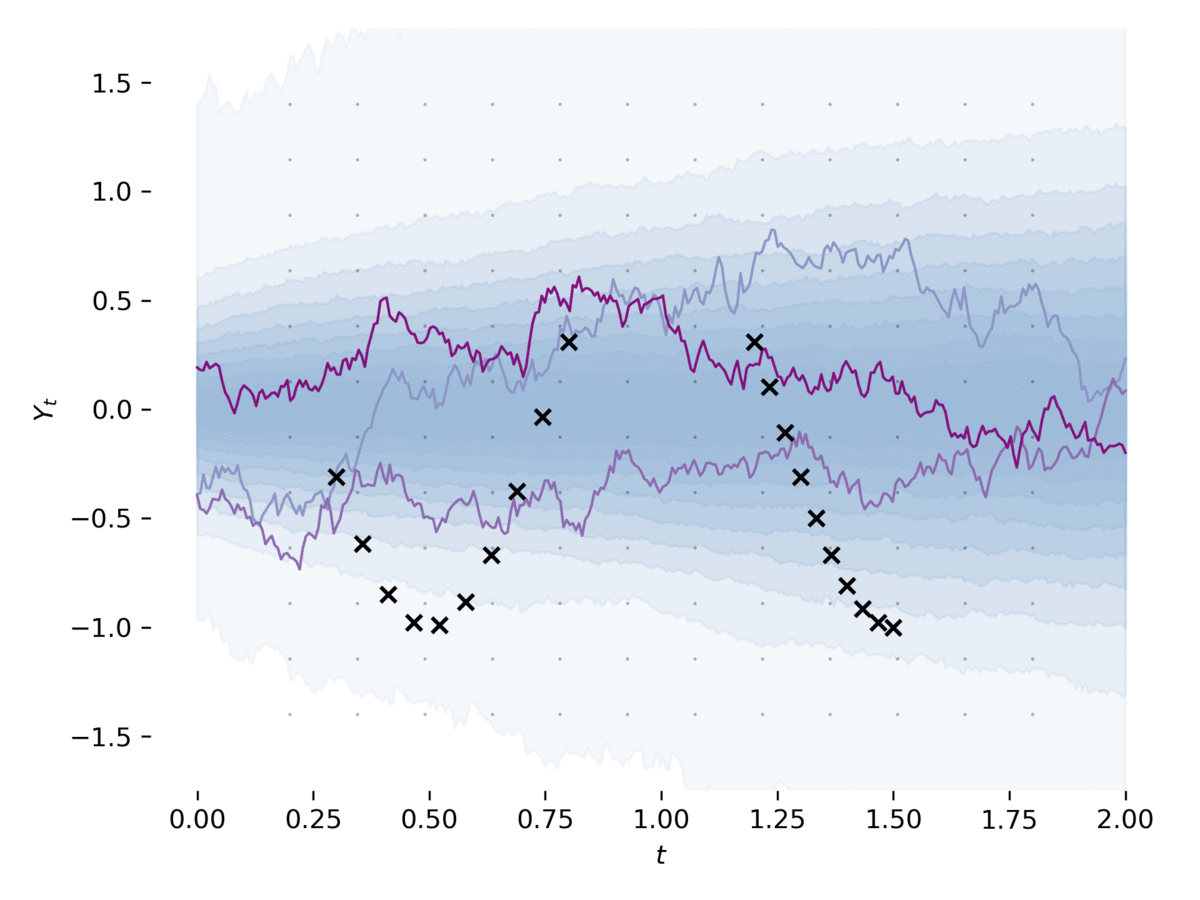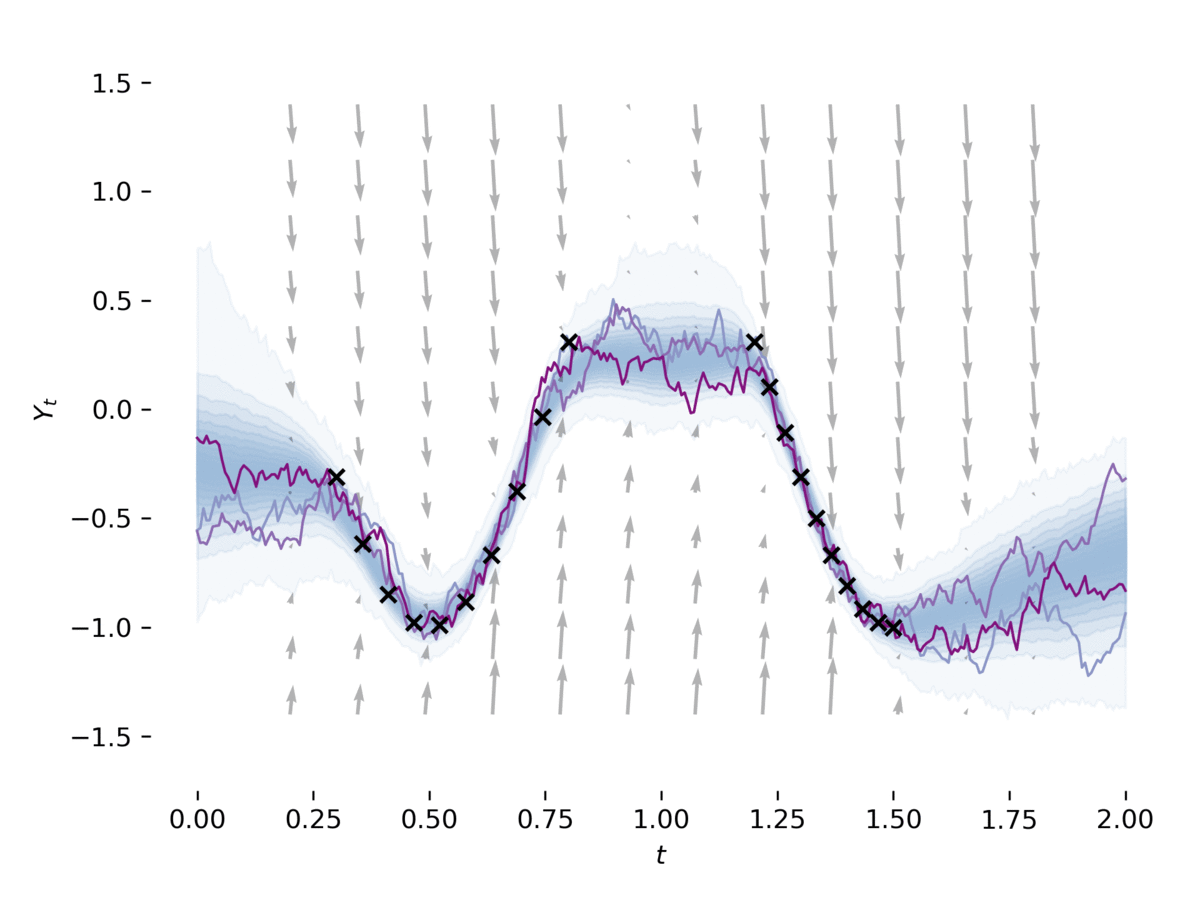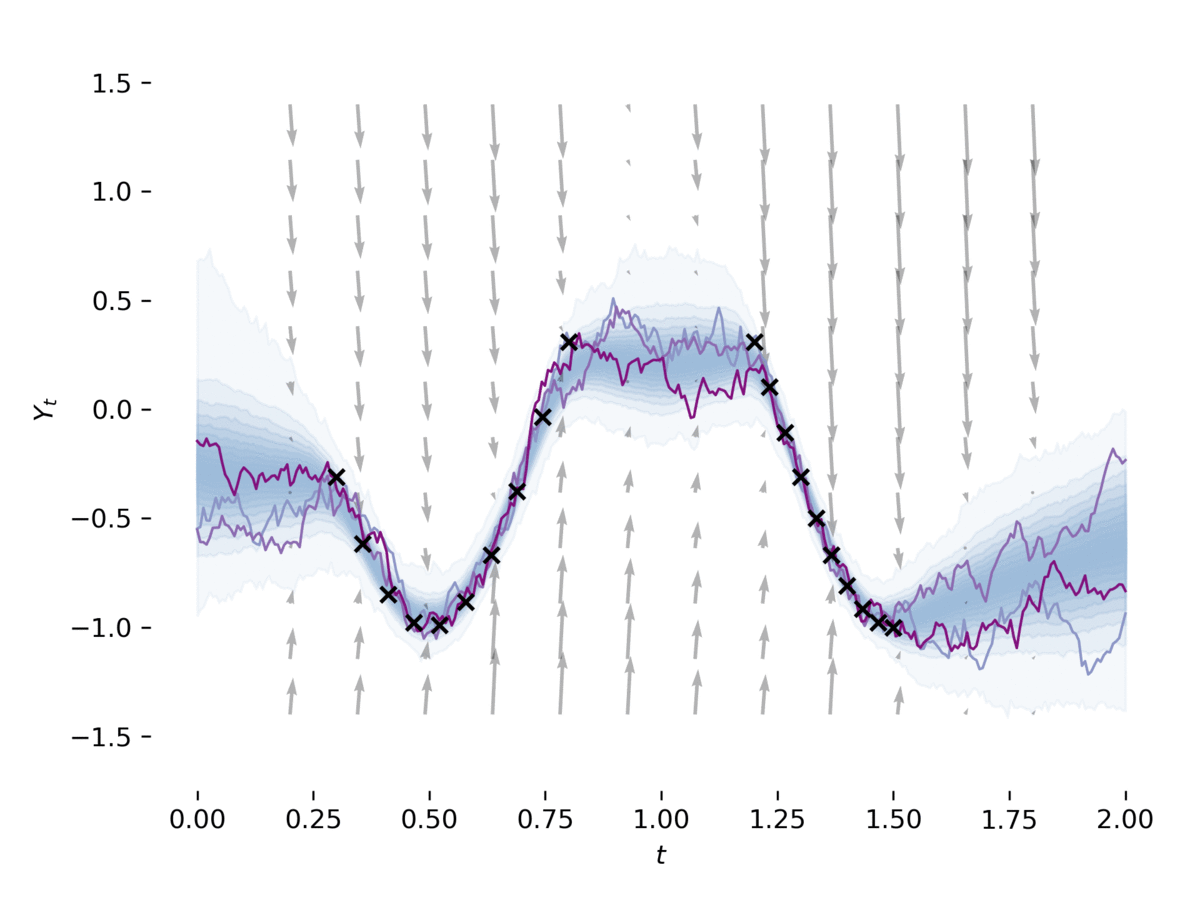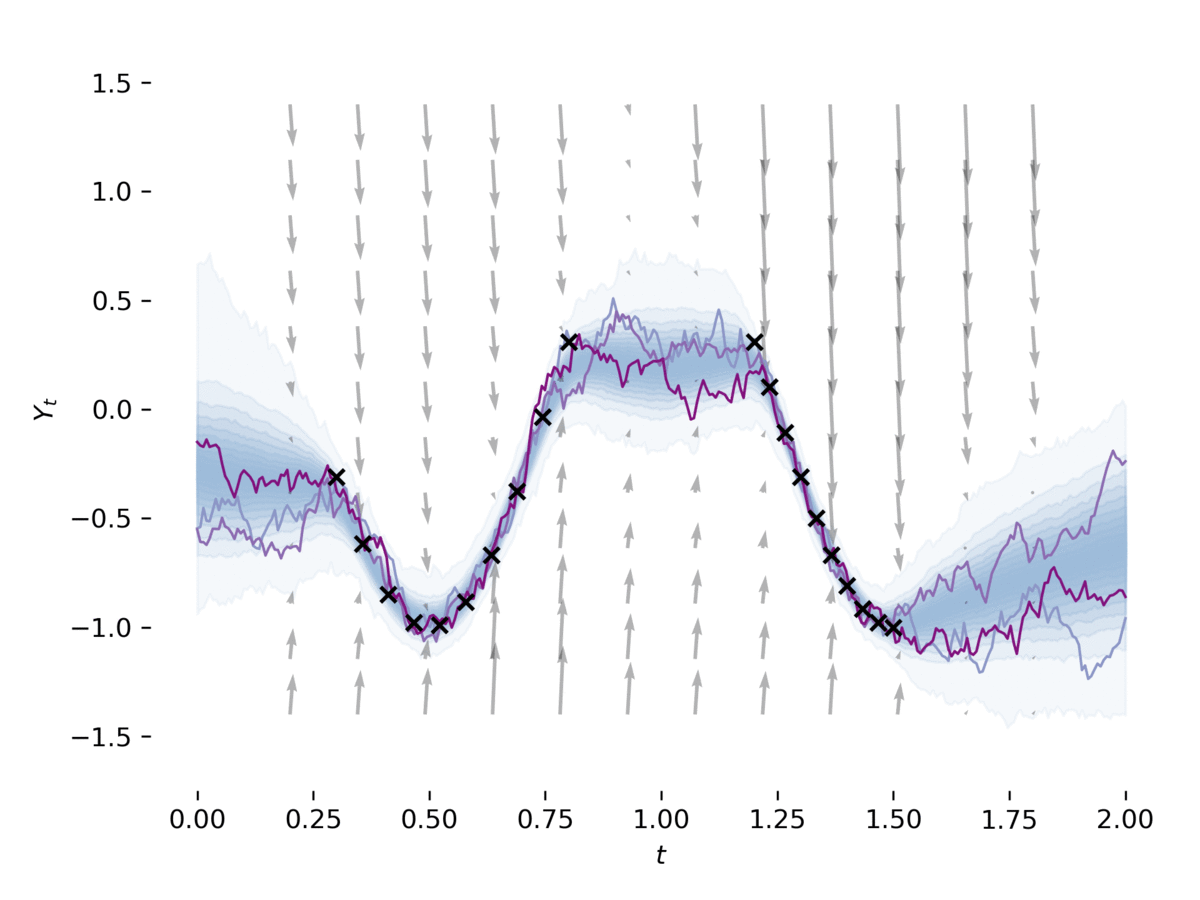
PyTorch Implementation of Differentiable SDE Solvers

This library provides stochastic differential equation (SDE) solvers with GPU support and efficient backpropagation.

Installation

pip install torchsde

Requirements: Python >=3.6 and PyTorch >=1.6.0.

Documentation

Available here.

Examples

Quick example

import torch
import torchsde

batch_size, state_size, brownian_size = 32, 3, 2
t_size = 20

class SDE(torch.nn.Module):
    noise_type = 'general'
    sde_type = 'ito'

    def __init__(self):
        super().__init__()
        self.mu = torch.nn.Linear(state_size, 
                                  state_size)
        self.sigma = torch.nn.Linear(state_size, 
                                     state_size * brownian_size)

    # Drift
    def f(self, t, y):
        return self.mu(y)  # shape (batch_size, state_size)

    # Diffusion
    def g(self, t, y):
        return self.sigma(y).view(batch_size, 
                                  state_size, 
                                  brownian_size)

sde = SDE()
y0 = torch.full((batch_size, state_size), 0.1)
ts = torch.linspace(0, 1, t_size)
# Initial state y0, the SDE is solved over the interval [ts[0], ts[-1]].
# ys will have shape (t_size, batch_size, state_size)
ys = torchsde.sdeint(sde, y0, ts)

Notebook

examples/demo.ipynb gives a short guide on how to solve SDEs, including subtle points such as fixing the randomness in the solver and the choice of noise types.

Latent SDE

examples/latent_sde.py learns a latent stochastic differential equation, as in Section 5 of [1]. The example fits an SDE to data, whilst regularizing it to be like an Ornstein-Uhlenbeck prior process. The model can be loosely viewed as a variational autoencoder with its prior and approximate posterior being SDEs. This example can be run via

python -m examples.latent_sde --train-dir <TRAIN_DIR>

The program outputs figures to the path specified by <TRAIN_DIR>. Training should stabilize after 500 iterations with the default hyperparameters.

Neural SDEs as GANs

examples/sde_gan.py learns an SDE as a GAN, as in [2], [3]. The example trains an SDE as the generator of a GAN, whilst using a neural CDE [4] as the discriminator. This example can be run via

python -m examples.sde_gan

Citation

If you found this codebase useful in your research, please consider citing either or both of:

@article{li2020scalable,
  title={Scalable gradients for stochastic differential equations},
  author={Li, Xuechen and Wong, Ting-Kam Leonard and Chen, Ricky T. Q. and Duvenaud, David},
  journal={International Conference on Artificial Intelligence and Statistics},
  year={2020}
}

@article{kidger2021neuralsde,
  title={Neural {SDE}s as {I}nfinite-{D}imensional {GAN}s},
  author={Kidger, Patrick and Foster, James and Li, Xuechen and Oberhauser, Harald and Lyons, Terry},
  journal={International Conference on Machine Learning},
  year={2021}
}

References

[1] Xuechen Li, Ting-Kam Leonard Wong, Ricky T. Q. Chen, David Duvenaud. "Scalable Gradients for Stochastic Differential Equations". International Conference on Artificial Intelligence and Statistics. 2020. [arXiv]

[2] Patrick Kidger, James Foster, Xuechen Li, Harald Oberhauser, Terry Lyons. "Neural SDEs as Infinite-Dimensional GANs". International Conference on Machine Learning 2021. [arXiv]

[3] Patrick Kidger, James Foster, Xuechen Li, Terry Lyons. "Efficient and Accurate Gradients for Neural SDEs". 2021. [arXiv]

[4] Patrick Kidger, James Morrill, James Foster, Terry Lyons, "Neural Controlled Differential Equations for Irregular Time Series". Neural Information Processing Systems 2020. [arXiv]

This is a research project, not an official Google product.

jiangsy/torchsde