My EasyGL (Let's play with Geometry)

This repo contains my own adaptions for 3 geometry processing libraries:

ACAM https://github.com/USTC-GCL-F/AMMesh
CGAL-5.3
Libigl

Video Link

https://www.bilibili.com/video/BV1B54y1B7Uc

Design Principles and Code Style

Libigl
Basic type such as vec, matrix must follow Eigen's API
for template class, implementation is in the header file
for short member function, implementation is in the header file
const global varaible: const INVALID_IND = ...;
class's member variable: mClsMemVar, or, memVar_, to distiguish from local variables

ToDO:

How to find the light direction given an image: n.dot(light) = diffuse Can I add normal info when doing laplace inflation? Read Interactive Normal Paper

implement direct laplace smooth and implicit laplace smooth

CGAL

Euler Operation

Euler::collapse_edge(e, g)

Curvature

Mean Curvature H = K1 + K2: extrinsic

Mean Curvature Normal: L*X = -2 * H * normal

Gaussian Curvature K = K1 * K2: 2 * PI - one_ring_triangle_incident_angle: intrinsic

K > 0: elliptical local convexity, sum_OneRignIncidentAngles < 2 * PI, a elliptical point
K = 0: hyperbolic, sum_OneRignIncidentAngles == 2 * PI, a flat plane
K < 0: parabolic saddle points, sum_OneRignIncidentAngles > 2 * PI, a saddle point

Skeleton Extraction by Mesh Contraction

Derive shape cost K by hand

Implicit Laplace Smoothing

Let the vertex flow into mean-curvature normal.

du / dt = L * u
u(t+1) - u(t) = L * u(t+1)

so, solve (I-L)* u(t+1) = u(t)

Implementation

// M: mass matrix, Lcot: cotmatrix, L: laplace matrix, L = Minv * Lcot
// (I-L) * u(t+1) = u(t)
// (I-Minv*Lcot) * u(t+1) = u(t)
// (M - Lcot) * u(t+1) = u(t)
// so solve: (M - Lcot) * u(t+1) = u(t)

How to dervie point-to-edge distance Matrix Kij?

ToDO: validate in code

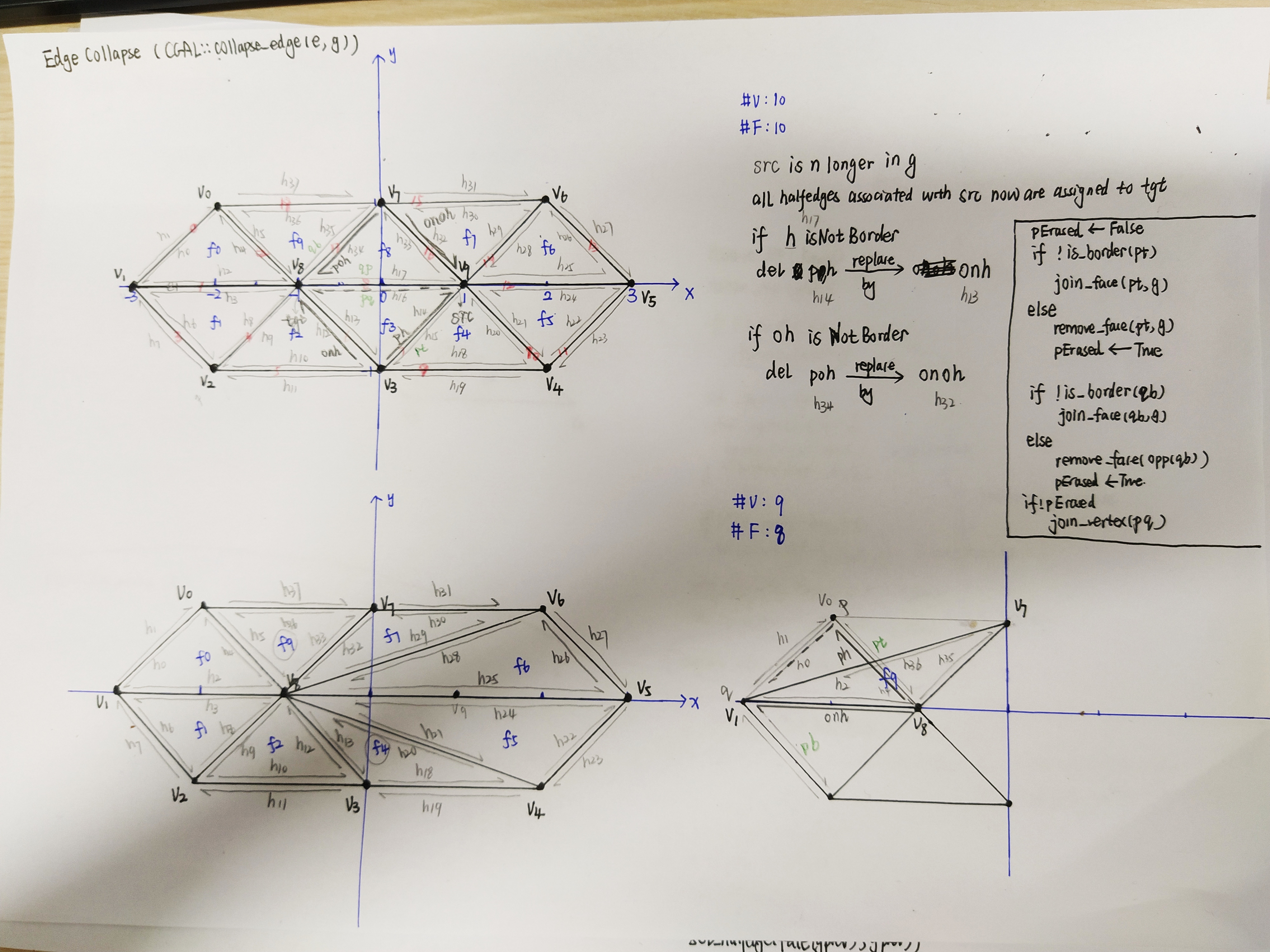
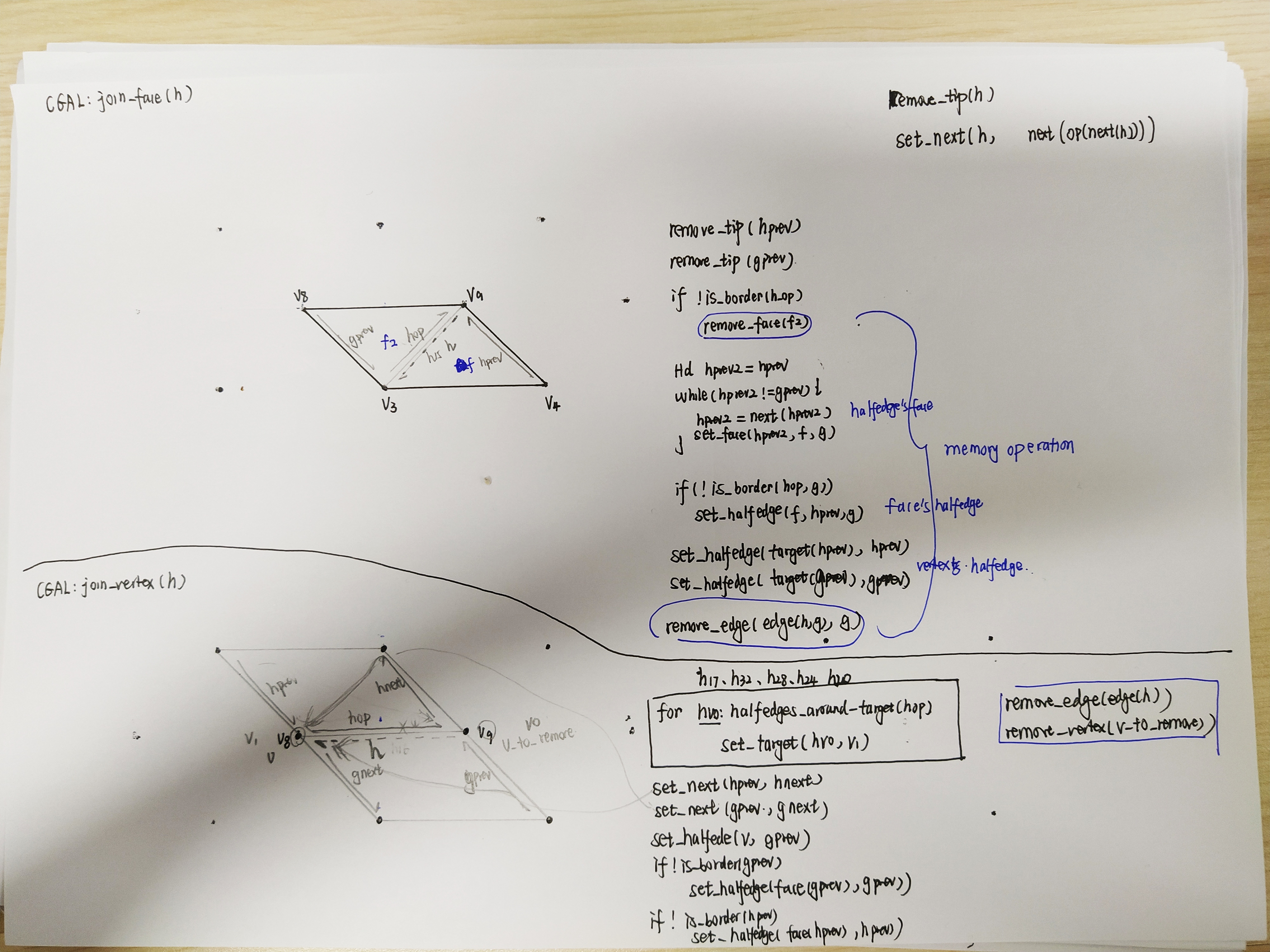
Q-MAT: Computing Medial Axis Transform by Quadratic Error Minimization

Thinking

SkelByMeshContract (contract then collapse) == Q-MAT (find the optimal collapsed position to minimize reonstruct error)

FAQ

1. How to Check whether an edge is valid to be collapsed? is_collapse_ok in QEM

2. addPolyFace patch_relink?

3. How to efficiently compute local average region for triangle mesh?

Refer hw2

Input: mesh (halfedge datastructure)
Output: vUmbrella (local average region, one-ring area)

# mixed voronoi: edge midpoint for obtuse triangle
for f in faces:
    if f.isObtuse:
       for v in fvs:
           if v.isObtuse:
              vUmbrella[v] += 0.5 * fArea
           else:
              vUmbrella[v] += 0.25 * fArea
    else:
        cent = f.circumcenter()
        for v0, v1 in fedgepoints:
            midp = (v0 + v1) / 2
            half_len = 0.5 * (v0-v1).norm()
            areaRightAngTri = (midp-cent).norm() * half_len) /2
            vUmbrella[v0] += 0.5 * areaRightAngTri # !!! multiply 0.5 since each vertex is counted twice
            vUmbrella[v1] += 0.5 * areaRightAngTri # !!! multiply 0.5 since each vertex is counted twice
        

# barycentric: barycenter, edgemidpoints
for f in faces:
    for v0, v1 in fedgepoints:
        vTri = f.area() / 6 # barycenter and edge midpoint split the whole triangle face into 6 equal-size triangles
        vUmbrella[v0] += 0.5 * vTri # !!! multiply 0.5 since each vertex is counted twice
        vUmbrella[v1] += 0.5 * vTri # !!! multiply 0.5 since each vertex is counted twice

4. How to understand laplace operator & efficiently implement it?

Flow-based understanding: divergence of flow. Mean-curvature normal.

Cotagent Laplace vs Uniform Laplace: Cotagent Laplace is linear on plane. (Lf_i)=0 for all interior vertices when positions of vertices are in the plane.

for f in faces:
    for v0, v1 in fes:
        L(v0, v0) -= cot(f, e01) # e01, edge between vertex 0 and vertex 1
        L(v1, v1) -= cot(f, e01)
        L(v0, v1) += cot(f, e01)
        L(v1, v0) += cot(f, e10)

5. relationship between gradient operator G and laplace operator L

Laplace == divergence of gradient. This is a visulization of gradient field on triangle mesh

jingma-git/geometry