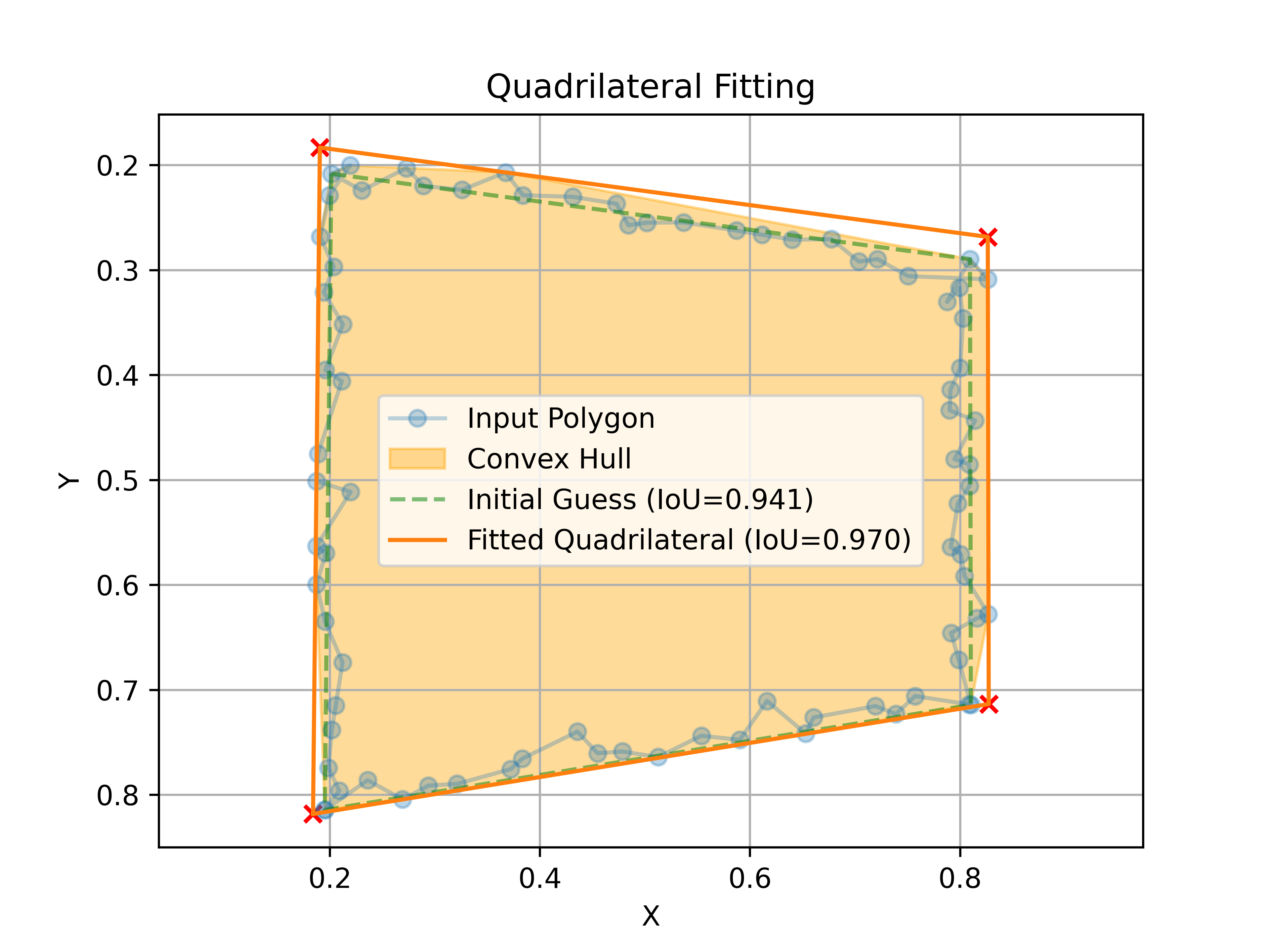
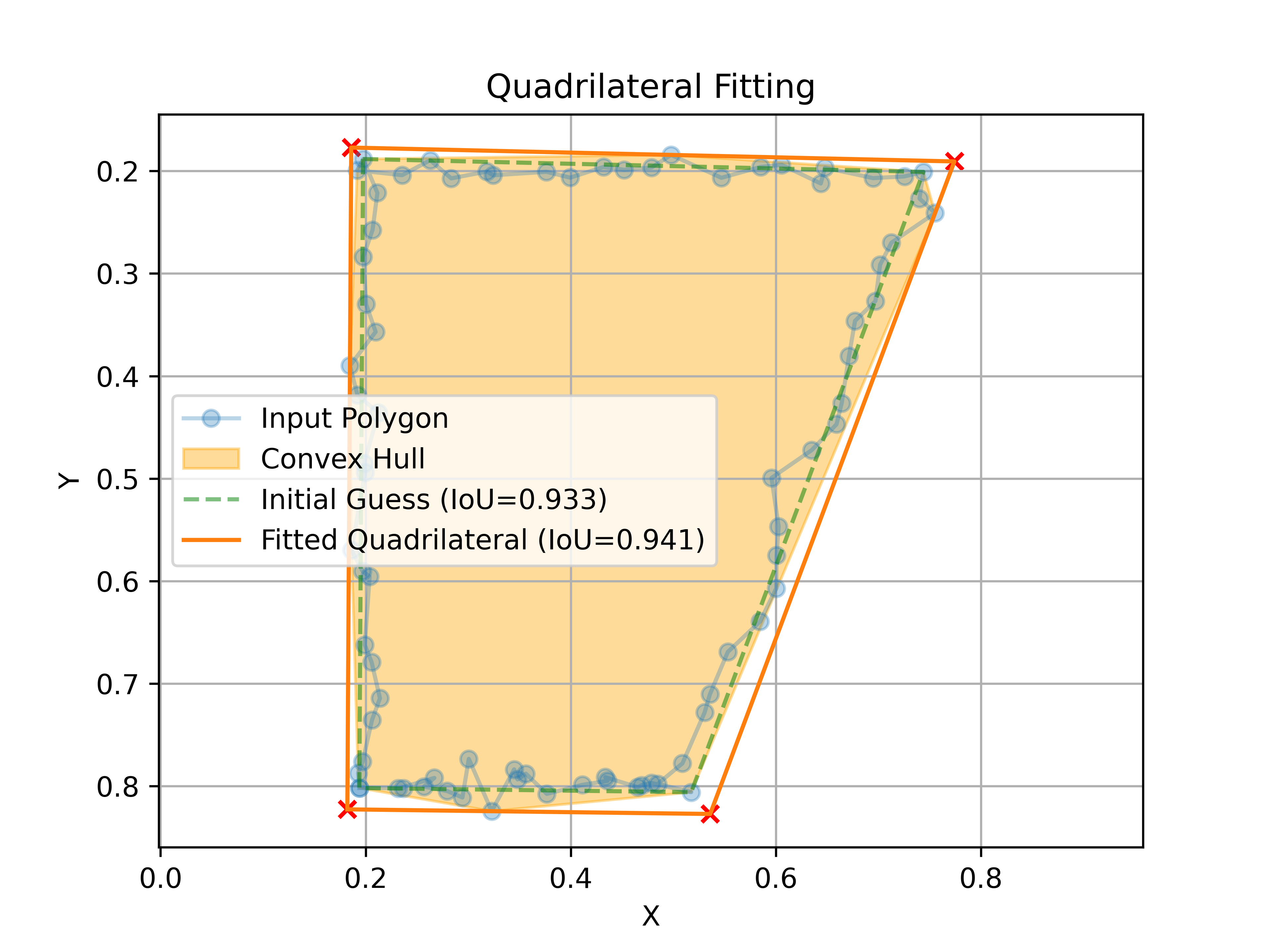
QuadrilateralFitter is an efficient and easy-to-use library for fitting irregular quadrilaterals from polygons or point clouds.
QuadrilateralFitter helps you find that four corners polygon that best approximates your noisy data or detection, so you can apply further processing steps like: perspective correction or pattern matching, without worrying about noise or non-expected vertex.
Optimal Fitted Quadrilateral is the smallest area quadrilateral that contains all the points inside a given polygon.
You can install QuadrilateralFitter with pip:
pip install quadrilateral-fitterThere is only one line you need to use QuadrilateralFitter:
from quadrilateral_fitter import QuadrilateralFitter
# Fit an input polygon of N sides
fitted_quadrilateral = QuadrilateralFitter(polygon=your_noisy_polygon).fit()
If your application can accept fitted quadrilateral to don't strictly include all points within input polygon, you can get the tighter quadrilateral shown as Initial Guess with:
fitted_quadrilateral = QuadrilateralFitter(polygon=your_noisy_polygon).tight_quadrilateralInitialize the QuadrilateralFitter instance..
polygon: np.ndarray | tuple | list | shapely.Polygon. List of the polygon coordinates. It must be a list of coordinates, in the formatXY, shape (N, 2).
simplify_polygons_larger_than: int | None. List of the polygon coordinates. It must be a list of coordinates, in the formatXY, shape (N, 2). If a number is specified, the method will make a preliminar Douglas-Peucker simplification of the internally used Convex Hull if it has more thansimplify_polygons_larger_than vertices. This will speed up the process, but may lead to a sub-optimal quadrilateral approximation. Default: 10.
Returns: tuple[tuple[float, float], tuple[float, float], tuple[float, float], tuple[float, float]]: A tuple containing the four XY coordinates of the fitted cuadrilateral. This quadrilateral will minimize the IoU (Intersection Over Union) with the input polygon, while containing all its points inside. If your use case can allow loosing points from the input polygon, you can read the QuadrilateralFitter.tight_polygon property to obtain a tighter quadrilateral.
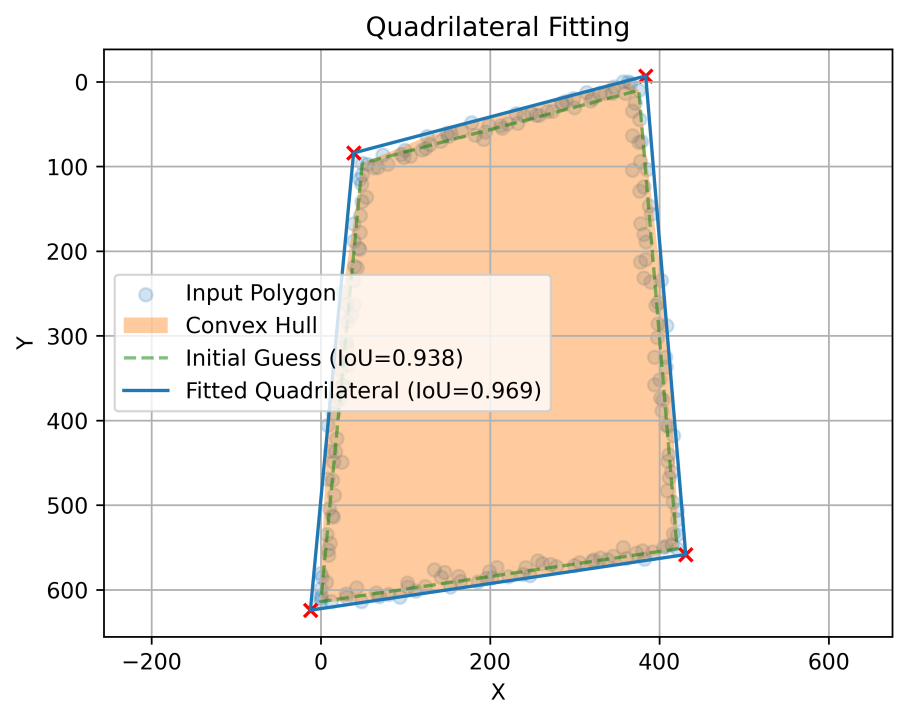
Let's simulate a real case scenario where we detect a noisy polygon from a form that we know should be a perfect rectangle (only deformed by perspective).
import numpy as np
import cv2
image = cv2.cvtColor(cv2.imread('./resources/input_sample.jpg'), cv2.COLOR_BGR2RGB)
# Save the Ground Truth corners
true_corners = np.array([[50., 100.], [370., 0.], [421., 550.], [0., 614.], [50., 100.]], dtype=np.float32)
# Generate a simulated noisy detection
sides = [np.linspace([x1, y1], [x2, y2], 20) + np.random.normal(scale=10, size=(20, 2))
for (x1, y1), (x2, y2) in zip(true_corners[:-1], true_corners[1:])]
noisy_corners = np.concatenate(sides, axis=0)
# To simplify, we will clip the corners to be within the image
noisy_corners[:, 0] = np.clip(noisy_corners[:, 0], a_min=0., a_max=image.shape[1])
noisy_corners[:, 1] = np.clip(noisy_corners[:, 1], a_min=0., a_max=image.shape[0])
And now, let's run QuadrilateralFitter to find the quadrilateral that best approximates our noisy detection (without leaving points outside).
from quadrilateral_fitter import QuadrilateralFitter
# Define the fitter (we want to keep it for reading internal variables later)
fitter = QuadrilateralFitter(polygon=noisy_corners)
# Get the fitted quadrilateral that contains all the points inside the input polygon
fitted_quadrilateral = np.array(fitter.fit(), dtype=np.float32)
# If you wanna to get a tighter mask, less likely to contain points outside the real quadrilateral,
# but that cannot ensure to always contain all the points within the input polygon, you can use:
tight_quadrilateral = np.array(fitter.tight_quadrilateral, dtype=np.float32)
# To show the plot of the fitting process
fitter.plot()
Finally, for use cases like this, we could use fitted quadrilaterals to apply a perspective correction to the image, so we can get a visual insight of the results.
# Generate the destiny points for the perspective correction by adjusting it to a perfect rectangle
h, w = image.shape[:2]
for quadrilateral in (fitted_quadrilateral, tight_quadrilateral):
# Cast it to a numpy for agile manipulation
quadrilateral = np.array(quadrilateral, dtype=np.float32)
# Get the bounding box of the fitted quadrilateral
min_x, min_y = np.min(quadrilateral, axis=0)
max_x, max_y = np.max(quadrilateral, axis=0)
# Define the destiny points for the perspective correction
destiny_points = np.array(((min_x, min_y), (max_x, min_y),
(max_x, max_y), (min_x, max_y)), dtype=np.float32)
# Calculate the homography matrix from the quadrilateral to the rectangle
homography_matrix, _ = cv2.findHomography(srcPoints=quadrilateral, dstPoints=rect_points)
# Warp the image using the homography matrix
warped_image = cv2.warpPerspective(src=image, M=homography_matrix, dsize=(w, h))
