A C++ header only library for decomposition of spectra into a sum of response functions whose weights are positive definite.
DecompLib is a small header only template library for decomposing a spectrum into a set of weighted response functions. The decomposition processes is necessary because the response of a detector to mono-energetic incident radiation is not necessarily mono-energetic, let alone at the same energy. Therefore to determine the radiation incident on the detector the detected spectrum must be decomposed using the response matrix (each row encodes the response to a particular mono-energetic input.)
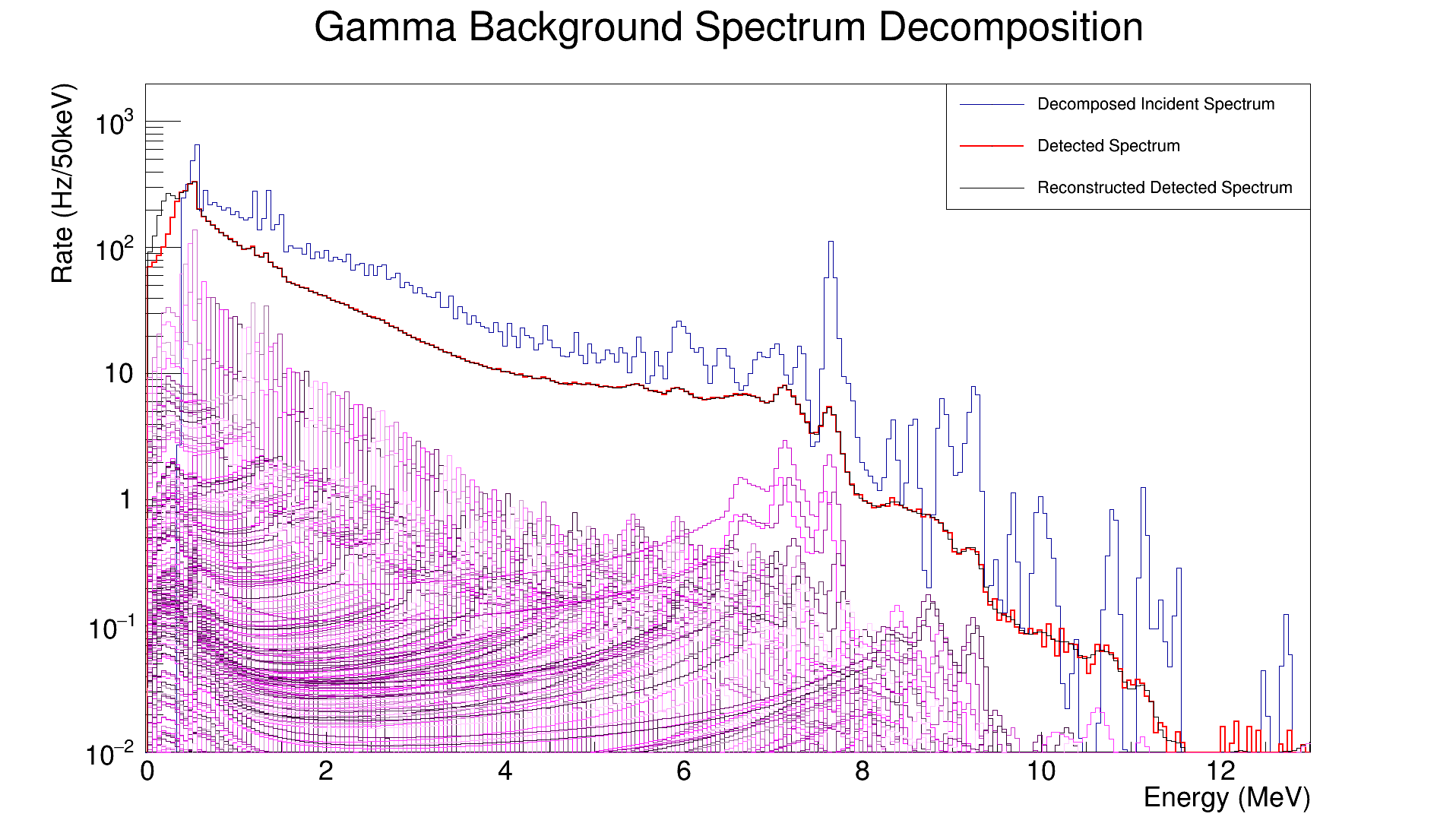
Given a spectrum and response matrix DecompLib can find the incident spectrum (or at least something resembling it) from the weights of the response functions. Below is an example of this done with a spectrum from an NaI(Tl) detector and a response matrix generated by simulating gamma-ray energy deposition in the detector and then convolving the spectrum with the widths extracted from the spectrum (producing an underestimate of the width at high energy in this case).
Here the blue curve is the output of the decomposition algorithm (and the incident spectrum in gammas per second per bin), the black is the algorithm's reconstruction of the input spectrum, the red is original input spectrum, and the curves in varying shades of magenta, pink, and gray are the response functions multiplied by the corresponding weights obtained by the decomposition algorithm (the original response function was normalized to be the "average response to a single gamma ray").
A decomposition can be stated as the following fitting problem:
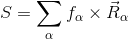 Where
Where S is the input spectrum R_alpha are the rows of the response matrix (response functions), and f_alpha are the weights of the response functions (the incident spectrum). Here though the the various response functions may have a great deal of similarity, causing normal linear algreba methods to fail. The algorithm used in DecompLib will yield positive definite results in a numerically stable fashion. Please see the second half technical report in the DecompLib doc directory for more details.
I ask that if you use DecompLib in work that you are publishing, that you cite it.
Because DecompLib is a header only library it is unnecessary to build anything prior to installing it. The only things that need to be built are the documentation and the example. The next section tells how to build the example and documentation, if you merely wish to install the headers and start using them you can skip straight to the install subsection
If you wish to only build the example and its attendant utilities you need only run make example. Contrariwise, if you wish to only build the documentation simply run make doc. To make both the example and documentation simply run make all or make. This will then build the Example program and the three associated utilities with it. Then it will build the documentation, running doxygen which outputs html and LaTeX, building the doxygen LaTeX output, then building the LaTeX technical report.
Installation of DecompLib is fairly easy, but . In most unix systems you need only decided if you wish to install the library globally across the whole system (requires sudo or root permissions) or if you want to install the library locally.
If you wish to install system wide:
-# Verify that /usr/include is the correct system header location.
- If it is not correct, edit the line containing
Global_Header_Loc=/usr/includeto the correct location -# Runsudo make install
If you wish to install locally: -# Determine your preferred local install location.
- If you do not wish to install to
${HOME}/includeedit the line containingLocal_Header_Loc=~/includeto the prefered location. -# Runmake local_install
Usage of the library is simple. One need only instantiate one of each of the three classes, fill them with data, then call the performDecomposition function to decompose the spectrum. Since code is worth more than prose for this a semi-pseudocode example is below.
int numberDataBins = X;
DataVector<double> inputSpectrum(numberDataBins, writeErrorMsgs);
//loop to set the inputSpectrum bin values with setElement(bin#, value)
int numberResponseFunctions = Y;
RespMatrix<double> responseMatrix(numberResponseFunctions, numberDataBins, writeErrorMsgs);
//nested loop to set the response matrix values with setElement(responseFunction#, bin#, value)
DecompVector<double> parameterSet(numberResponseFunctions, writeErrorMsgs);
parameterSet.initWithConstant(initialValue);
//now call performDecomposition
long long retVal = performDecomposition(inputSpectrum, responseMatrix, parameterSet);Documentation is available in a few forms. For the full documenation of DecompLib's objects and functions please see https://jmatta1.github.io/DecompLib/ or generate the doxygen documentation within the doc directory. For more about usage of the algorithm itself and the potential alternative uses and pitfalls associated with it, see the second half of the technical report in the doc directory.
DecompLib contains a directory called Example. This directory contains a program demonstrating the usage of DecompLib as well as four utility functions to assist with the input and output to the example.
The Example/DecomposeSpectrum subdirectory contains the actual usage example. In addition to the program decompose it contains a sample input spectrum in csv format and a sample response matrix in a gzip compressed csv format (it will need to be uncompressed for use). After being built you can run the example as follows ./decompose <spectrumCsvFile> <responseMatrixCsvFile> <outputFileBase>.
Notes: outputFileBase is prefixed onto "_init.csv" (the initial decomposition values spectrum), "_final.csv" (the final decomposition values spectrum), "_sum.csv" (the sum of response functions from the matrix weighted by the final decomposition values), and "_resid.csv" (the weighted sum subtracted from the input spectrum).
Before decompose performs the decomposition it asks several quesions about the parameters that go into the decomposition. How to set the initial DecompVector guess, what is the threshold for ignoring parameters when checking convergence, what is the convergence criterion. It also asks what limits of bin numbers it should use for the spectrum and response matrix. For the sample response matrix and spectrum included the X-axis limits that will pass the safety checks are [0, 3049] and the Y-axis limits that will pass the safety checks are [4, 1499], narrower limits can be chosen, but not broader. Additionally, the X-axis limits for the response matrix and the limits for the spectrum should always be the same.
The Example/RootTh1ToCsv contains a utility that will take a root file and the name of any TH1(F,D,I...) in that file and output it to a specified csv format file. After being built it can be invoked as follows: ./convert1d <inputRootFile> <Th1Name> <outputFile>
The Example/RootTh2ToCsv contains a utility that will take a root file and the name of any TH2(F,D,I...) in that file and output it to a specified csv format file. After being built it can be invoked as follows: ./convert2d <inputRootFile> <Th2Name> <outputFile>
The Example/CsvToRootTh1 contains a utility that a 1D histogram in a csv file and write it into TH1D format in a root file you select. After being built it can be invoked as follows: convert1dCsv <1dHistogramCsv> <outputRootFile> <Th1Name>
The Example/CsvToRootTh1 contains a utility that a 2D histogram in a csv file and write it into TH2F format in a root file you select. After being built it can be invoked as follows: convert2dCsv <2dHistogramCsv> <outputRootFile> <Th2Name>
This is a greatly expanded version of the usage pseudocode from above. It includes comments explaining more about choices as well as showing where default parameters were chosen in function calls above.
//decide what floating point type will be used for everything
typedef double fp_type;
//Safety checks (looking for bad inputs etc) can output messages to std::cout if
//true is passed for certain parameters, look for this boolean in declarations and calls below
bool writeErrorMsgs = true;
//make the DataVector which contains the input spectrum
int numberDataBins = X;
DataVector<fp_type> inputSpectrum(numberDataBins, writeErrorMsgs);
//set the data vector
for(int i=0; i<numberDataBins; ++i)
{
inputSpectrum.setElement(i, SpectrumDataSource.GetBinContent(i));
}
//make the RespMatrix which response matrix with which to do the decomposition,
//it must have the same number of bins per response function as the input spectrum has bins
int numberResponseFunctions = Y;
RespMatrix<fp_type> responseMatrix(numberResponseFunctions, numberDataBins, writeErrorMsgs);
for(int i=0; i<numberResponseFunctions; ++i)
{
for(int j=0; j<numberDataBins; ++j)
{
responseMatrix.setElement(i, j, ResponseFunctionArray[i].GetBinContent(i));
}
}
//make the DecompVector which will hold the initial guess, it must have as many bins
//as there are response functions in the RespMatrix
DecompVector<fp_type> initGuess(numberResponseFunctions, writeErrorMsgs);
//there are two options to initialize a DecompVector beyond simply setting every bin
//you can pass it a filled input spectrum along with an offset and scaling factor
//it will then fill it self with an offset and scaled sub sampling of the input spectrum
//this is accomplished using the initWithDataVector member function
initGuess.initWithDataVector(*inputSpectrum, scalingFactor, offsetValue);
//you can also initialize the DecompVector to a constant value. This is recommended
//as it seems to encode less noise into the final result
//this is accomplished using the initWithConstant member function
initGuess.initWithConstant(initialValue);
//because we may want to keep the initial guess on hand and the initial guess
//passed to performDecomposition is overwritten with the final result, we use the
//copy constructor of DecompVector in order to have two copies, one to keep and
//one to pass to performDecomposition
DecompVector<fp_type> parameterSet(initGuess);
//Here I set the value below which a parameter is not considered when determining
//if the algorithm has yet converged. This is useful because for very small number
//the nature of floating point math is that they will start to change very quickly
//especially if the algorithm is moving them towards zero (though it will never reach
//there). The exact value of this will depend on the nature of the spectra you are
//decomposing 1e-6 works in the sample spectrum and response matrix included with
//with the Example
fp_type minConvThresh = 1.0e-6;
//Here I set the maximum fractional change that a parameter can show between
//iterations before it is declared unconverged, I am uncertain if good values
//for this will change with different problems. I suspect that it will, but that
//the changes will be small compared to the changes that can occur in minConvThresh
fp_type convergenceCriterion = 0.005;
//now call performDecomposition
long long retVal = performDecomposition(inputSpectrum, responseMatrix,
parameterSet, minConvThresh,
convergenceCriterion, writeErrorMsgs);
//if retVal is not negative, it contains the number of iterations required for convergence
//if retVal is negative then there was an error and the decompositon was not performed
//if the decomposition was run then you can retrieve the results using the DecompVector
//member function `getElement(binNumber)`