rt-cqt aims to be a reasonable fast, header-only C++11 library for performing the Constant-Q Transform (CQT), optimized for real-time audio applications. It supports dynamic handling of different block sizes and sample rates, making it ideal for scenarios with varying audio processing demands. The library offers two distinct implementations:
- Constant-Q Transform (include/ConstantQTransform.h): This version performs a Fast Fourier Transform (FFT) for each octave.
- Sliding Constant-Q Transform (include/SlidingCqt.h): This version minimizes latency by continuously updating frequency bins with every new audio sample, making it particularly suitable low-latency applications.
Both implementations utilize polyphase IIR lowpass filters for efficient upsampling and downsampling, which reduces computational overhead by processing lower octaves at reduced sample rates.
The implementation is roughly based on the Judith C. Brown, Miller S. Puckette: An efficient algorithm for the calculation of a constant Q transform paper. pffft is used to handle the ffts.
An example can be found in examples/cqt.cpp.
Even though this library is header-only, the pffft implementation is not. Hence, the following files have to be linked into your project:
submodules/pffft/pffft.c
submodules/pffft/pffft_common.c
submodules/pffft/pffft_double.cWhile the regular Constant-Q Transform performs an FFT for each octave and hop, the CQT can also be implemented in a sliding manner, where the hop size is effectively reduced to 1 sample. The implementation follows Russell Bradford, John ffitch, Richard Dobson: SLIDING WITH A CONSTANT Q. Since this method does not rely on FFTs, the implementation remains lightweight, header-only, and free from external dependencies like pffft.
An example can be found in examples/scqt.cpp.
This is WIP. Python bindings can be found in the python-bindings folder, using pybind11.
CQT Analyzer Audio-Plugin based on iPlug2
WIP Reverb plugin operating in Sliding CQT domain
- While the Polyphase IIR lowpasses are cheap, they distort the phase of the signal. For future, a linear phase approach could be added.
- Amplitudes in CQT domain, as well as for the re-synthesized signal for Sliding CQT are quite low, especially when using the windowed version. WIP to find out why and how to fix it.
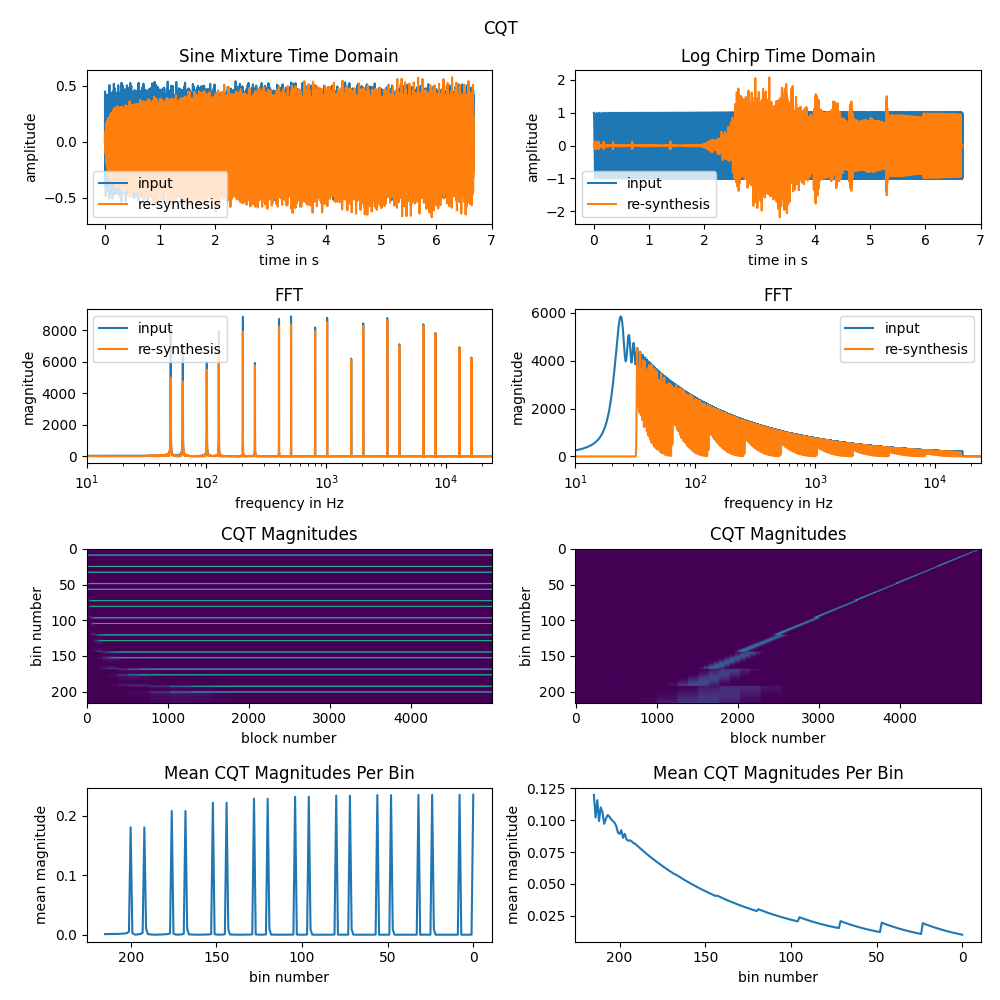
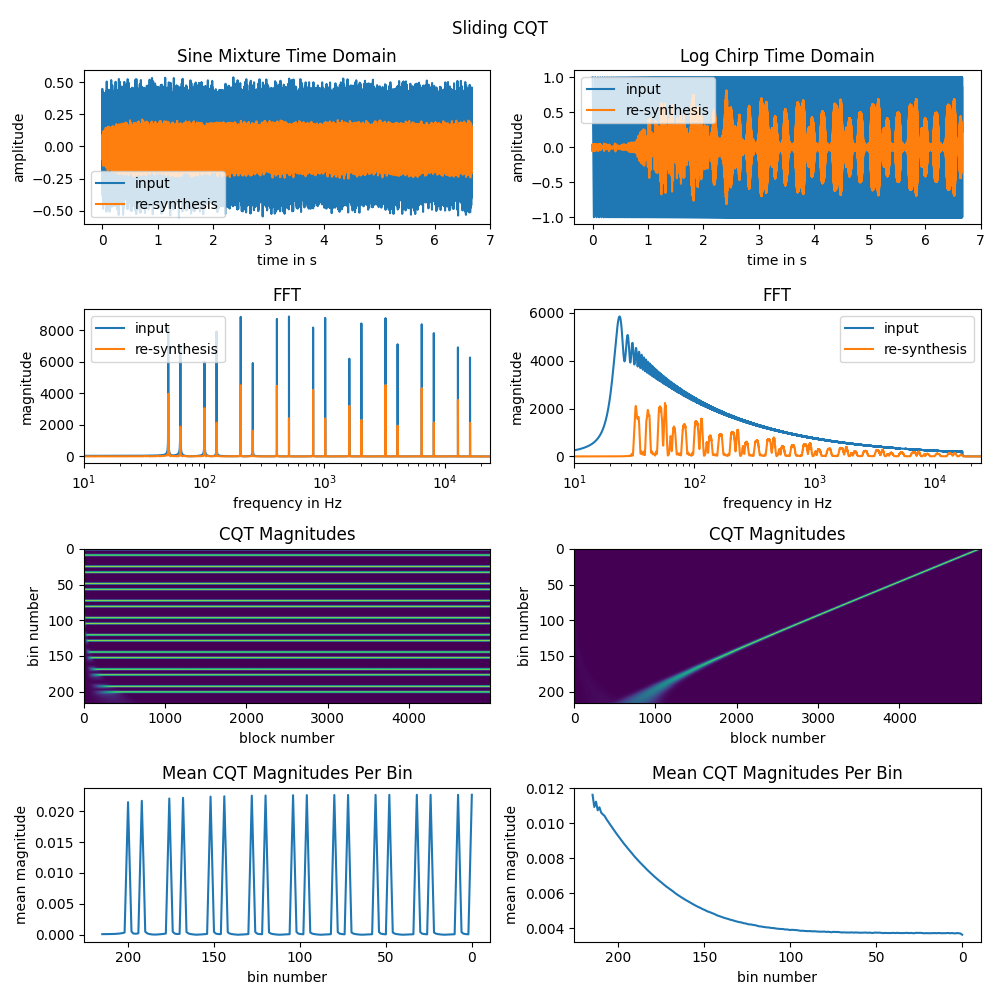
For illustration of the current status, python binds are used to create some plots (python-bindings/examples/illustration.py).
- 24 bins per octave, 9 octaves and a block size of 64 samples.
- Two different input signals. A mixture of sine tones (note c and e with equal amplitude across all octaves) and a logarithmic sine chirp.
- Lower latency of the sliding transform becomes quite visible for the chirp input signal. CQT with big hop sizes can't properly resolve the low frequencies of the chirp.
- Amplitudes of the sliding transform are quite low.
- Re-synthesis for both approaches is not perfect. Especially for the chirp signal, phase is distorted quite heavily. FIR lowpass filters for downsampling might help here.