sentential: A Python repository from joedougherty

SENTENTIAL

An interpreter for sentential logic (propositional calculus) written in Python.

A work in progress.

sentential can help you:

Generate truth tables

from sentential import Proposition
law_of_non_contradiction = Proposition('''¬(p & ¬p)''')
law_of_non_contradiction.pretty_truth_table()

p	¬(p & ¬p)
True	True
False	True

# Propositions can be combined with standard string operators
law_of_non_contradiction = Proposition('''¬(p & ¬p)''')
law_of_excluded_middle = Proposition('''(p v ¬p)''')

the_nature_of_bivalence = Proposition('{} <-> {}'.format(law_of_non_contradiction, law_of_excluded_middle))

the_nature_of_bivalence.pretty_truth_table()

p	¬(p & ¬p) <-> (p v ¬p)
True	True
False	True

# Inspect the internal representation
law_of_non_contradiction.truth_table()

# Results in:
[OrderedDict([('p', True), ('expr_truth_value', True)]),
 OrderedDict([('p', False), ('expr_truth_value', True)])]

Determine if a proposition is a theorem/contradiction

law_of_non_contradiction.is_theorem() # True

negated_lnc = Proposition('''¬(¬(p & ¬p))''')

negated_lnc.is_contradiction() # True

Find the CNF (Conjunctive Normal Form) expression of a proposition

from sentential import Proposition

prop = Proposition('''((p and w) -> !e)''')

prop.cnf() # [{'~e', '~p', '~w'}]

sentential can also help you find proofs (by resolution).

from sentential import Proposition
from sentential.KnowledgeBase import KnowledgeBase

kb = KnowledgeBase()

# Let's verify that we can run a proof using hypothetical syllogism
# (https://en.wikipedia.org/wiki/Hypothetical_syllogism)
kb.add_axiom(Proposition('''a -> b'''))
kb.add_axiom(Proposition('''b -> c'''))
kb.add_axiom(Proposition('''c -> d'''))

# Let's say we know it's the case that "a"
kb.add_axiom(Proposition('''a'''))

# Can we construct a proof that "d" is true (given what we know above)?
kb.add_goal(Proposition('''d'''))

# Indeed we can. A proof was found!
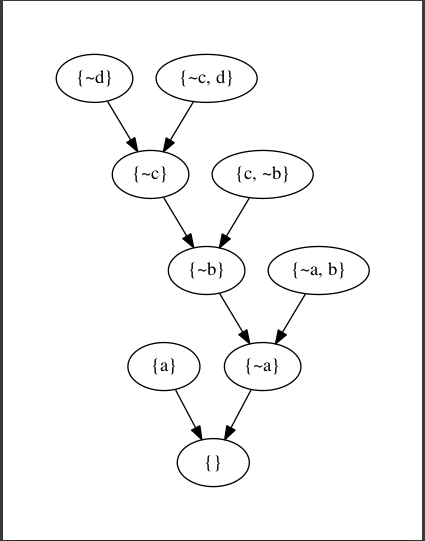
kb.prove() # True

Proofs can be inspected further...

proof = kb.most_recent_proof()

# Inspect the proof steps taken to arrive at the empty clause
proof.steps

# If you have graphviz installed, you can try generating
# an image demonstating the proof as a graph
proof.visualize()

SYNTAX

sentential was designed to allow you to express propositions using the familiar symbols of classical logic.

The parser strives to minimize the user's mental overhead in converting his or her logical expressions into statements readable by sentential.

Here are some examples of legal expressions one could use to instatiate a Proposition:

"""p"""
"""p v q"""
"""(p v q)"""
"""¬((a -> s) iff (!w and r))"""
"""!¬(q)"""

Double negation is supported. Most operations can be expressed with multiple symbols. You can use ¬ just as easily as ! or ~. Mix and match as you please.

Symbol	Operation
¬	Not
~	Not
!	Not
v	Or
or	Or
&	And
and	And
->	if-then (conditional)
iff	if and only if (biconditional)
<->	if and only if (biconditional)
=	if any only if (biconditional)

It is important to bear in mind that all sub-expressions may contain at most two terms and one binary operator.

Examples:

'''(p v q)'''       # Two terms:   ("p","q")        | One binary operator: "v"  | OK!
'''p'''             # One term:    ("p")            | Zero binary operators     | OK!
'''(p & q & r)'''   # Three terms: ("p","q","r")    | Two binary operators      | ERROR!!!

While it may occasionally be inconvenient to nest expressions with shared operators, this provides unambiguous grouping rules. What you lose in convenience, you gain in semantic precision.

The last example can be expressed: Proposition('''((p & q) & r)''') or Proposition('''(p & (q & r))''')

You can even use sentential to verify these expressions are equivalent:

p1 = Proposition('''((p & q) & r)''')
p2 = Proposition('''(p & (q & r))''')

prop = Proposition('{} = {}'.format(p1, p2))

prop.is_theorem() # True

joedougherty/sentential

SENTENTIAL

SYNTAX