Generative Expressions

Generative Expressions (Geex) is a code generation tool for writing high-level Clojure code that generates fast low-level code.

Example

Here is an implementation for computing the square-root of a number using Newton-Raphson:

(ns examples.sqrt-test
  (:require [geex.common :as c]
            [geex.java :as java]
            [geex.core :as gx]
            [clojure.test :refer :all]))

(defn sqrt-iteration [k x]
  (c/- x (c// (c/- (c/* x x) k)
              (c/* 2.0 x))))

(java/typed-defn unrolled-sqrt [Double/TYPE x]

                 ;; Display time and generated code:
                 (gx/set-flag! :disp :disp-time :format)
                 
                 (->> x
                      (iterate (partial sqrt-iteration x))
                      (take 10)
                      last))

which results in a function unrolled-sqrt that we can call:

(unrolled-sqrt 2.0)
;; => 1.4142135623730951

This is the code that was generated in order to produce this function:

package examples_psqrt_dtest;

public class TypedDefn__unrolled_dsqrt {
  /* Various definitions */
  public double apply(final double arg00) {
    final double s0012 = (arg00 - (((arg00 * arg00) - arg00) / (2.0 * arg00)));
    final double s0018 = (s0012 - (((s0012 * s0012) - arg00) / (2.0 * s0012)));
    final double s0024 = (s0018 - (((s0018 * s0018) - arg00) / (2.0 * s0018)));
    final double s0030 = (s0024 - (((s0024 * s0024) - arg00) / (2.0 * s0024)));
    final double s0036 = (s0030 - (((s0030 * s0030) - arg00) / (2.0 * s0030)));
    final double s0042 = (s0036 - (((s0036 * s0036) - arg00) / (2.0 * s0036)));
    final double s0048 = (s0042 - (((s0042 * s0042) - arg00) / (2.0 * s0042)));
    final double s0054 = (s0048 - (((s0048 * s0048) - arg00) / (2.0 * s0048)));
    return (s0054 - (((s0054 * s0054) - arg00) / (2.0 * s0054)));
  }
}

Getting started

Geex can be obtained as a Maven dependency, so in your Leiningen project, you just have to add the line

[geex "0.11.0"]

Tutorial

There is a work-in-progress and incomplete tutorial that you can read.

You can also try it out by cloning this repository and looking at the examples, such as

How to compute the square root using Newton-Raphson
Forward-mode automatic differentiation
Circle fitting
Expression templates on vectors à la C++
More matrix operations (without expression templates).
Covariance matrix computation.
Another circle fitting example making use of operator overloading.
Naïve N-body simulation.

Benchmark

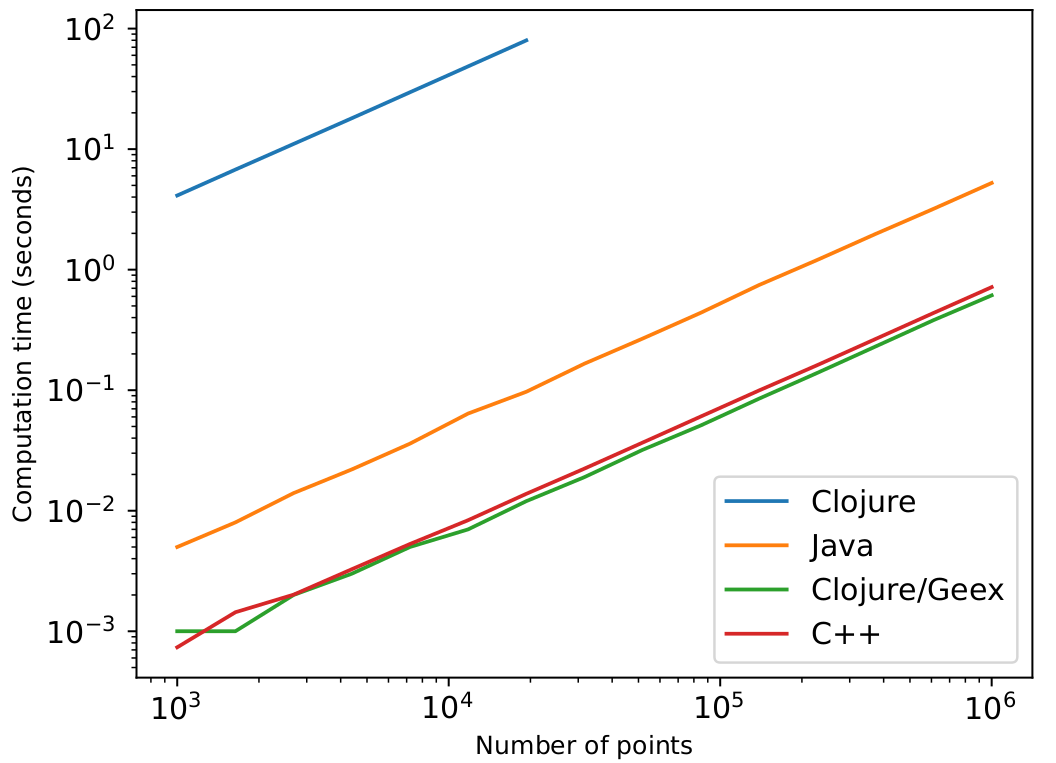
To assess the effectiveness of this approach, we tried to estimate the parameters of a circle (centre x and y position, and radius) from a set of 2D observations. We do this by formulating an objective function that is minimized using gradient descent. The gradient is computed using forward mode automatic differentiation.

This algorithm was implemented in high-level Java, C++, and Clojure (with and without Geex). The computation times were measured for varying numbers of points to which we fit the circle parameters.

Plotting the computation time as a function of number of circle points results in this plot:

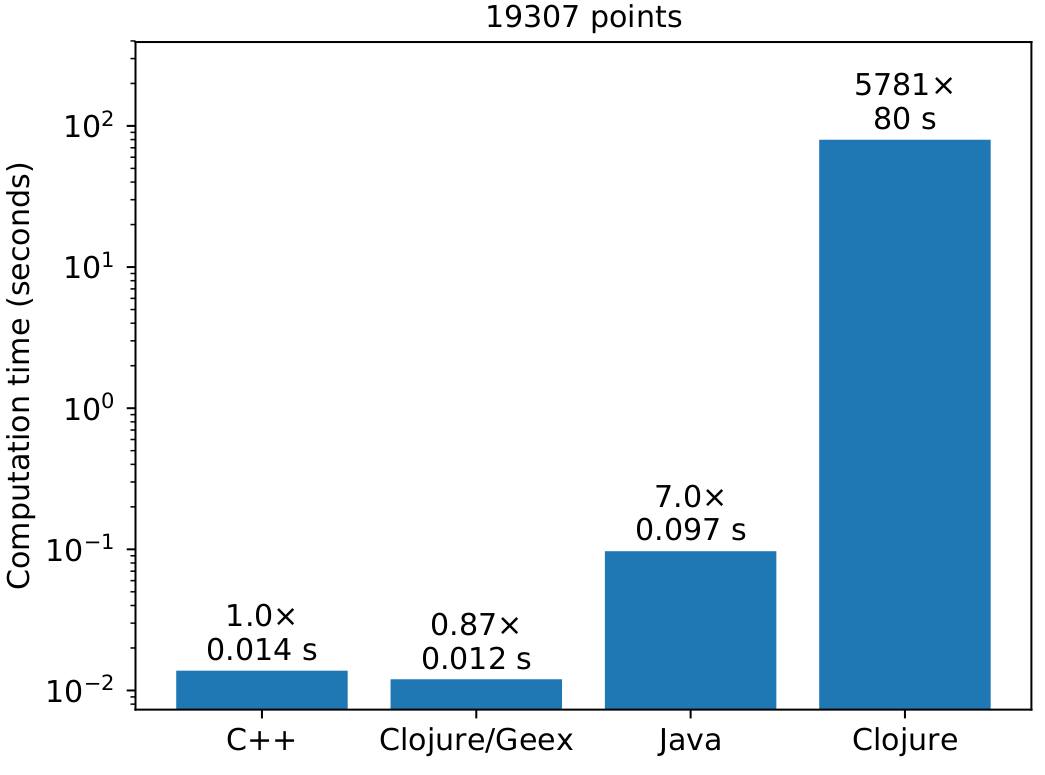
Specifically, for 19307 points, we get these computations times:

Please note that these tests measure high-level implementations that have not been optimized. There is room for error. You may get other results than I do, depending on your setup.

API Reference

The API reference documentation can be found at cljdoc.org.

Module structure

If you add [lein-ns-dep-graph "0.2.0-SNAPSHOT"] to your Leiningen plugins, this graph can be generated using lein ns-dep-graph:

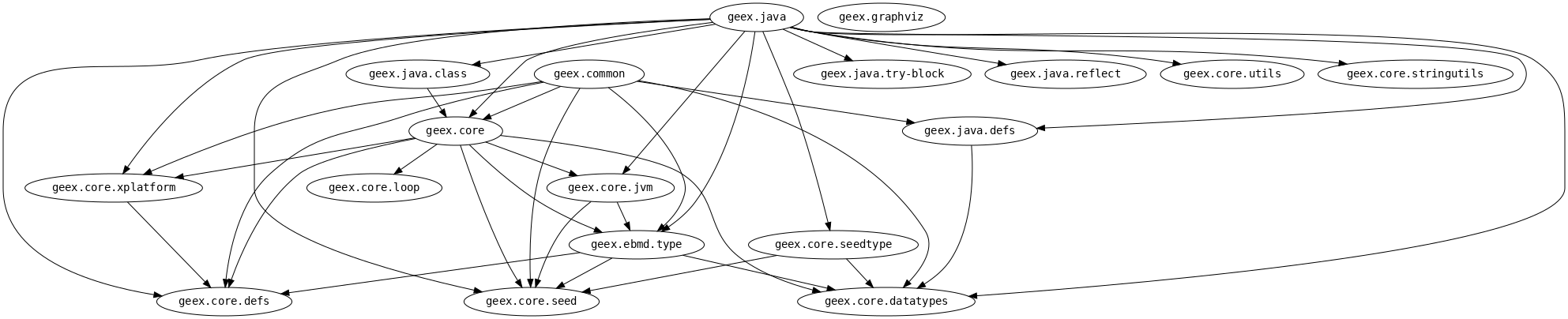
geex.core contains the core components of code generation and analysis.

geex.common is a library of common operations.

geex.java contains specific support for the Java platform.

Contributions

You can contribute by filing bug issues. Fixing minor issues such as failing builds for different platforms is also important.

License

Distributed under the Eclipse Public License either version 1.0 or (at your option) any later version.

jonasseglare/geex