Note: It will take 2-5 minutes for the points to update after you push.

Late Days: I am using 0 late days

Warning

START EARLY. I cannot stress this enough. On average it takes 5-7 days for students to complete the dictionary. The boggle solver can also take 5-7 days.

Boggle solver cannot work with the Dictionary so be sure to make sure the Dictionary works before moving onto the Boggle solver.

Deliverables

Deliverable	Points
Dictionary_Tests	35
Boggle_Tests	30
Questions	15
Commits	10
Commenting	10
Total	100

The same standards for committing and commenting apply for this assignment as previous assignments. You should have pre/post comments in the header files at minimum as well as general comments. You should also be committing and pushing regularly.

Questions (3 pts/question)

The dictionary implementation given assumes each word is a lowercase letter from "a" to "z". Suppose you were to change the implementation of the dictionary to include any unicode character. How would you change the Node definition to accommodate the extra characters?
```
class Node {
 // Your answer here
 isWord=false;
 for(int i=0;i<127;++i){ //Make all nodes to null
 children[i]=NULL;
 }
};
```
Suppose you use a binary search tree to store the words from the dictionary.txt file. In the worse case scenario, how many comparisons would it take to find out if a word is in the dictionary?

O(n^2) where n is the length of a word
Suppose you use a prefix tree to store the words from the dictionary.txt file. In the worse case scenario, how many comparisons would it take to find out if a word is in the dictionary using the Dictionary class?

O(log n)
Why is the prefix tree better than a binary search tree for implementing Boggle?

Time complexity is lesser for Prefix tree when compared to Binary Search tree.
Suppose you do not use IsPrefix in your SolveBoard implementation.
How would that affect the program?

if (!dict.IsPrefix(word)) return;

Recommended Implementation Order

Dictionary Class (Part A)

This is the recommend implementation order for the Dictionary class.

Dictionary()
WordCount()
AddWord(string word)
IsWord(string word)
IsPrefix(string word)
LoadDictionaryFile()
Dictionary(string filename)
SaveDictionaryFile(string filename)
MakeEmpty()
Dictionary& operator=(const Dictionary& otherDict)

Boggle Class (Part B)

This is the recommended implementation order for the Boggle class.

The Dictionary class needs to work!
Boggle()
SetBoard(string board[BOARD_SIZE][BOARD_SIZE])
SolveBoard(printBoard, outfile)/SolveBoardHelper

Boggle Solver

The Boggle board is a 4x4 grid onto which you shake and randomly distribute 16 dice. These 6-sided dice have letters rather than numbers, creating a grid of letters from which you can form words. In the original version, the players start simultaneously and write down all the words they can find by tracing by a path through adjoining letters. Two letters adjoin if they are next to each other horizontally, vertically, or diagonally. There are up to eight letters adjoining a cube. A grid position can only be used once in the word. When time is called, duplicates are removed from the players' lists and the players receive points for their remaining words based on the word lengths. In this assignment, you will be creating a program that will find all the words on a boggle board. Any word found in the dictionary will count as a word on the boggle board.

Boggle Game: https://www.youtube.com/watch?v=BJAdXnGAb7k

This assignment is broken into two parts. The first part of the program will be creating a dictionary that can be used to store and look up words. This dictionary implementation will use a special tree called a prefix tree.

Part A: Dictionary

To store the words in this assignment, you will be creating dictionary using a data structure called a prefix tree (also known as a Trie). This data structure allows for the quick lookup of whether or not a word is valid. It will also allow you to find all words with a specific prefix. Rather than store each word individually, we instead store the words using a tree:

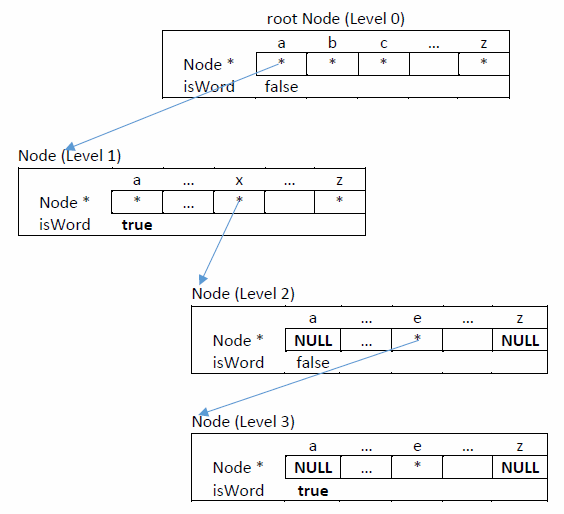
The example above shows two how the words "a" and "axe" are represented using a tree.

Each node holds 26 pointers to other nodes; each of these nodes corresponds to a specific letter.
Each node also holds a single boolean flag.
Essentially, each word is represented by a path down the tree.
If the path ends with a "false", then the path does not represent a valid word.

For example, the root node has a path from the first Node* pointer (i.e. the pointer representing 'a') to another Node. Notice that this first level node has a "true" flag. This indicates that "a" is a valid word. If we examine the pointer for the second level "x" position, we find that a path exists for "ax" to another node. When we examine this second level node, we find that the pointer for the 'a' position is NULL. This indicates that "aa" is not a valid word or prefix. If we examine the pointer for the 'e' position, we see that another node exists. When we look at this 3rd level node, we find that the flag for this position is true; this make sense since "axe" is a valid word. Notice that the 'a' Node pointer at the third level is NULL; this means that there is no word with a prefix of "axea". Similarly, since the node for 'z' at the third level is NULL, this means there is no word with the prefix "axez".

HINT: I highly suggest using the following tool to help you get a feel for how the data structure works.

https://www.cs.usfca.edu/~galles/visualization/Trie.html

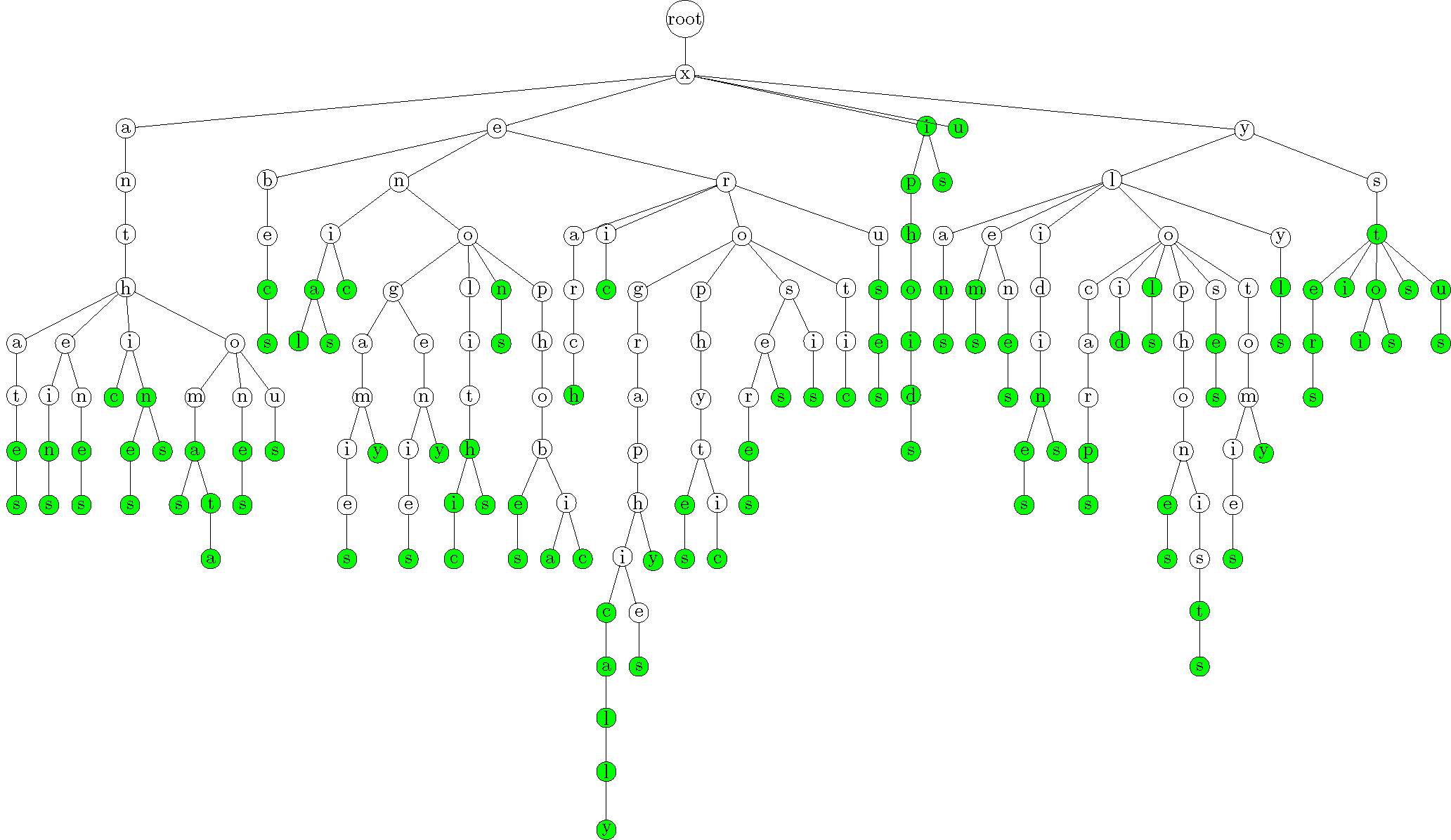
Bigger Example: This is an example of the prefix tree with all of the words starting with the letter x from the boggle dictionary. The green nodes indicates that the path to that node is a word. For example, "xebec" is a word. (See the trie_x.pdf in the readme_images folder for a higher resolution image).

Prefix

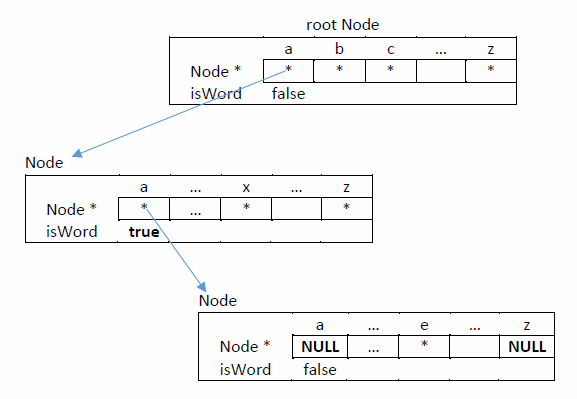
A prefix is a valid path down the tree. A prefix may or may not be a valid word. For the example below, "a" and "ax" are valid prefixes since there are words starting with these letters. However, "aaa" is not a valid prefix. This because the path ends with a NULL.

`Basic_Dictionary.cpp`

The Basic_Dictionary.cpp can be used for development. It will not be used for grading. I suggest using this program first before running the Dictionary_tests.

Note: This program is a CMake Application. It will not show up as a Catch Application.

`struct Node`

Your Node structure should contain an array of pointers. The node can be a struct or class. The size of the array should be NUM_CHARS (ie 26). The struct/class should also contain a boolean flag called isWord to indicate if the path to this node represents a word.

HINT: You may want to consider having a default constructor for your node. This will decrease the amount of code you will need later. You can create a default constructor for a struct the same way you would for a class.

`Dictionary() Default Constructor`

The default constructor should establish a root node and make each position of the branch array null. It should also set the root isWord to false. The total number of words should be 0.

Hint: Having a default constructor for your node will reduce the code required for this function and other functions.

`Dictionary(const Dictionary& otherDict)`

The copy constructor should copy all of the contents of otherDict to this. You should use the copyOther function to accomplish this.

Hint: Be sure to refer to the BinaryDictionaryTree example.

`Dictionary& operator=(const Dictionary& otherDict)`

This overload should copy all of the contents of otherDict to this. You should use the copyOther function to accomplish this.

Hint: Be sure to refer to the BinaryDictionaryTree example.

`copyOther(const Dictionary& otherDict)`

This function should copy all of the values from otherDict to this instance of the dictionary. It will serve as a wrapper for copyHelper in a similar way we recursively copied a binary tree in class. The only difference is we have 26 children instead of two. Here is a rough algorithm:

copyOther(const Dictionary& otherDict):
  Make this of the instance empty
  copy over the numWords from otherDict
    
  for each letter
     call copyHelper with the correct parameters
     
  return this instance

copyHelper(Node*& thisTree, Node*& otherTree):
    This code is very similar to a binary tree.
    The only difference is you need to copy 26 branches
    instead of 2 branches.
    Make sure you also copy the isWord parameter over too.

WARNING: DO NOT JUST SET THE ROOTS EQUAL!

In other words, DO NOT do the following:

root = otherDict.root; // DON'T DO THIS!!!

This will cause both dictionaries to share the same root!

`void MakeEmpty()`

The MakeEmpty function should destroy all the nodes in the tree. After destroying all the nodes in the tree, the root should be remade and the number of words should be set back to 0. MakeEmpty mainly serves as a wrapper function for the destroyHelper. The MakeEmpty and destroyHelper functions work very similarly to the binary tree deconstructor covered in class. The only difference is that you need to destroy 26 branches before deleting the current node.

`Dictionary(string filename)`

This constructor should establish a root node similar to the default constructor. After that, it should open the file filename and add all the words in this file to the dictionary.

HINT: There may be a function that you already wrote to help you with this. This constructor should have very few lines of code.

`void LoadDictionaryFile(string filename)`

This function should open the file filename and add all the words in this file to the dictionary. This function does NOT reset the words in the dictionary. It just adds to the words already in the tree.

`void SaveDictionaryFile(string filename)`

The SaveDictionaryFile function should use a recursive function to find every word in the tree and save it to a file. This function mainly serves as a "Wrapper" for the SaveDictionaryHelper function. The following is a rough algorithm:

SaveDictionaryFile(filename):
  Open the file
  if the file fails to open:
     throw a DictionaryError with the message filename+"failed to open"
  
  Call SaveDictionaryHelper with the appropriate arguments

HINT: What should the prefix be at the root? A path down the tree represents a word. If you have a path that ends at the root node, what word does that represent? Think about this when you set your prefix in the first call to SaveDictionaryHelper called in SaveDictionaryFile.

SaveDictionaryHelper(curr, currPrefix, outFile):
  Basecase (for you to figure out)
  
  if the current node represents a word
     output the word to the file
  
  for each letter:
     Call SaveDictionaryHelper with the appropriate arguments

HINT: How should the prefix change in each call to SaveDictionaryHelper? Be sure to look at how we tracked the path in the maze example. This strategy can also work here.

`void AddWord(string word)`

This method adds a word to the tree. This is accomplished by reading the word character by character and creating a path in the tree for the word if it doesn't exist. Below is the pseudocode for this method:

currNode = root;
for (each character c of the word) {
   if  (the branch for character c is NULL) {
      set the branch of character c = new Node.
      set flag of this new Node to false
   }
   currNode = the pointer index of character c
}
Set the flag at the currNode to true

Here is some code that will help you loop through each character of a string.

// How to loop through each letter of a word
string str = "hello";
for (int i = 0; i < str.size(); i++) {
   cout << str[i] << endl;
}

While processing the characters, if you encounter a character that is not between 'a' and 'z', you should throw a DictionaryError with the message "Invalid character".

`bool IsPrefix(string word)`

This method returns true if a path down the branches exists for a word. This method will have an implementation very similar to the AddWord method for traveling down the tree. It should return false if it runs into a NULL. If it manages to get through the entire loop without hitting a NULL, it should return true.

While processing the characters, if you encounter a character that is not between 'a' and 'z', you should throw a DictionaryError with the message "Invalid character".

`bool IsWord(string word)`

This method is very similar to the AddWord and IsPrefix method. If you have already implemented the IsPrefix method, then it should be fairly trivial to implement isWord. The main difference is you should return the isWord flag found of the node found at the end of the path.

While processing the characters, if you encounter a character that is not between 'a' and 'z', you should throw a DictionaryError with the message "Invalid character".

IMPORTANT: The IsWord function checks to see if a path exists and returns the isWord at the end of the path.

IsPrefix versus IsWord

IsPrefix checks to see if at least one word in the dictionary starts with a particular prefix. IsWord checks to see if a provided word exists in the dictionary. A word will always be a prefix. However, a prefix will not always be a word.

IMPORTANT: A word is also prefix.

Figuring out the index of a character

You will find it very useful to be able to figure out what index corresponds to a specific letter.

0 1 2 3 4 5 6 ... 25
a b c d e f g ... z

We can take advantage of the fact that characters can easily be cast into integers and use the following to figure out the index of a particular letter.

For example, the following could be used to figure out the index of the character e:

(int)'e' – (int)'a'

The above would evaluate to the integer 4.

It is also easy to find the letter corresponding to an index using the same strategy. For example, if you wanted to find the letter corresponding to 5 (the letter 'f'), you can calculate:

(char) (5 + (int)'a')

Notice we cast the result as a character at the end (you may use any method you like for casting).

Part B: Boggle Solver

Once you have completed and tested your Dictionary class, your next task is creating the Boggle solver.

IMPORTANT: It is strongly recommended you use the Basic_Boggle_Test first to develop your Boggle program. After you are confident that your program is working properly, then you check your program using the other Boggle tests.

`Basic_Boggle_Solver.cpp`

The Basic_Boggle_Solver has some testing framework for you to use to help develop and debug the Boggle class. A hard-coded board is provided as well as a function to get input from the user.

NOTE: Basic_Boggle_Solver is not a Catch test application . It will appear as a CMake application, not a Catch application.

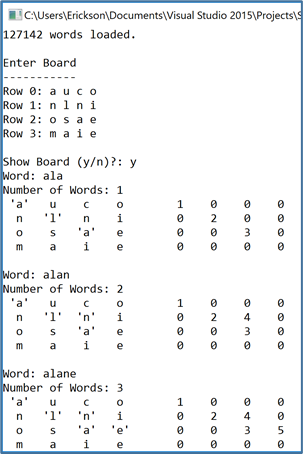
Here is a sample interaction using input from the user:

When solving the board, you have the option of printing out the board or not:

Show the board	Not showing the board

`Boggle()`

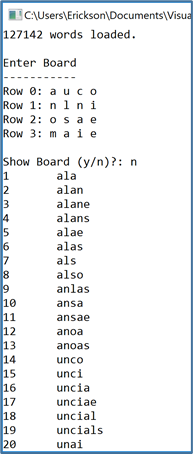The default constructor should initialize the dict with words from dictionary.txt. It initialize each entry of board to the empty string. It should also initialize each entry of visited to false.

`Boggle(filename)`

This constructor should initialize the dict with words from filename. You should use AddWord or LoadDictionaryFile to help you do this. It should also initialize each entry of board to the empty string. It should also initialize each entry of visited to false.

`SetBoard(string board[BOARD_SIZE][BOARD_SIZE])`

This function should copy each entry of board to this->board.

WARNING: Do not just set this->board = board. This results in a shallow copy.

`PrintBoard(ostream& output)`

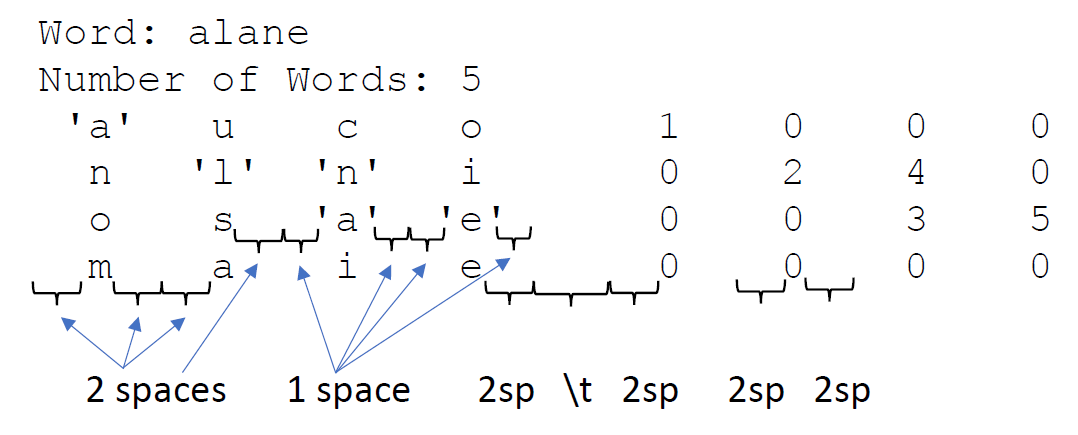
One of the requirements of the program is that the solver should also show the path of the solution. For the example below, we can see how "alane" is found using the grid on the right.

The PrintBoard function should print out the in the same format as the above output. This function should be used by the SolveBoardHelper.

Use the visited matrix to figure out when to print the quotes around the letter. You should print a quote if the visited matrix is not 0 at a given position.

HINT:
It may be helpful to print each letter with two spaces in the front and two spaces in the back:

" m " (two spaces in front, two spaces at back)

If the letter has a quote, then it should print a single space in the front and back:

" 'm' " (one space in front, one space at the back)

You can always look in the test_data at a solve_output_print_#.txt file to see the formatting.

`void SolveBoard(bool printBoard, ostream& output)`

This method finds all the words on the current board stored by board and saves these words to the wordsFound dictionary. The function also outputs the values to the output ostream object. This ostream can be called with cout or an ofstream object (see provided code in Boggle_Solver.cpp). The SolveBoard method serves mainly as a wrapper function for the SolveBoardHelper method. This function should reset the wordsFound dictionary each time it is run.

`void SaveSolve(filename)`

This should use the SaveDictionaryFile for the wordsFound.

Recursion Strategy

A straightforward strategy to finding all the words on the board is to use recursive backtracking. The general idea is to start at each position and then explore all paths originating at that position being careful not to re-visit grid positions.

The solution will start with the SolveBoard function. SolveBoard will serve as a "wrapper" for another SolveBoardHelper function that will do the heavy lifting of the recursion:

For each position on the board
    Find all of the words on the board starting at this position

In terms of the algorithm, this will be writen as:

For each position on the board
	Call SolveBoardHelper starting at the current board position

The job of SolveBoardHelper is to recursively check the surrounding 8 positions.

I suggest thinking about the base case(s) first. Be sure to make use of the isPrefix method to prevent exploration of paths that will not produce words.

NOTE: A solution using this strategy is very short (solutions are about 40 lines or less). If you find yourself writing lot of code, you may want to rethink your strategy.

Each call to SolveBoardHelper function will require multiple variables in order to complete its task:

What row and col to start
What the current step is (see previous diagram for Board Printing)
A string that stores the current prefix/path on the board
A way to remember all the previously visited spaces
A way to remember words you have already found
The ostream object to output results

I strongly suggest you use a debugger or use a generous number of cout statements to help you debug.

To get the same output order as the provided test output, you should search in the following order:

North
Northeast
East
Southeast
South
Southwest
West
Northwest

HINT: Be sure to review the maze example that go over in class.
This example provides a strategy that is very close to what you need for this function.

joqim/Boggle-Solver

Warning

Deliverables

Questions (3 pts/question)

Recommended Implementation Order

Dictionary Class (Part A)

Boggle Class (Part B)

Boggle Solver

Part A: Dictionary

Prefix

Basic_Dictionary.cpp

struct Node

Dictionary() Default Constructor

Dictionary(const Dictionary& otherDict)

Dictionary& operator=(const Dictionary& otherDict)

copyOther(const Dictionary& otherDict)

void MakeEmpty()

Dictionary(string filename)

void LoadDictionaryFile(string filename)

void SaveDictionaryFile(string filename)

void AddWord(string word)

bool IsPrefix(string word)

bool IsWord(string word)

IsPrefix versus IsWord

Figuring out the index of a character

Part B: Boggle Solver

Basic_Boggle_Solver.cpp

Boggle()

Boggle(filename)

SetBoard(string board[BOARD_SIZE][BOARD_SIZE])

PrintBoard(ostream& output)

void SolveBoard(bool printBoard, ostream& output)

void SaveSolve(filename)

Recursion Strategy

`Basic_Dictionary.cpp`

`struct Node`

`Dictionary() Default Constructor`

`Dictionary(const Dictionary& otherDict)`

`Dictionary& operator=(const Dictionary& otherDict)`

`copyOther(const Dictionary& otherDict)`

`void MakeEmpty()`

`Dictionary(string filename)`

`void LoadDictionaryFile(string filename)`

`void SaveDictionaryFile(string filename)`

`void AddWord(string word)`

`bool IsPrefix(string word)`

`bool IsWord(string word)`

`Basic_Boggle_Solver.cpp`

`Boggle()`

`Boggle(filename)`

`SetBoard(string board[BOARD_SIZE][BOARD_SIZE])`

`PrintBoard(ostream& output)`

`void SolveBoard(bool printBoard, ostream& output)`

`void SaveSolve(filename)`