Sequential and parallel fast Fourier transform algorithms for image compression.
A fast Fourier transform algorithm quickly computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies.
This project focuses on the application of fast Fourier transforms for image compression. A Fourier transform allows deconstructs an image to its frequncy domain. In this domain, one can remove insignificant frequncies, essentially stripping data from the image. One can then reconstruct the image with less frequncies to obtain a "compressed" image. For the sake of simplicity, image width and height are constrained to be a power of two and all images are greyscaled before fourier transform computations.
In this project, four types algorithms were implemented and their execution times were analyzed based on the number of threads:
- Serial 2D FFT w/ Serial 1D FFT
- Parallel 2D FFT w/ Serial 1D FFT
- Serial 2D FFT w/ Parallel 1D FFT
- Parallel 2D FFT w/ Parallel 1D FFT
Note: The program does not actually output a compressed jpeg image. It only shows what a compressed image would look like since the ouput is always simply written to a png.
| Input | 10% | 2% | 1% |
|---|---|---|---|
 |
 |
 |
 |
Notice the loss of detail, particularly in the girl's eyebrows, and the man's earring disapearing at higher rates of compression.
| Input | 10% | 5% | 1% |
|---|---|---|---|
 |
 |
 |
 |
Compression at lower rates removes some noise from this image (which is a render from my ray tracer). However, compression at higher rates adds more noise.
| Input | 1% | 0.2% | 0.1% |
|---|---|---|---|
 |
 |
 |
 |
Notice the loss of detail, particularly in the hair.
All algorithms modify the data in-place.
This is the standard Cooley-Tukey Radix-2 decimination-in-frequncy algorithm. This is a divide-and-conquer algorithm that recursively divides the transform into two pieces of size N/2 at each step, and is therefore limited to power-of-two sizes.
This is an optimized Cooley-Tukey FFT decimation-in-time algorithm that uses bit-reversal and a table for the exponentiation. Unfortunatly, the parallelization of my implementation here is quite limited and only involves breaking down loops over data into blocks for each thread.
This is the standard sequantial 2D FFT that invloves perfoming a 1D FFT on each row of the image data matrix and then on each column of the resuling matrix.
This is a 2D FFT that makes each thread perform a 1D FFT on each row of a block of rows of the image data matrix. Then, after syncronization, each thread performs a 1D FFT on each column of a of the resulting matrix. When used with the parallel 1D FFT, the 1D FFT computations only use 2 threads. For example, if the this algorithm is used with 8 threads, the 2D computations are only done using 4 threads and since each 2D computation thread requires doing 1D computation, each of the 4 threads will only spawn 2 threads, making the total number of threads to be 8.
After a fourier transform is done, the frequncies are sorted and only a certain fraction of frequncies are kept, the rest of the data in the matrix is set to 0. Finding exactly which data to keep is the often very slow with large data matrices. I'm aware that such precision is usually not neccesary and a randoming sampling to approximated the distribution of the frequncies and then choosing a cut-off would have been much more faster than finding the exact cut-off.
$ g++ -O3 main.cpp -D_GLIBCXX_PARALLEL -fopenmp -ltbb -std=c++17 -o main.out
$ ./main.out <image filename> <fraction of data to keep>
The output images are stored as output1.png, output2.png, output3.png, and output4.png. All outputs are essentially the same apart from minuscule differences caused by numerial precision differences of the fast Fourier transform algorithms.
$ ./main.out images/philip.png 0.05 # keeps only 5% of the data in philip.png
Analysis of excution time was only performed for the largest image (images/philip.png 2048x2048). All tests were run on a machine with an eight core processor. Execution time is not the complete program execution time but only the execution time of the fourier transform function and its inverse.
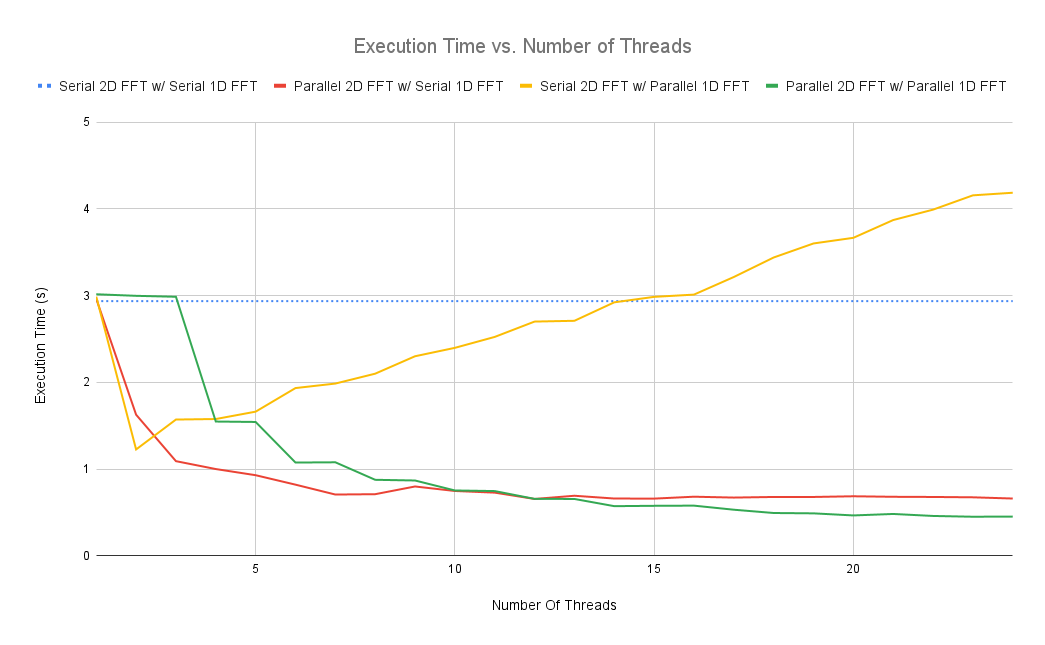
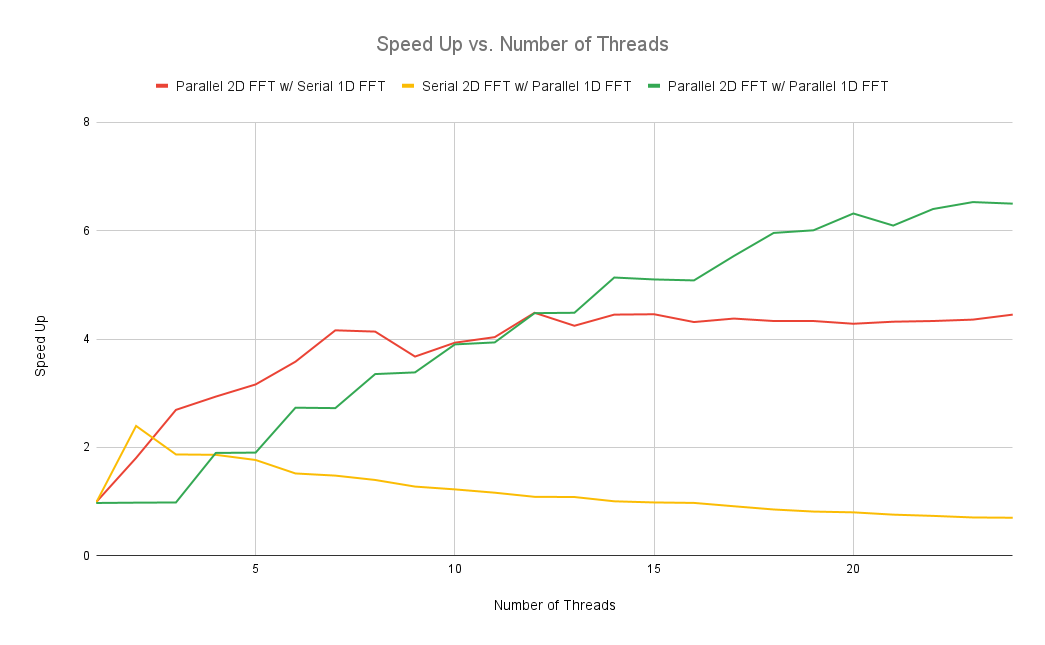
The fully sequential algorithm (Serial 2D FFT w/ Serial 1D FFT) is independant of the number of threads as expected. The fully parallel algorithm (Parallel 2D FFT w/ Parallel 1D FFT) offers the best speed-up with a high number of threads. However, parallelizing only the 2D FFT (Parallel 2D FFT w/ Serial 1D) seems to offer a better speed-up when the number of threads is below 12. The worst algorithm involves parallelizing only the 1D FFT (Serial 2D FFT w/ Parallel 1D FFT). It does not offer as significant of a speed-up when the number of threads is over 3. In fact, it seems to progressivly get worse when the number of threads is increased. This might be due to thread-spawning overhead becoming significant or I just have a bug in my code 😕 .
The overall image compression of all the algorithms implemented is successful. We observe that more information is lost when we increase the compression rate. The best algorithm is the fully parallel implementation (Parallel 2D FFT w/ Parallel 1D FFT) as it offers the best speed-up with a higher number of threads. The worst algorithm seems to be the one which parallelizes only the 1D FFT (Serial 2D FFT w/ Parallel 1D FFT) since the speed-up seems to decrease when the number of threads is high.