Molecular Swarm Optimization (MSO)

Implementation of the method proposed in the paper "Efficient Multi-Objective Molecular Optimization in a Continuous Latent Space" by Robin Winter, Floriane Montanari, Andreas Steffen, Hans Briem, Frank Noé and Djork-Arné Clevert.¹

Dependencies

cddd

Installing

cd mso
pip install .

Getting Started

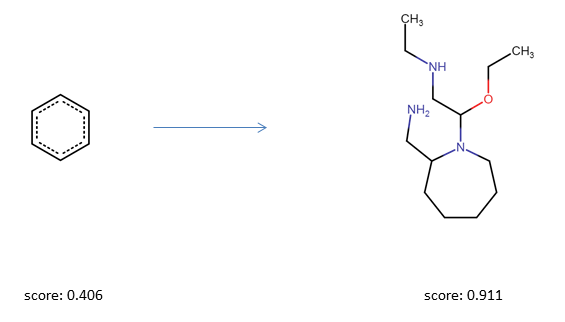
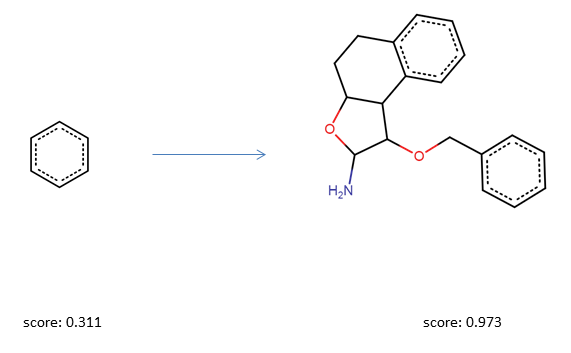
As a first simple experiment, we will optimize a query molecule with respect to the drug likeness score (QED Bickerton et al.). We will start the optimization from a simple benzene molecule which has a QED score of 0.31.

from mso.optimizer import BasePSOptimizer
from mso.objectives.scoring import ScoringFunction
from mso.objectives.mol_functions import qed_score
from cddd.inference import InferenceModel
infer_model = InferenceModel() # The CDDD inference model used to encode/decode molecular SMILES strings to/from the CDDD space. You might need to specify the path to the pretrained model (e.g. default_model)
init_smiles = "c1ccccc1" # SMILES representation of benzene
scoring_functions = [ScoringFunction(func=qed_score, name="qed", is_mol_func=True)] # wrap the drug likeness score inside a scoring function instance

After loading some packages and defining the inference model, starting point and objective function, we can create an instance of the Particle Swarm Optimizer. Here we only utilize one swarm with 100 particles.

opt = BasePSOptimizer.from_query(
    init_smiles=init_smiles,
    num_part=200,
    num_swarms=1,
    inference_model=infer_model,
    scoring_functions=scoring_functions)

Now we can run the optimization just for a few steps.

opt.run(20)

The best results are summarized in opt.best_solutions. The optimization history (best solution at each step in each swarm) is summarized in opt.best_fitness_history. Most of the time, the optimizer should be able to find a solution with a score higher than 0.8 already after a few steps.

Desirability Scaling

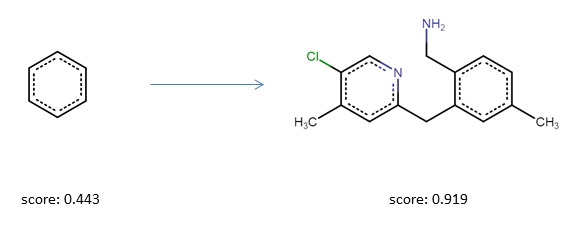
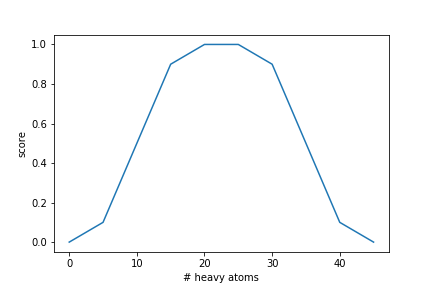
Often, the goal is not to maximize a function as much as possible but to keep a molecular property within a certain range. To account for this, the ScoringFunction class can rescale the output of an objective function with respect to a desirability curve. To demonstrate this functionality, here we optimize the number of heavy atoms in a molecule. We would like to generate molecules that have a certain number (or range) of heavy atoms. In this case, generated molecules should have between 20 and 25 heavy atoms. To achieve this, we define a desirability curve that has its peak in this range and assigns lower scores below and above:

from mso.objectives.mol_functions import heavy_atom_count
hac_desirability = [{"x": 0, "y": 0}, {"x": 5, "y": 0.1}, {"x": 15, "y": 0.9}, {"x": 20, "y": 1.0}, {"x": 25, "y": 1.0}, {"x": 30, "y": 0.9,}, {"x": 40, "y": 0.1}, {"x": 45, "y": 0.0}]
scoring_functions = [ScoringFunction(heavy_atom_count, "hac", desirability=hac_desirability, is_mol_func=True)]

The resulting curve looks like this:

And indeed, running the optimizer for a few steps results in a molecules with the optimal amound of heavy atoms.

Multi-Objective Optimization

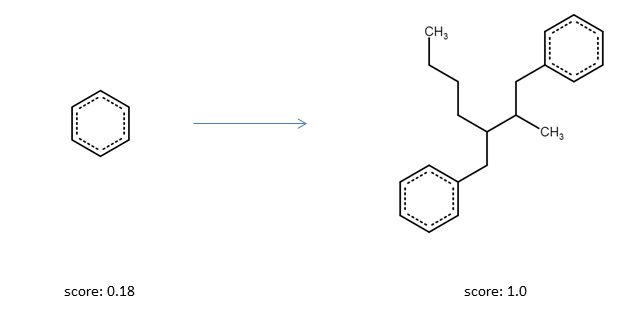
To optimize multiple objective functions at the same time, they can be append to the same list.

scoring_functions = [ScoringFunction(heavy_atom_count, "hac", desirability=hac_desirability, is_mol_func=True), ScoringFunction(qed_score, "qed", is_mol_func=True)]

Optionally, an individual weight can be assigned to each scoring function to balance their importance.

Constrained Optimization

Sometimes it might be of interest to constrain the chemical space to a certain region during the optimization. This can be done, for example, by applying a substructure constrain. In this example optimize again for QED and a defined range of heavy atoms but penalize for solutions that have a benzene substructure. Moreover, to avoid generating large macrocycles we also penalize for them. The necesarry functions are included in the mol_functions module:

from mso.objectives.mol_functions import substructure_match_score, penalize_macrocycles
from functools import partial
substructure_match_score = partial(substructure_match_score, query=Chem.MolFromSmiles("c1ccccc1")) # use partial to define the additional argument (the substructure) 
miss_match_desirability = [{"x": 0, "y": 1}, {"x": 1, "y": 0}] # invert the resulting score to penalize for a match.
scoring_functions = [
    ScoringFunction(heavy_atom_count, "hac", desirability=hac_desirability, is_mol_func=True),
    ScoringFunction(qed_score, "qed", is_mol_func=True),
    ScoringFunction(substructure_match_score, "miss_match",desirability=miss_match_desirability, is_mol_func=True),
    ScoringFunction(penalize_macrocycles, "macro", is_mol_func=True)
]

Writing your own Scoring Function

The ScoringFunction class can wrap any function that has following properties:

Takes a RDKit mol object as input and returns a number as score.
Takes the CDDD positions of the particles in a swarm as input [num_particels, num_dim] and returns an array of scores [num_particels].

For examples, see the modules mso.objectives.mol_functions and mso.objectives.emb_functions.

References

[1] Chemical Science, 2019, DOI: 10.1039/C9SC01928F https://pubs.rsc.org/en/content/articlelanding/2019/SC/C9SC01928F#!divAbstract

jrwnter/mso