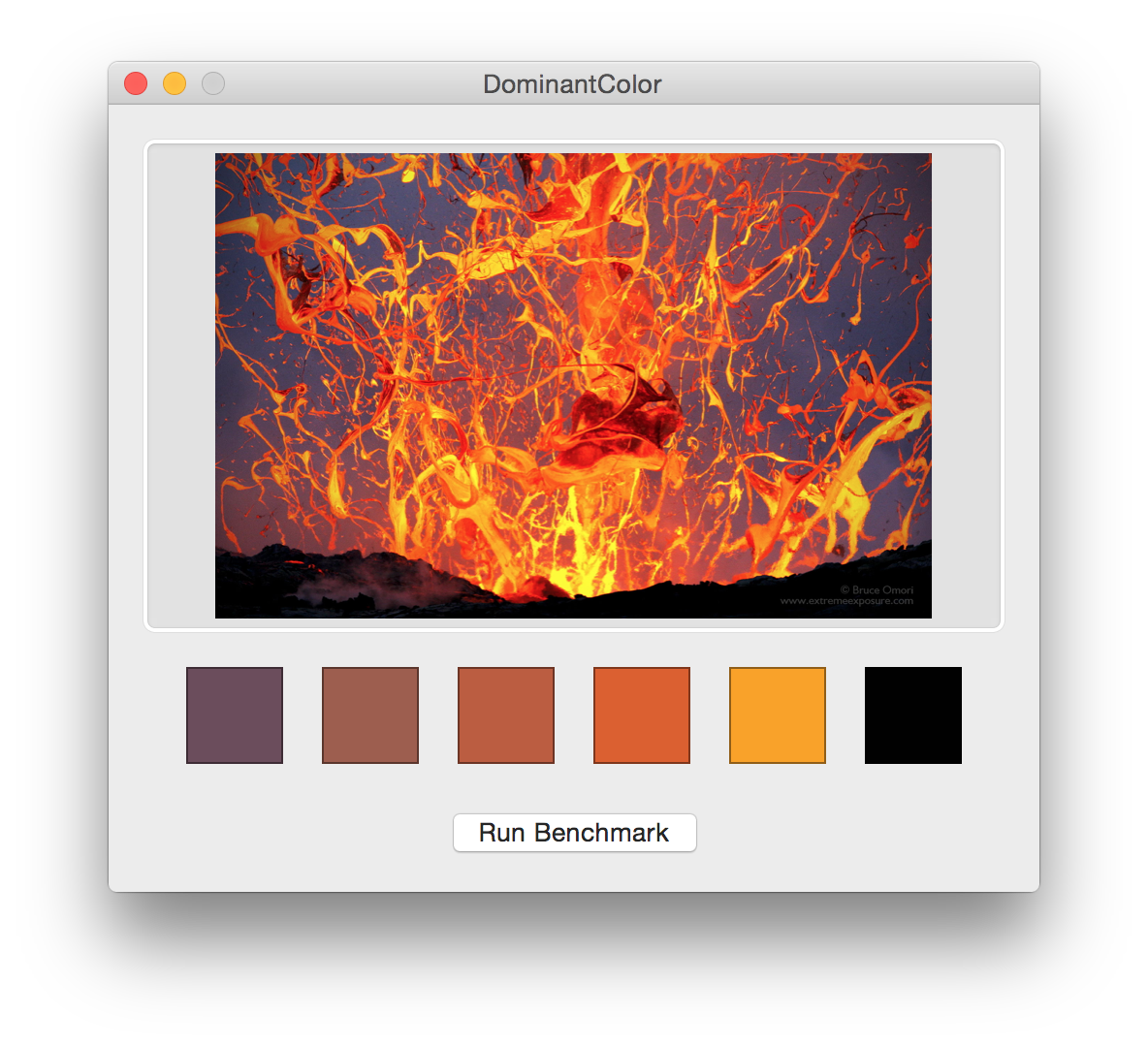
Finding the dominant colors of an image using the CIE LAB color space and the k-means clustering algorithm.
The RGB color space does not take human perception into account, so the CIELAB color space is used instead, which is designed to approximate human vision [1].
The conversion from RGB values to LAB values requires first transforming the RGB values to an absolute color space like sRGB[2]. On iOS, this conversion is not necessary because sRGB is the native device color space[3]. On OS X, the conversion can be performed using -[NSColorSpace sRGBColorSpace].
Once the colors have been converted to sRGB, they are first converted to linear sRGB values and then to CIE XYZ values[4]. Finally, they are converted to the CIE LAB color space[5] using a D65 standard illuminant[6][7].
A color difference algorithm is used to group similar colors. API consumers can choose between the CIE 76[8], CIE 94[9], and CIE 2000[10] algorithms for low, medium, and high color grouping accuracy, respectively. The default algorithm is CIE 94, as it provides results that are close to CIE 2000 with a negligible performance impact in comparison to CIE 76.
Pixels are grouped into clusters of dominant colors using a standard k-means clustering algorithm[11][12][13].
The k-value was originally chosen based on the rule of thumb k = sqrt(n/2)[14] but this resulted in k-values that were too large to run in a reasonable amount of time for large values of n. Right now, I'm using a magic value of 16 because empirical testing showed that it yielded the best results for many different images but I'm still looking into a number of more data-driven alternate approaches.
The initial centroids are currently selected on a random basis. An alternative approach is to use the k-means++ algorithm, in which after the first centroid is selected randomly, the subsequent centroids are selected with probability proportional to the distance from the randomly selected centroid.
The k-means algorithm has a worst case runtime that is super-polynomial in the input size[15], so sampling large numbers of pixels is a problem. Images are automatically downsampled such that the total number of pixels is less than or equal to a specified maximum number of pixels to sample. The value I've been using is 1000, which is a good balance between accurate results and runtime.
Everything is implemented in Swift except for the functions that convert between color spaces, which use GLKit and thus must be written in C (since Swift doesn't support C unions at this time).
The project includes Mac and iOS apps that can be used to see the results of the algorithm and to run a simple benchmark.
- Indragie Karunaratne
- @indragie
- http://indragie.com
Licensed under the MIT License.
1 http://en.wikipedia.org/wiki/Lab_color_space#Advantages
2 http://en.wikipedia.org/wiki/Lab_color_space#RGB_and_CMYK_conversions
3 https://developer.apple.com/library/ios/documentation/GraphicsImaging/Reference/CGColorSpace/index.html
4 http://en.wikipedia.org/wiki/SRGB#The_forward_transformation_.28CIE_xyY_or_CIE_XYZ_to_sRGB.29
5 http://en.wikipedia.org/wiki/Lab_color_space#CIELAB-CIEXYZ_conversions
6 http://en.wikipedia.org/wiki/Illuminant_D65
7 http://www.easyrgb.com/index.php?X=MATH&H=15#text15
8 http://en.wikipedia.org/wiki/Color_difference#CIE76
9 http://en.wikipedia.org/wiki/Color_difference#CIEDE2000
10 http://en.wikipedia.org/wiki/Color_difference#CIEDE2000
11 http://en.wikipedia.org/wiki/K-means_clustering
12 http://users.eecs.northwestern.edu/~wkliao/Kmeans/
13 http://cs.smu.ca/~r_zhang/code/kmeans.c
14 http://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set#cite_note-1
15 http://en.wikipedia.org/wiki/K-means%2B%2B