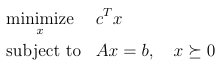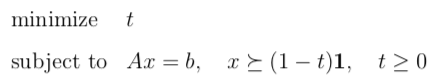This repo implements a simple standard form Linear Programming (LP) solver in Python.
The solver uses the barrier method which involves solving an LP centering problem in every iteration (see Chapter 11 of Boyd and Vandenberghe's Convex Optimization textbook).
lp_solver.pyimplements theLPSolverclass, which can be used as follows:
# Randomly generate a feasible LP problem
m, n = 100, 500
A = np.random.randn(m, n)
A[0,:] = np.random.rand(n) + 0.1 # make sure problem is bounded
b = np.dot(A, np.random.rand(n) + 0.01)
c = np.random.rand(n)
# Solve the problem
solver = LPSolver(mu=10, tol=1e-4)
solver.solve(A, b, c)
assert solver.status == 'optimal'
print("optimal value: {}".format(solver.value))test.pyverifies LPSolver's basic functionalities by running it on both feasible and infeasible LP problems. The results are verified against the output from CVXPY.
The feasible start barrier method can be summarized as follows:
The centering problem is an equality constrained optimization problem that can be solved using Newton's method with backtracking line search (see LPCenteringSolver in lp_solver.py)
Strict feasibility can be first determined by solving the following LP problem, of which a feasible starting point can be easily identified:
The original LP is strictly feasible if and only if the optimal value of this problem is less than 1. The optimal x obtained from this problem can be used as the starting point for the barrier method.