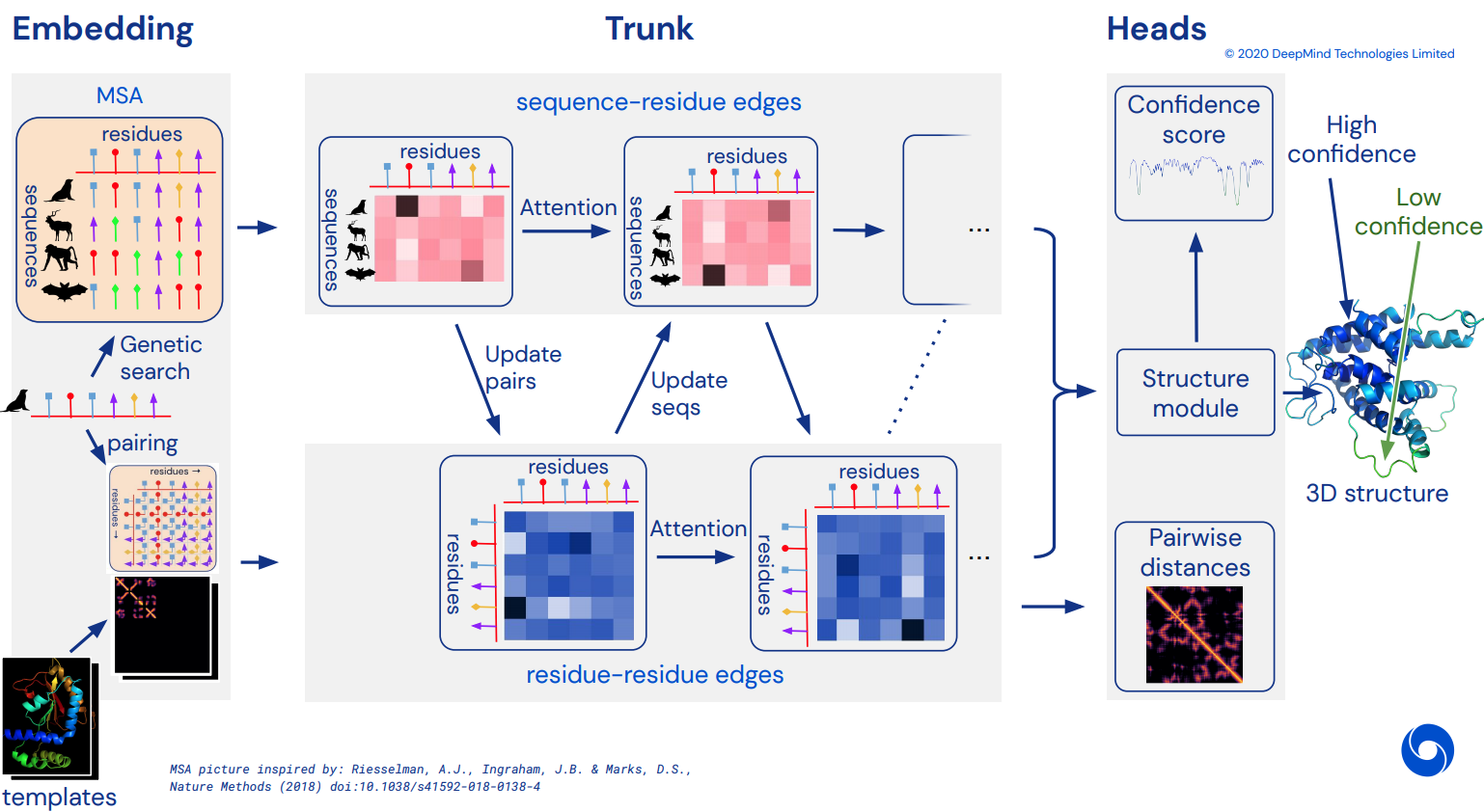
To eventually become an unofficial working Pytorch implementation of Alphafold2, the breathtaking attention network that solved CASP14. Will be gradually implemented as more details of the architecture is released.
Once this is replicated, I intend to fold all available amino acid sequences out there in-silico and release it as an academic torrent, to further science. If you are interested in replication efforts, please drop by #alphafold at this Discord channel
$ pip install alphafold2-pytorchPredicting distogram, like Alphafold-1, but with attention
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2(
dim = 256,
depth = 2,
heads = 8,
dim_head = 64,
reversible = False # set this to True for fully reversible self / cross attention for the trunk
).cuda()
seq = torch.randint(0, 21, (1, 128)).cuda() # AA length of 128
msa = torch.randint(0, 21, (1, 5, 120)).cuda() # MSA doesn't have to be the same length as primary sequence
mask = torch.ones_like(seq).bool().cuda()
msa_mask = torch.ones_like(msa).bool().cuda()
distogram = model(
seq,
msa,
mask = mask,
msa_mask = msa_mask
) # (1, 128, 128, 37)You can also turn on prediction for the angles, by passing a predict_angles = True on init. The below example would be equivalent to trRosetta but with self / cross attention.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2(
dim = 256,
depth = 2,
heads = 8,
dim_head = 64,
predict_angles = True # set this to True
).cuda()
seq = torch.randint(0, 21, (1, 128)).cuda()
msa = torch.randint(0, 21, (1, 5, 120)).cuda()
mask = torch.ones_like(seq).bool().cuda()
msa_mask = torch.ones_like(msa).bool().cuda()
distogram, theta, phi, omega = model(
seq,
msa,
mask = mask,
msa_mask = msa_mask
)
# distogram - (1, 128, 128, 37),
# theta - (1, 128, 128, 25),
# phi - (1, 128, 128, 13),
# omega - (1, 128, 128, 25)Fabian's recent paper suggests iteratively feeding the coordinates back into SE3 Transformer, weight shared, may work. I have decided to execute based on this idea, even though it is still up in the air how it actually works.
You can also use E(n)-Transformer for the refinement, if you are in the experimental mood (paper just came out a week ago).
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2(
dim = 256,
depth = 2,
heads = 8,
dim_head = 64,
predict_coords = True,
use_se3_transformer = True, # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
num_backbone_atoms = 3, # C, Ca, N coordinates
structure_module_dim = 4, # se3 transformer dimension
structure_module_depth = 1, # depth
structure_module_heads = 1, # heads
structure_module_dim_head = 16, # dimension of heads
structure_module_refinement_iters = 2 # number of equivariant coordinate refinement iterations
).cuda()
seq = torch.randint(0, 21, (2, 64)).cuda()
msa = torch.randint(0, 21, (2, 5, 60)).cuda()
mask = torch.ones_like(seq).bool().cuda()
msa_mask = torch.ones_like(msa).bool().cuda()
coords = model(
seq,
msa,
mask = mask,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residueA paper by Jinbo Xu suggests that one doesn't need to bin the distances, and can instead predict the mean and standard deviation directly. You can use this by turning on one flag predict_real_value_distances, in which case, the distance prediction returned will have a dimension of 2 for the mean and standard deviation respectively.
If predict_coords is also turned on, then the MDS will accept the mean and standard deviation predictions directly without having to calculate that from the distogram bins.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2(
dim = 256,
depth = 2,
heads = 8,
dim_head = 64,
predict_coords = True,
predict_real_value_distances = True, # set this to True
use_se3_transformer = True,
num_backbone_atoms = 3,
structure_module_dim = 4,
structure_module_depth = 1,
structure_module_heads = 1,
structure_module_dim_head = 16,
structure_module_refinement_iters = 2
).cuda()
seq = torch.randint(0, 21, (2, 64)).cuda()
msa = torch.randint(0, 21, (2, 5, 60)).cuda()
mask = torch.ones_like(seq).bool().cuda()
msa_mask = torch.ones_like(msa).bool().cuda()
coords = model(
seq,
msa,
mask = mask,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residueYou can train with Microsoft Deepspeed's Sparse Attention, but you will have to endure the installation process. It is two-steps.
First, you need to install Deepspeed with Sparse Attention
$ sh install_deepspeed.shNext, you need to install the pip package triton
$ pip install tritonIf both of the above succeeded, now you can train with Sparse Attention!
Sadly, the sparse attention is only supported for self attention, and not cross attention. I will bring in a different solution for making cross attention performant.
model = Alphafold2(
dim = 256,
depth = 12,
heads = 8,
dim_head = 64,
max_seq_len = 2048, # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
sparse_self_attn = (True, False) * 6 # interleave sparse and full attention for all 12 layers
).cuda()To save on memory for cross attention, you can set a compression ratio for the key / values, following the scheme laid out in this paper. A compression ratio of 2-4 is usually acceptable.
model = Alphafold2(
dim = 256,
depth = 12,
heads = 8,
dim_head = 64,
cross_attn_compress_ratio = 3
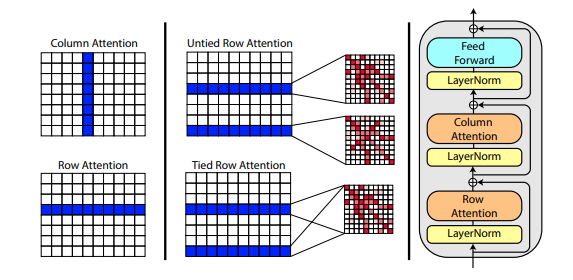
).cuda()A new paper by Roshan Rao proposes using axial attention for pretraining on MSA's. Given the strong results, this repository will use the same scheme in the trunk, specifically for the MSA self-attention.
You can also tie the row attentions of the MSA with the msa_tie_row_attn = True setting on initialization of Alphafold2. However, in order to use this, you must make sure that none of the rows in the batch of MSA is made of padding. In other words, your msa_mask must be completely set to True
model = Alphafold2(
dim = 256,
depth = 2,
heads = 8,
dim_head = 64,
msa_tie_row_attn = True # just set this to true, but batches of MSA must not contain any row that is all padding
)Template processing is also largely done with axial attention, with cross attention done along the number of templates dimension. This largely follows the same scheme as in the recent all-attention approach to video classification as shown here.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2(
dim = 256,
depth = 5,
heads = 8,
dim_head = 64,
reversible = True,
sparse_self_attn = False,
max_seq_len = 256,
cross_attn_compress_ratio = 3
).cuda()
seq = torch.randint(0, 21, (1, 16)).cuda()
mask = torch.ones_like(seq).bool().cuda()
msa = torch.randint(0, 21, (1, 10, 16)).cuda()
msa_mask = torch.ones_like(msa).bool().cuda()
templates_seq = torch.randint(0, 21, (1, 2, 16)).cuda()
templates_coors = torch.randint(0, 37, (1, 2, 16, 3)).cuda()
templates_mask = torch.ones_like(templates_seq).bool().cuda()
distogram = model(
seq,
msa,
mask = mask,
msa_mask = msa_mask,
templates_seq = templates_seq,
templates_coors = templates_coors,
templates_mask = templates_mask
)If sidechain information is also present, in the form of the unit vector between the C and C-alpha coordinates of each residue, you can also pass it in as follows.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2(
dim = 256,
depth = 5,
heads = 8,
dim_head = 64,
reversible = True,
sparse_self_attn = False,
max_seq_len = 256,
cross_attn_compress_ratio = 3
).cuda()
seq = torch.randint(0, 21, (1, 16)).cuda()
mask = torch.ones_like(seq).bool().cuda()
msa = torch.randint(0, 21, (1, 10, 16)).cuda()
msa_mask = torch.ones_like(msa).bool().cuda()
templates_seq = torch.randint(0, 21, (1, 2, 16)).cuda()
templates_coors = torch.randn(1, 2, 16, 3).cuda()
templates_mask = torch.ones_like(templates_seq).bool().cuda()
templates_sidechains = torch.randn(1, 2, 16, 3).cuda() # unit vectors of difference of C and C-alpha coordinates
distogram = model(
seq,
msa,
mask = mask,
msa_mask = msa_mask,
templates_seq = templates_seq,
templates_mask = templates_mask,
templates_coors = templates_coors,
templates_sidechains = templates_sidechains
)There are two equivariant self attention libraries that I have prepared for the purposes of replication. One is the implementation by Fabian Fuchs as detailed in a speculatory blogpost. The other is from a recent paper from Deepmind, claiming their approach is better than using irreducible representations.
A new paper from Welling uses invariant features for E(n) equivariance, reaching SOTA and outperforming SE3 Transformer at a number of benchmarks, while being much faster. You can use this by simply setting use_se3_transformer = False on Alphafold2 initialization.
$ python setup.py testThis library will use the awesome work by Jonathan King at this repository. Thank you Jonathan 🙏!
We also have the MSA data, all ~3.5 TB worth, downloaded and hosted by Archivist, who owns The-Eye project. (They also host the data and models for Eleuther AI) Please consider a donation if you find them helpful.
$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txthttps://xukui.cn/alphafold2.html
https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf
https://pubmed.ncbi.nlm.nih.gov/33637700/
tFold presentation, from Tencent AI labs
- Final step - Fast Relax - Installation Instructions:
- Download the pyrosetta wheel from: http://www.pyrosetta.org/dow (select appropiate version) - beware the file is heavy (approx 1.2 Gb)
- Ask for username and password to
@hypnopumpin the Discord
- Ask for username and password to
- Bash >
cd downloads_folder>pip install pyrosetta_wheel_filename.whl
- Download the pyrosetta wheel from: http://www.pyrosetta.org/dow (select appropiate version) - beware the file is heavy (approx 1.2 Gb)
@misc{unpublished2021alphafold2,
title = {Alphafold2},
author = {John Jumper},
year = {2020},
archivePrefix = {arXiv},
primaryClass = {q-bio.BM}
}@article{Rao2021.02.12.430858,
author = {Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander},
title = {MSA Transformer},
year = {2021},
publisher = {Cold Spring Harbor Laboratory},
URL = {https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858},
journal = {bioRxiv}
}@misc{king2020sidechainnet,
title = {SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning},
author = {Jonathan E. King and David Ryan Koes},
year = {2020},
eprint = {2010.08162},
archivePrefix = {arXiv},
primaryClass = {q-bio.BM}
}@misc{alquraishi2019proteinnet,
title = {ProteinNet: a standardized data set for machine learning of protein structure},
author = {Mohammed AlQuraishi},
year = {2019},
eprint = {1902.00249},
archivePrefix = {arXiv},
primaryClass = {q-bio.BM}
}@misc{gomez2017reversible,
title = {The Reversible Residual Network: Backpropagation Without Storing Activations},
author = {Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse},
year = {2017},
eprint = {1707.04585},
archivePrefix = {arXiv},
primaryClass = {cs.CV}
}@misc{fuchs2021iterative,
title = {Iterative SE(3)-Transformers},
author = {Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner},
year = {2021},
eprint = {2102.13419},
archivePrefix = {arXiv},
primaryClass = {cs.LG}
}@misc{satorras2021en,
title = {E(n) Equivariant Graph Neural Networks},
author = {Victor Garcia Satorras and Emiel Hoogeboom and Max Welling},
year = {2021},
eprint = {2102.09844},
archivePrefix = {arXiv},
primaryClass = {cs.LG}
}