Corista Take-home Coding Challenge

Fall 2018, Challenger: Ke Wu

contact: kwu2@wpi.edu

Brief introduction

This package is the full solution for the very interesting guessing number problem and include the following parts:

solution sorce code to the problem written in JAVA
visualization and analyze code in python
solution explain and instructions of test, aka, this readme file

The final solution was optimized along 3 iteration of agile development which spans two days.

Generated 1 Million test cases and performed a integrated test over two major version of solutions, one as baseline and one as final optimized version.

Test result analysis and Visualization are attached along this readme file. Total time consumed: 5h, 30m (including composing readme)

Dependency

solution written in java requires only the standard library. make sure you installed java 7 or above library. visualizer of test results requires Python libraries (compatible to both 2.7 and 3.6):

pandas for data preprocessing
numpy for data preprocessing
matplotlib for plotting
seaborn for plotting themes

build & run:

I have two solution versions included, the baseline one: solution.java, and the optimized one: solution2.java. To perform a single run on any version of solution:

$ cd solution/corista/
$ javac solution2.java
$ java solution2

To run test cases:

$ cd solution/corista/
$ javac solution2_test.java
$ java solution2_test

Or you can run with parameters:

$ java solution2_test iteration_number /path/to/output_filename.txt

To run the visualization and analyze Python script:

$ cd solution/corista/
$ python plot_results.py

Or you can run with parameters:

$ python plot_results.py input_file.txt

P.S., each solution file including:

feedback() which provide the goat and chicken number according to the description document provided.
getAns(String guess, String serete) which perform the main loop to find the correct number according to feedback() and return the guessing time.
initial_num() which helps initialize the secrete number and guessing number.

Solution explain

compared to the brute-force approach, which generate 00000 to 99999 and the computation cost is 100,000 times. However, to simplify the problem, we can separate the guessing number as five individual digits to match the five corresponding secrete digits using the given information goat and chicken feedback. the initial pseudo code goes like this:

target_number = []
for i in guess:
    if i match and goat_n > prev_goat_n:
        i is target_digit
        target_number.append()
return target_number

this code will introduce at most 5*10 times computations. And the drawback is obvious, we haven't use the chicken feedback information yet. To optimize it, we need to find out the redundent parts and terminate the loop earlier by using the chicken number:

considering the initial cases, if the initial case doesn't even add the chicken number, or the chicken number are still 0, means the initial 5 digits are all wrong, and we drop all these five digits, this is an extreme case though.
inspired by 1., I came up an idea to maintain the guessing digit's loop list, nobody said that we must loop from 0 to 9, so we can pop out the elements that for sure are not in the other positions of the secrete number according to chicken and goat feedback.
further optimization is using the chicken number to find out the correct permutation along the loops.

Test & Analyze

To test the efficiency of the code, I wrote a customizable test class to run the test as many times you want and export the test results to the file you specified. Detailed instructions was written in the Build & Run section. Here's the test result distribution:

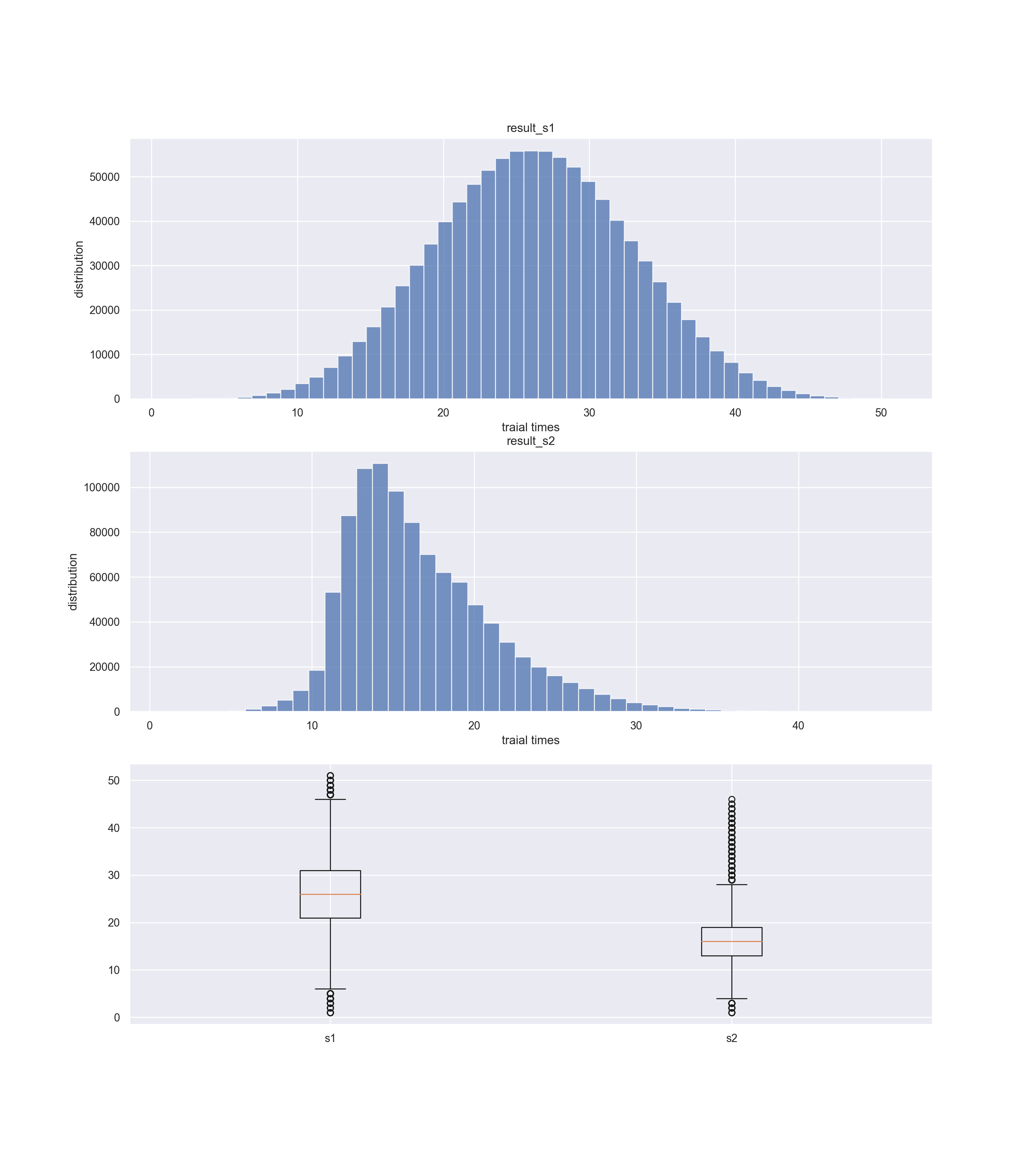
we can see that the baseline, which is the solution, is following a gaussian distribution. this is because we generated our randomized testcase with java.util.Random which perform a gaussian normalization.

it's clear that we have optimized our algorithm at the second version which is around 10 times less than the baseline.

the 3rd plot shows the boxplot of two versions of solutions. It's clear that the second version of algorithm shrinked the distribution along the mean value and the worst case was no bigger than 34 times.

here's some metrics:

 mean s1: 26.176314, mean s2: 16.53913

minor changes related to implementation:

rather than directly generate the numbers from random library (like this: Math.random()*100000) we can randomly choose 5 digits from a 0-9 list and by this way, it's easier to control the permutations.
rather than use the random combination of 5 digis from 0-9, we can choose the random non-repeated digits by doing this, we can leverage the service of chicken condition and terminate the code earlier.
do not allow repeat digits at the initial guess number, to solve the ambiguity of which element credit for chicken number change.

karenwuke/corista_takehome