Linear Time Sinkhorn Divergences using Positive Features
Code of the paper by Meyer Scetbon and Marco Cuturi
Approximation of the Regularized Optimal Transport in Linear Time
In this work, we show that one can approximate the regularized optimal transport in linear time with respect to the number of samples for some usual cost functions, e.g. the square Euclidean distance. We present the time-accuracy tradeoff between different methods to compute the regularized OT when the samples live on the unit sphere.
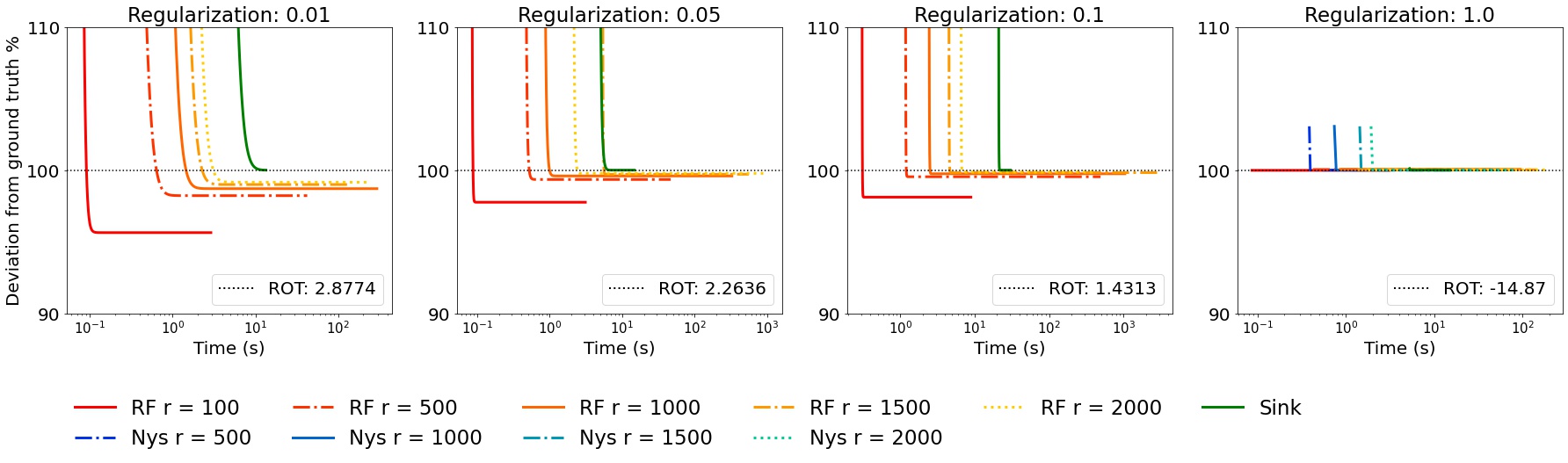
The implementation of the recursive Nystrom is adapted from the MATLAB implementation (https://github.com/cnmusco/recursive-nystrom).
Generative Adversarial Network
We also show that our method offers a constructive way to build a kernel and then a cost function adapted to the problem in order to compare distributions using optimal transport. We show some visual results of the generative models learned using our method on CIFAR10 (left) and CelebA (right).
The implementation of the WGAN is a code adapted from the MMD-GAN implementation (https://github.com/OctoberChang/MMD-GAN).
This repository contains a Python implementation of the algorithms presented in the paper.

