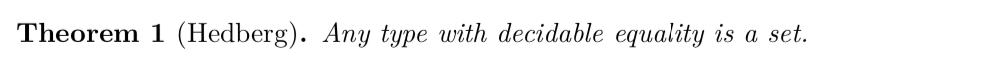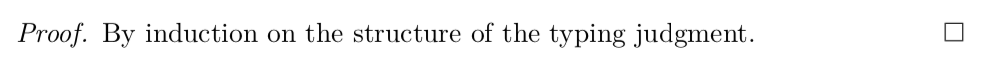A Pandoc filter to convert definition lists into amsthm theorem environments, for compiling to PDF and LaTeX.
The extension supports the following theorem environments:
| Supported environment | Supported Markdown identifiers |
|---|---|
definition |
Definition, Def |
theorem |
Theorem, Thm |
lemma |
Lemma |
proof |
Proof, Pf |
Note that compilation targets other than PDF and LaTeX have not been tested. Notably, this includes HTML.
Given the following Markdown:
Lemma (Pumping Lemma). \label{pumping}
: Let $L$ be a regular language. Then there exists an integer $p \geq 1$ called the "pumping length" which depends only on $L$, such that every string $w \in L$ of length at least $p$ can be divided into three substrings $w = xyz$ such that the following conditions hold:
- $|y| \geq 1$
- $|xy| \leq p$
- $xy^n z \in L$, for all $n \geq 0$.
That is, the non-empty substring $y$ occurring within the first $p$ characters of $w$ can be "pumped" any number of times, and the resulting string is always in $L$.we transform it into this PDF output:

equivalent to this LaTeX:
\begin{lemma}[Pumping Lemma] \label{lem}
Let \(L\) be a regular language. Then there exists an integer
\(p \geq 1\) called the ``pumping length'' which depends only on \(L\),
such that every string \(w \in L\) of length at least \(p\) can be
divided into three substrings \(w = xyz\) such that the following
conditions hold:
\begin{itemize}
\tightlist
\item
\(|y| \geq 1\)
\item
\(|xy| \leq p\)
\item
\(xy^n z \in L\), for all \(n \geq 0\).
\end{itemize}
That is, the non-empty substring \(y\) occurring within the first \(p\)
characters of \(w\) can be ``pumped'' any number of times, and the
resulting string is always in \(L\).
\end{lemma}You must have Pandoc installed and available in your PATH.
You can either download a prebuilt binary from the Releases page, or clone and stack install this repository, which copies the pandoc-theorem-exe binary to your global Stack install location.
Check that pandoc-theorem-exe is in your PATH:
$ which pandoc-theorem-exe
/Users/slim/.local/bin/pandoc-theorem-exe # or a different path
pandoc-theorem repurposes the syntax for definition lists, checking for recognized identifiers.
Theorem (Fermat's Little).
: If $p$ is a prime number, then for any integer $a$, the number $$a^p - a$$ is an integer multiple of $p$.In general, the format looks like this:
<term>
: <body>where <body> is standard Pandoc Markdown (with inline or block formatting), and <term> is one of the following:
<term> ::= <identifier>.
| <identifier> (<name>).
| <identifier> (<name>). <additional text>
That is, a <term> consists of:
- A supported environment identifier (required), followed by either
- A period (
.) if the environment has no name, or - A name in parentheses
()which will be passed to the LaTeX environment
- A period (
- Optional additional Pandoc Markdown (e.g. for LaTeX
\labels)
Supported <identifier> values are documented.
Confused about indentation, line spacing, or the : characters? Consult the documentated syntax for Pandoc definition lists.
More examples can be found in the Examples section below.
To use, pass the pandoc-theorem-exe executable as a filter to Pandoc:
# Compile to PDF.
pandoc --filter pandoc-theorem-exe input.md -H header.tex -o output.pdf
# Output LaTeX.
pandoc --filter pandoc-theorem-exe input.md -H header.tex -t latexNote that you will always need to include the following header file using Pandoc's -H flag:
% examples/header.tex
\usepackage{amsthm}
\newtheorem{definition}{Definition}
\newtheorem{lemma}{Lemma}
\newtheorem{theorem}{Theorem}This repository includes an example Markdown file in examples/kitchen-sink.md. You can explore its output using the following command:
pandoc --filter pandoc-theorem-exe examples/kitchen-sink.md -H examples/header.tex -o examples/kitchen-sink.pdfTheorem (Hedberg).
: Any type with decidable equality is a set.Lemma (Pumping Lemma). \label{lem}
: Let $L$ be a regular language. Then there exists an integer $p \geq 1$ called the "pumping length" which depends only on $L$, such that every string $w \in L$ of length at least $p$ can be divided into three substrings $w = xyz$ such that the following conditions hold:
- $|y| \geq 1$
- $|xy| \leq p$
- $xy^n z \in L$, for all $n \geq 0$.
That is, the non-empty substring $y$ occurring within the first $p$ characters of $w$ can be "pumped" any number of times, and the resulting string is always in $L$.Proof.
: By induction on the structure of the typing judgment.Def (Agda).
: A dependently-typed programming language often used for interactive theorem proving.
: A video game that doesn't mean you understand the underlying theory, according to Bob.If you do not use
Groceries
: Bananas
: Lenses
: Barbed wireProgramming language checklist
: *Strictures:* Does the language have sufficiently many restrictions? It is always easier to relax strictures later on.
: *Affordances:* Actually, these don't really matter.In addition to John MacFarlane's incredible work on Pandoc itself, this filter benefited from the following prior efforts:
- pandoc-moreblock-filter and npfc by Norman Markgraf
- defenv.py by Michael Färber, documented in Pandoc filters for scientific writing and the earlier Theorems in Pandoc