## Item 1 Item 2 Item 3 Item 4 Item 5
## 1 0 0 0 0 0
## 2 0 0 0 0 0
## 3 0 0 0 0 0
## 4 0 0 0 0 1
## 5 0 0 0 0 1
## 6 0 0 0 0 1
The Law School Admission Test (LSAT), The LSAT is a classical example in educational testing for measuring ability traits. This test was designed to measure a single latent ability scale.
Format
A data frame with the responses of 1000 individuals to 5 questions.
References
Bartholomew, D., Steel, F., Moustaki, I. and Galbraith, J. (2002) The Analysis and Interpretation of Multivariate Data for Social Scientists. London: Chapman and Hall.
#library(ltm)
#library(mirt)Logistic distribution:
IRTmodel <- ltm(LSAT~z1,IRT.param= TRUE)IRTmodel <- ltm(LSAT~z1,IRT.param= TRUE)
summary(IRTmodel)##
## Call:
## ltm(formula = LSAT ~ z1, IRT.param = TRUE)
##
## Model Summary:
## log.Lik AIC BIC
## -2466.653 4953.307 5002.384
##
## Coefficients:
## value std.err z.vals
## Dffclt.Item 1 -3.3597 0.8669 -3.8754
## Dffclt.Item 2 -1.3696 0.3073 -4.4565
## Dffclt.Item 3 -0.2799 0.0997 -2.8083
## Dffclt.Item 4 -1.8659 0.4341 -4.2982
## Dffclt.Item 5 -3.1236 0.8700 -3.5904
## Dscrmn.Item 1 0.8254 0.2581 3.1983
## Dscrmn.Item 2 0.7229 0.1867 3.8721
## Dscrmn.Item 3 0.8905 0.2326 3.8281
## Dscrmn.Item 4 0.6886 0.1852 3.7186
## Dscrmn.Item 5 0.6575 0.2100 3.1306
##
## Integration:
## method: Gauss-Hermite
## quadrature points: 21
##
## Optimization:
## Convergence: 0
## max(|grad|): 0.024
## quasi-Newton: BFGS
coef(IRTmodel)## Dffclt Dscrmn
## Item 1 -3.3597341 0.8253715
## Item 2 -1.3696497 0.7229499
## Item 3 -0.2798983 0.8904748
## Item 4 -1.8659189 0.6885502
## Item 5 -3.1235725 0.6574516
The Difficulty is analagous to θ and 'ability'. The figures are <0 and in this respect the questions are 'easy'.
Discrimination describes how well the question discriminates ability; in this context a good discriminator would be >1; these questions are poor discriminators.
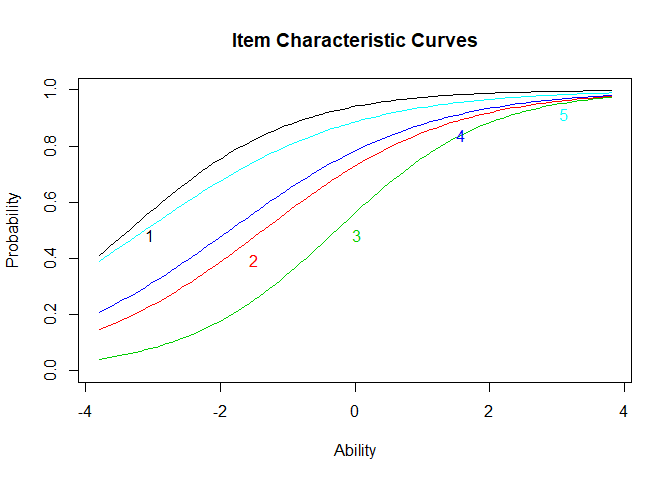
plot(IRTmodel, type="ICC")S curves would be optimal but the tails are missing.
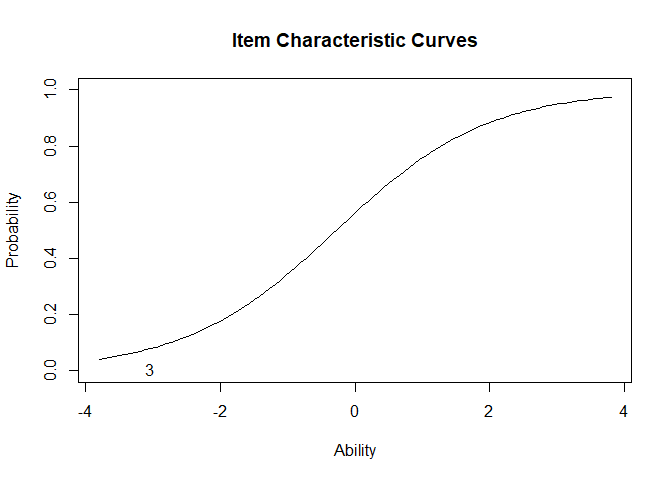
plot(IRTmodel, type ="ICC",items=3)Curve 3 is the most representative of an S curve and this item is the best discrimator of ability.
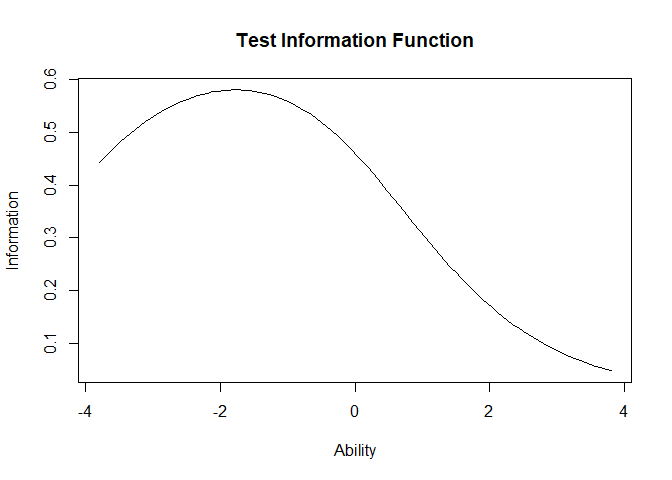
plot(IRTmodel, type ="IIC",items=0) factor.scores(IRTmodel)##
## Call:
## ltm(formula = LSAT ~ z1, IRT.param = TRUE)
##
## Scoring Method: Empirical Bayes
##
## Factor-Scores for observed response patterns:
## Item 1 Item 2 Item 3 Item 4 Item 5 Obs Exp z1 se.z1
## 1 0 0 0 0 0 3 2.277 -1.895 0.795
## 2 0 0 0 0 1 6 5.861 -1.479 0.796
## 3 0 0 0 1 0 2 2.596 -1.460 0.796
## 4 0 0 0 1 1 11 8.942 -1.041 0.800
## 5 0 0 1 0 0 1 0.696 -1.331 0.797
## 6 0 0 1 0 1 1 2.614 -0.911 0.802
## 7 0 0 1 1 0 3 1.179 -0.891 0.803
## 8 0 0 1 1 1 4 5.955 -0.463 0.812
## 9 0 1 0 0 0 1 1.840 -1.438 0.796
## 10 0 1 0 0 1 8 6.431 -1.019 0.801
## 11 0 1 0 1 1 16 13.577 -0.573 0.809
## 12 0 1 1 0 1 3 4.370 -0.441 0.813
## 13 0 1 1 1 0 2 2.000 -0.420 0.813
## 14 0 1 1 1 1 15 13.920 0.023 0.828
## 15 1 0 0 0 0 10 9.480 -1.373 0.797
## 16 1 0 0 0 1 29 34.616 -0.953 0.802
## 17 1 0 0 1 0 14 15.590 -0.933 0.802
## 18 1 0 0 1 1 81 76.562 -0.506 0.811
## 19 1 0 1 0 0 3 4.659 -0.803 0.804
## 20 1 0 1 0 1 28 24.989 -0.373 0.815
## 21 1 0 1 1 0 15 11.463 -0.352 0.815
## 22 1 0 1 1 1 80 83.541 0.093 0.831
## 23 1 1 0 0 0 16 11.254 -0.911 0.802
## 24 1 1 0 0 1 56 56.105 -0.483 0.812
## 25 1 1 0 1 0 21 25.646 -0.463 0.812
## 26 1 1 0 1 1 173 173.310 -0.022 0.827
## 27 1 1 1 0 0 11 8.445 -0.329 0.816
## 28 1 1 1 0 1 61 62.520 0.117 0.832
## 29 1 1 1 1 0 28 29.127 0.139 0.833
## 30 1 1 1 1 1 298 296.693 0.606 0.855
Empirical Bayes scoring
Where z1 is the predicted ability based on the pattern of scores. Most common combination is to get them all right (298), questions are too easy.
IRTmodel_guess=tpm(LSAT,type="latent.trait",IRT.param = TRUE)factor.scores(IRTmodel_guess)##
## Call:
## tpm(data = LSAT, type = "latent.trait", IRT.param = TRUE)
##
## Scoring Method: Empirical Bayes
##
## Factor-Scores for observed response patterns:
## Item 1 Item 2 Item 3 Item 4 Item 5 Obs Exp z1 se.z1
## 1 0 0 0 0 0 3 2.230 -1.871 0.790
## 2 0 0 0 0 1 6 5.820 -1.463 0.792
## 3 0 0 0 1 0 2 2.583 -1.446 0.793
## 4 0 0 0 1 1 11 8.944 -1.032 0.796
## 5 0 0 1 0 0 1 0.701 -1.325 0.796
## 6 0 0 1 0 1 1 2.628 -0.908 0.800
## 7 0 0 1 1 0 3 1.185 -0.889 0.801
## 8 0 0 1 1 1 4 5.969 -0.463 0.809
## 9 0 1 0 0 0 1 1.855 -1.438 0.801
## 10 0 1 0 0 1 8 6.456 -1.017 0.803
## 11 0 1 0 1 1 16 13.583 -0.570 0.810
## 12 0 1 1 0 1 3 4.374 -0.439 0.814
## 13 0 1 1 1 0 2 2.002 -0.418 0.815
## 14 0 1 1 1 1 15 13.906 0.028 0.829
## 15 1 0 0 0 0 10 9.438 -1.358 0.791
## 16 1 0 0 0 1 29 34.655 -0.945 0.796
## 17 1 0 0 1 0 14 15.612 -0.926 0.797
## 18 1 0 0 1 1 81 76.691 -0.504 0.806
## 19 1 0 1 0 0 3 4.684 -0.801 0.800
## 20 1 0 1 0 1 28 25.037 -0.375 0.810
## 21 1 0 1 1 0 15 11.481 -0.354 0.811
## 22 1 0 1 1 1 80 83.338 0.089 0.827
## 23 1 1 0 0 0 16 11.294 -0.909 0.803
## 24 1 1 0 0 1 56 56.131 -0.481 0.811
## 25 1 1 0 1 0 21 25.652 -0.460 0.812
## 26 1 1 0 1 1 173 173.188 -0.018 0.825
## 27 1 1 1 0 0 11 8.446 -0.329 0.816
## 28 1 1 1 0 1 61 62.389 0.119 0.831
## 29 1 1 1 1 0 28 29.073 0.142 0.832
## 30 1 1 1 1 1 298 296.893 0.612 0.853
anova(IRTmodel,IRTmodel_guess) ## Warning in anova.ltm(IRTmodel, IRTmodel_guess): either the two models are not nested or the model represented by 'object2' fell on a local maxima.
##
## Likelihood Ratio Table
## AIC BIC log.Lik LRT df p.value
## IRTmodel 4953.31 5002.38 -2466.65
## IRTmodel_guess 4963.32 5036.94 -2466.66 -0.01 5 1
Addition of guessing parameter does not improve the model,illustrated by log likelihood. There is no significant variance between 2PL and 3PL.