C++ classes for single and multidimensional non-parametric Gaussian kernel regression. These objects allow for the fitting of smooth profiles through noisy data. The functions that solve for the profile are embarrassingly parallel and use OpenMP to gain large speedups.
License: GNU General Public License, version 3. See the LICENSE file.
Dependencies: STL and OpenMP
Exceptions:
The KernelFit objects will throw KernelFitError when given unacceptable
inputs for the constructors.
The header and source file, KernelFit.hh and KernelFit.cc, respectively are located in the Source directory. The user should simply put the header file with the other header files for their project and compile, link the source file with their other source files. The Makefile included with this repository compiles and runs the test programs TestKernelFit1D.cc and TestKernelFit2D.cc in the Test directory. The figures included below represent the results of those programs.
Notice:
The TestKernelFit2D.cc program took ~ 2 min to run on my MacBook Pro (Intel i5)
using 4 threads. This program (in addition to the other test program) will be
run automatically when make is executed.
After included the code in your project, you can use them similar to the below snippet:
#include <KernelFit.hh>...
omp_set_num_threads(4);...
KernelFit1D<double> kernel(x, y, bandwidth);
std::vector<double> profile = kernel.Solve(new_x);Include the header file (snippet 1). If you don't specify the desired maximum
thread count with OpenMP (snippet 2), the Solve() method will choose for you.
In the last snippet, we create the kernel object with three arguments. The first
two, x and y are std::vector<double>s and the last argument should be of
the same type but is a scalar. new_x should be similar to x and y but a
new line-space that you want to solve on.
The general approach here is described quite
well on the Kernel Smoother
Wikipedia page. Here, bandwidth refers to the length scale, or explicitly,
the standard deviation in the Gaussian. Choosing the correct bandwidth here is
critical to getting a good fit. If your choice is too small, you'll essentially
be drawing strait lines between the data points. If your bandwidth is too large,
everybody will be under the Gaussian together and we'll have almost a flat line
with a height of the average value of the data set.
As is evident by the last code snippet, the objects are template defined. At this point, the only available type is double. In order to use different types simply add the following line to the bottom of KernelFit.cc
template class KernelFit<float>;where float was the desired type.
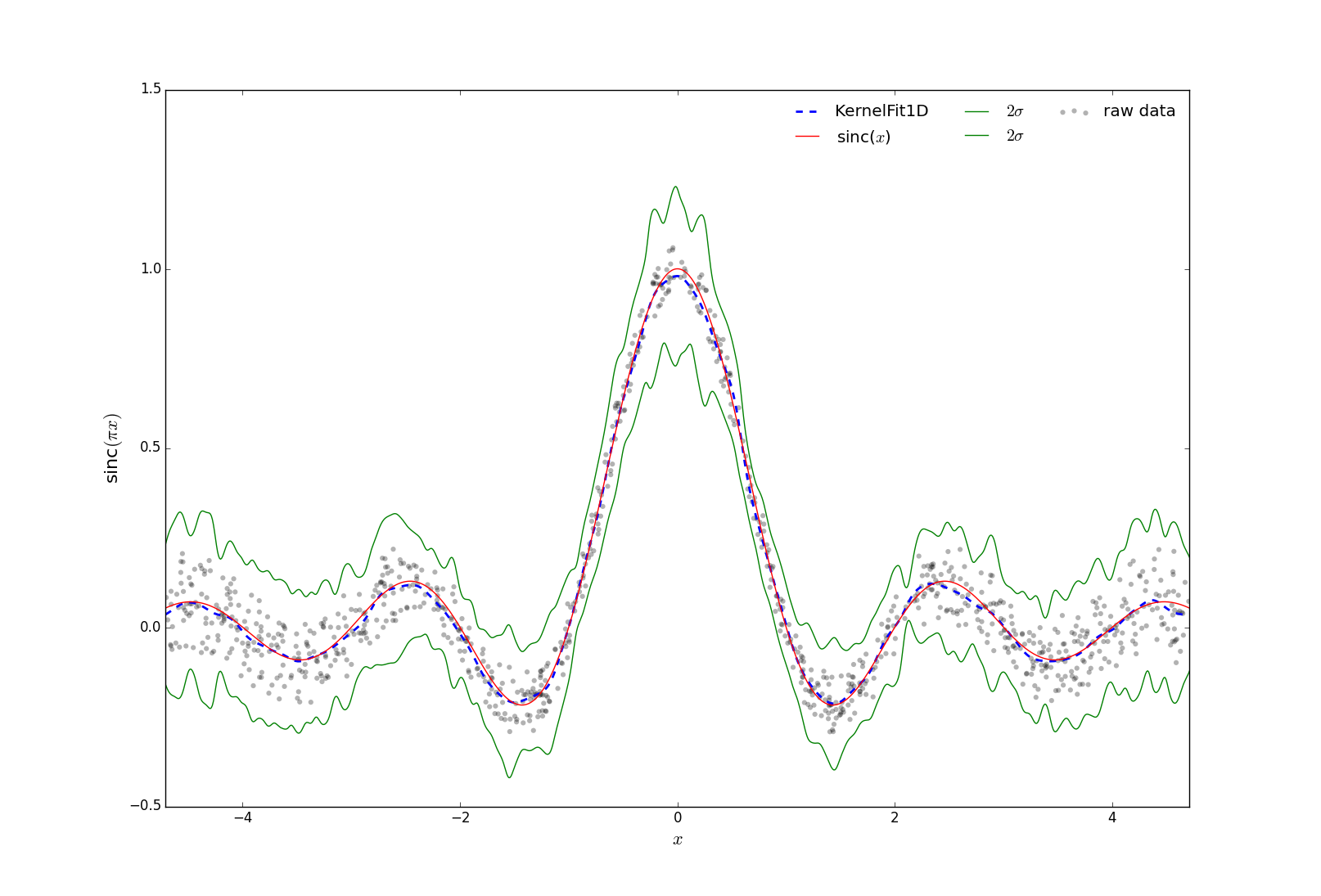
Figure 1: The above figure was plotting using Python and showcases the results of the TestKernelFit1D.cc program. A noisy sinc function was produced with both red and white noise. The blue dashed line demonstrates the smooth profile fit through the data. The red dashed line shows the analytical function.
The usage for a 2D surface profile is very similar:
KernelFit2D<double> kernel(x, y, z, bandwidth);
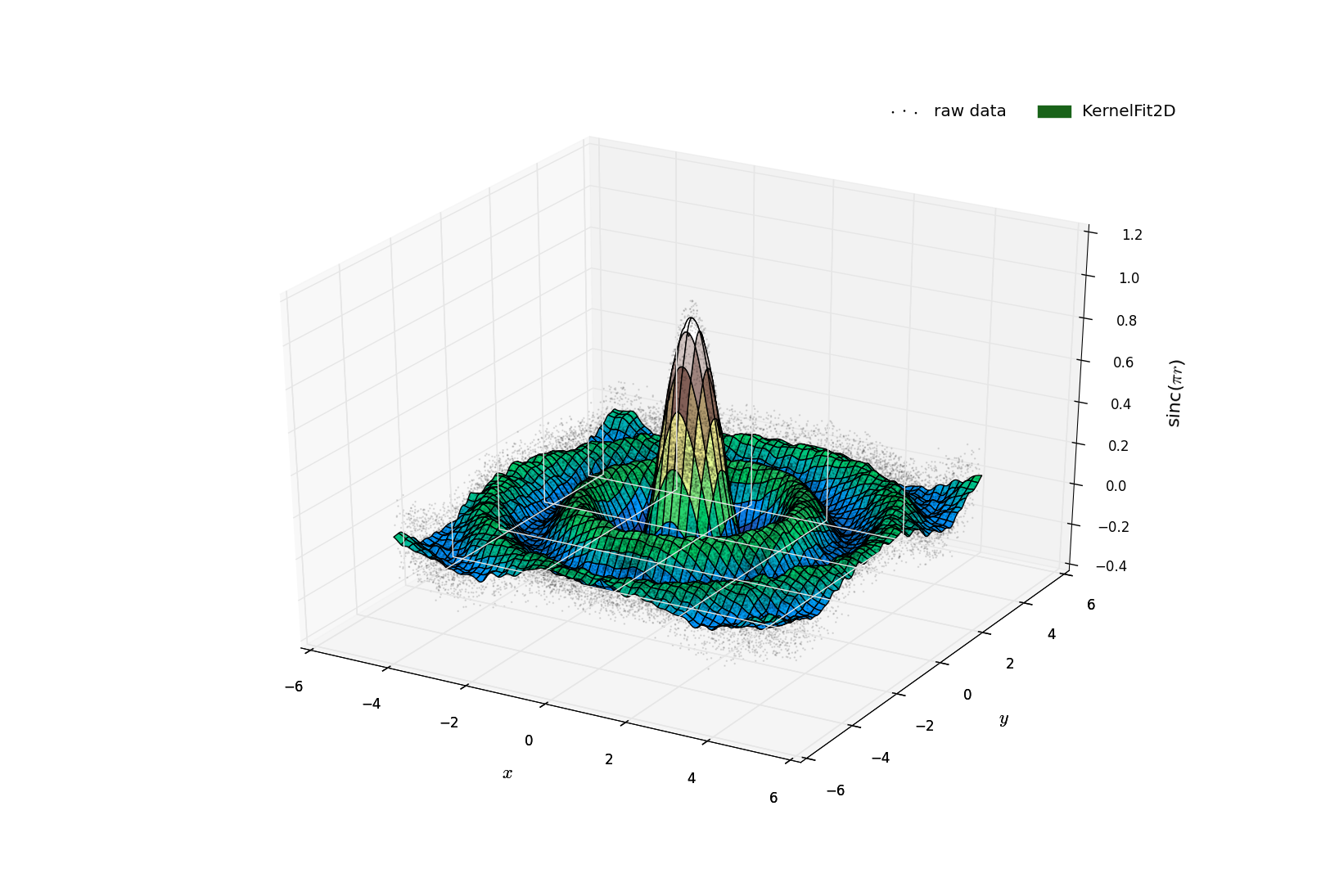
std::vector<std::vector<double>> profile = kernel.Solve(new_x, new_y);Figure 2: The above figure was plotting using Python and showcases the results of the TestKernelFit2D.cc program. Just as in the example in Figure 1, A sinc function was used here as well but radially. The brown-red scatter points are the raw data produced. The terrain colored mesh grid showcases the smooth surface profile generated by the KernelFit2D algorithm.
Geoffrey Lentner
Graduate Research Assistant
Department of Physics & Astronomy
University of Louisville
website: glentner.github.io