IB Math AA HL Internal Assessment - May 2023

Introduction

This repository contains the scripts and document for my Internal Assessment in Mathematics: Analysis and Approaches at Higher Level as part of the International Baccalaureate Diploma Programme. I submitted this IA in the M23 Session and ultimately received a 7 for this course although I do not know exacty how much the IA influenced this result as the exams account for a majority of the final grade.

The IA is entitled Investigating Optimal Strategies in the Dice Game 'Snake Eyes', and as the title implies, concerns a simple dice game known as snake eyes. I decided to investigate two main strategies and compare them using calculations as well as simulations written in python to validate validate that the calculations were not erroneous. Additionally I extended my investigation with biased dice to observe how that affected the strategies.

A Summary of the Results

This is a summary of the contents of this document.

The rules of the game

The game can be played by two or more players, where the winner reaches a total score of 100 points. The player can roll as many times as they wish in a single turn, with the turn’s total score being the sum of dice of each roll within the turn. Yet, there are some limitations, which are as follows:

The roll’s sum will only be counted if neither of the dice rolls a ‘1’
The roll’s sum will not be counted to the total if during the turn any dice rolls a ‘1’
If both dice roll a ‘1’ during a turn, the players total score gets reset to zero

Shown visually, here are the score outcomes of a single roll accompanied by a table showing the proability distribution and its expected value $E(X_1)$.

$$E(X_1) = \sum_{x=0}^{12} x \times P(X_1=x) = \frac{50}{9} \approx 5.56$$

Strategy 1: Optimal Target Roll Quantity

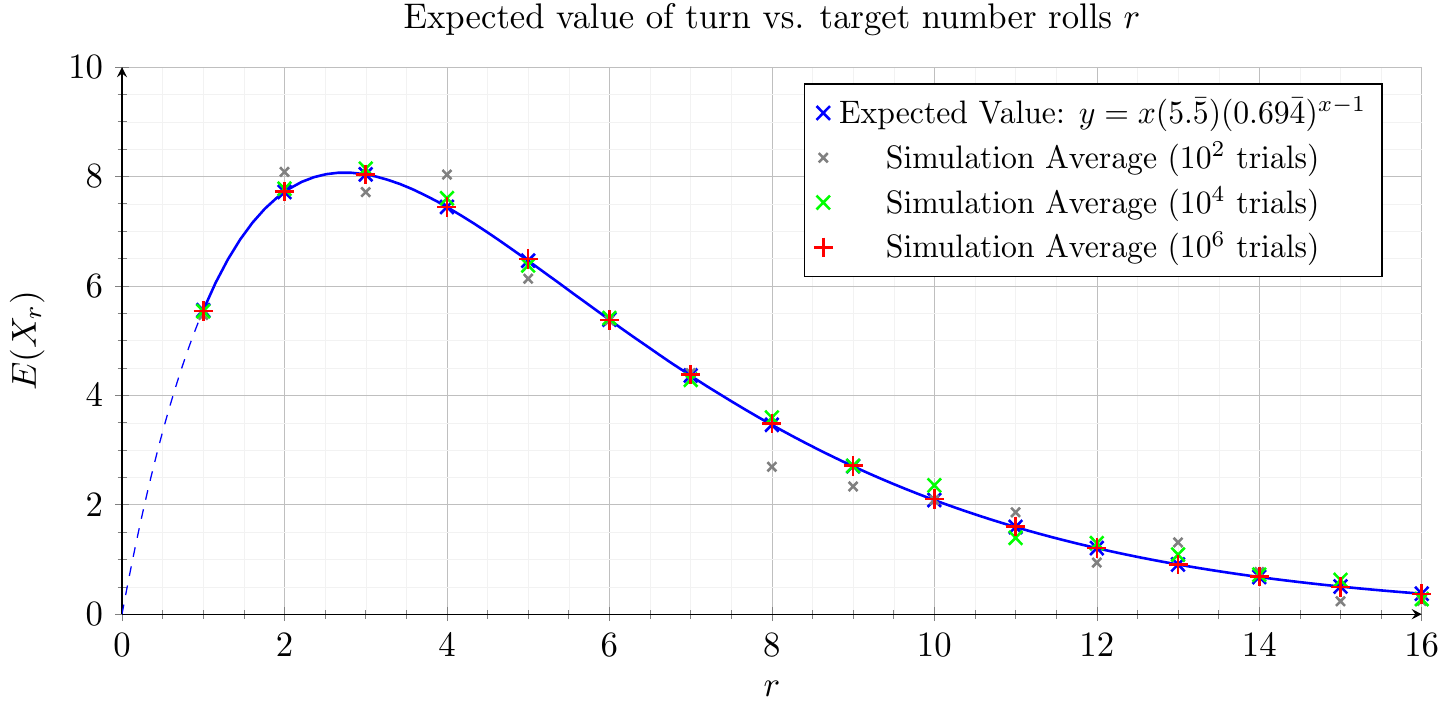
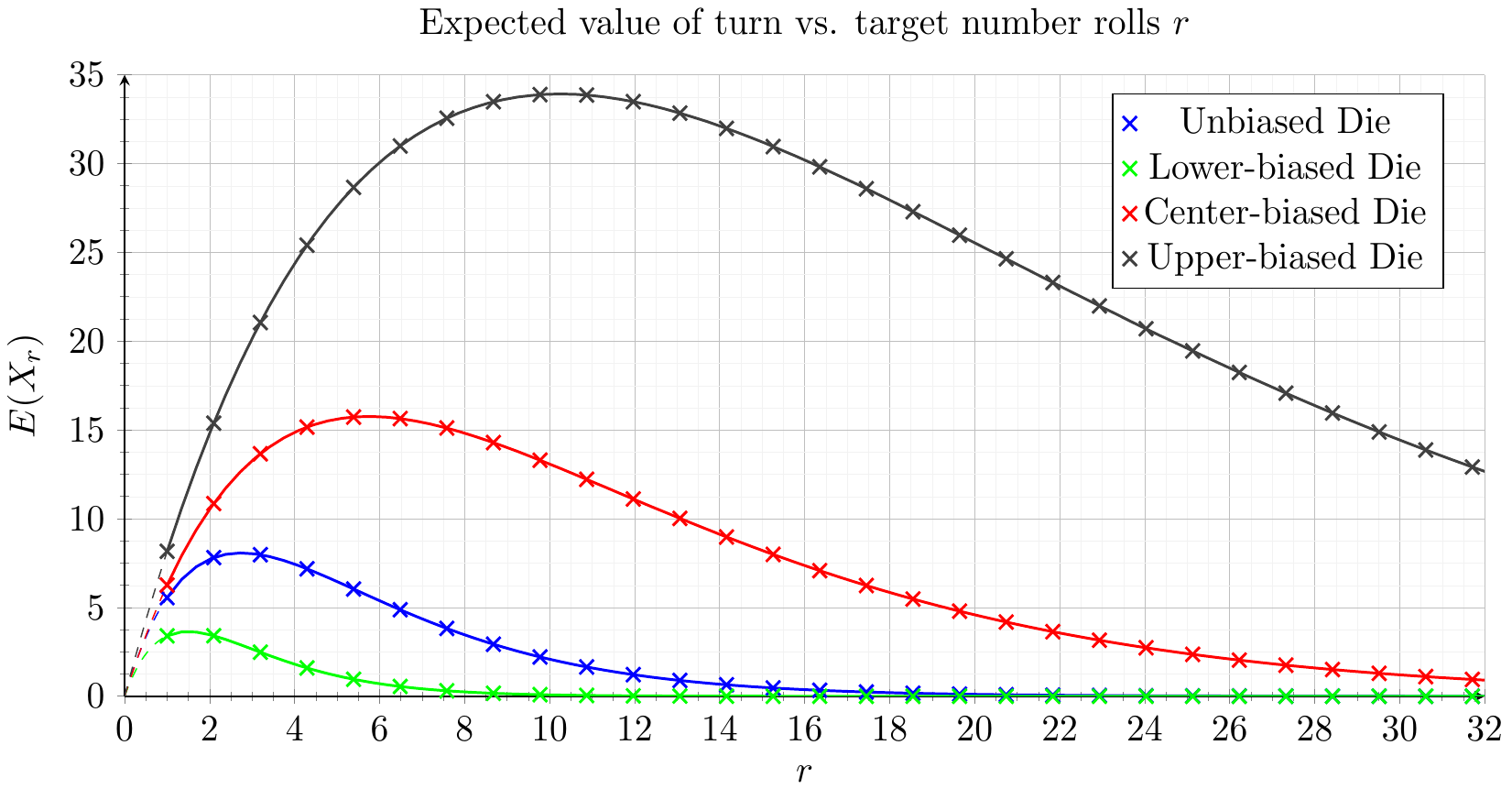
A simple equation can be derived to find the expected value of a single turn given a target number of rolls. This is a simple strategy in which the player keeps rolling until they either reach their target score or they lose.

$$E(X_r) = E(X_1) \cdot r\left( 1 - p(0) \right)^{r-1}$$

This can then be plotted on a graph along with the results of a simulation:

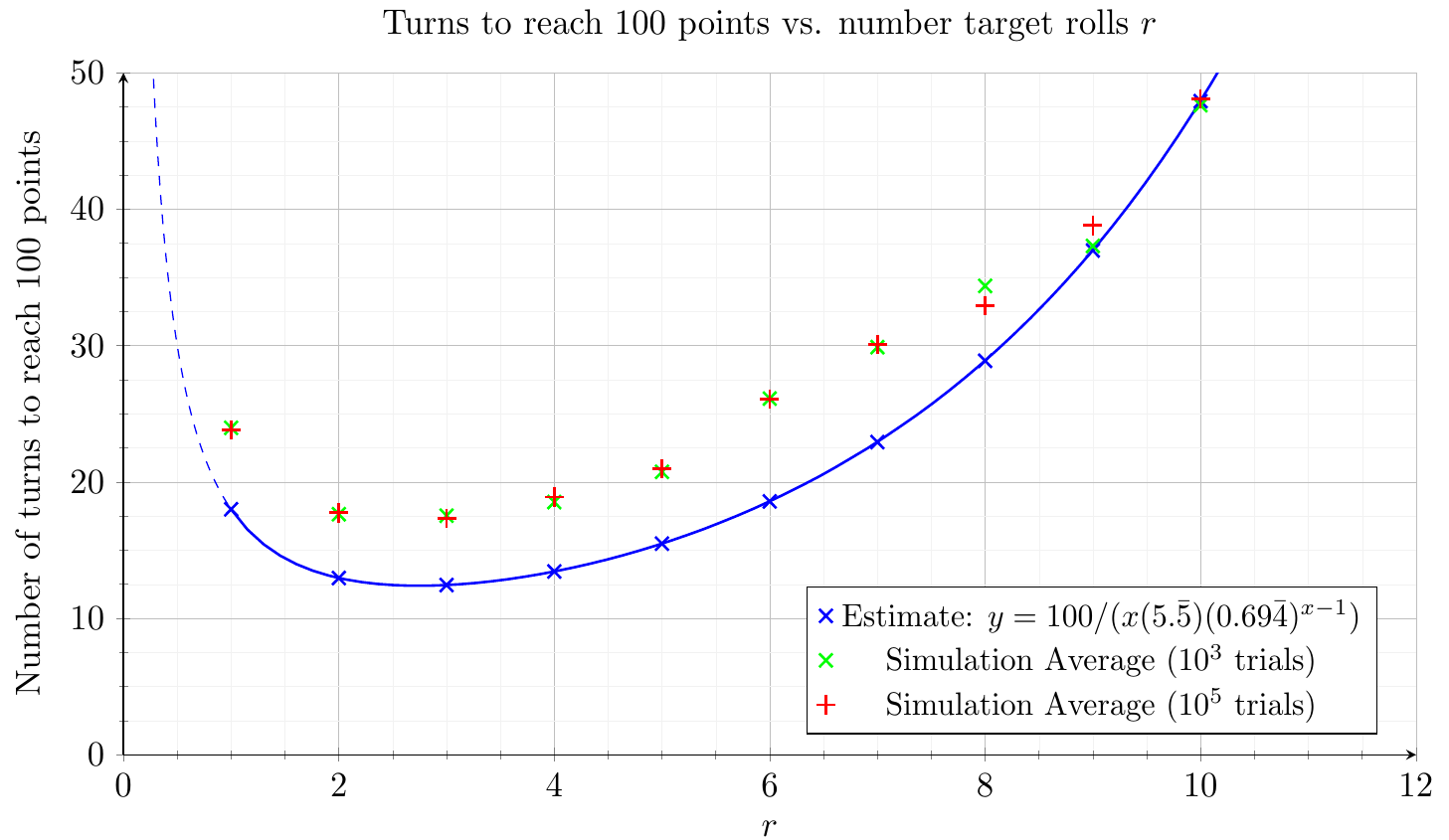
Using this, we can estimate the amount of rolls needed to win a game: $$\text{Estimated turns to win} = \frac{100}{E(X_1) \cdot r\left( 1 - \frac{11}{36} \right)^{r-1}}$$

Finally the average amount of rolls required to win a game can be plotted and the minimum can be observed which will be the optimal target roll quantity, which turns out to be 3 rolls.

Strategy 2: Optimal Target Score

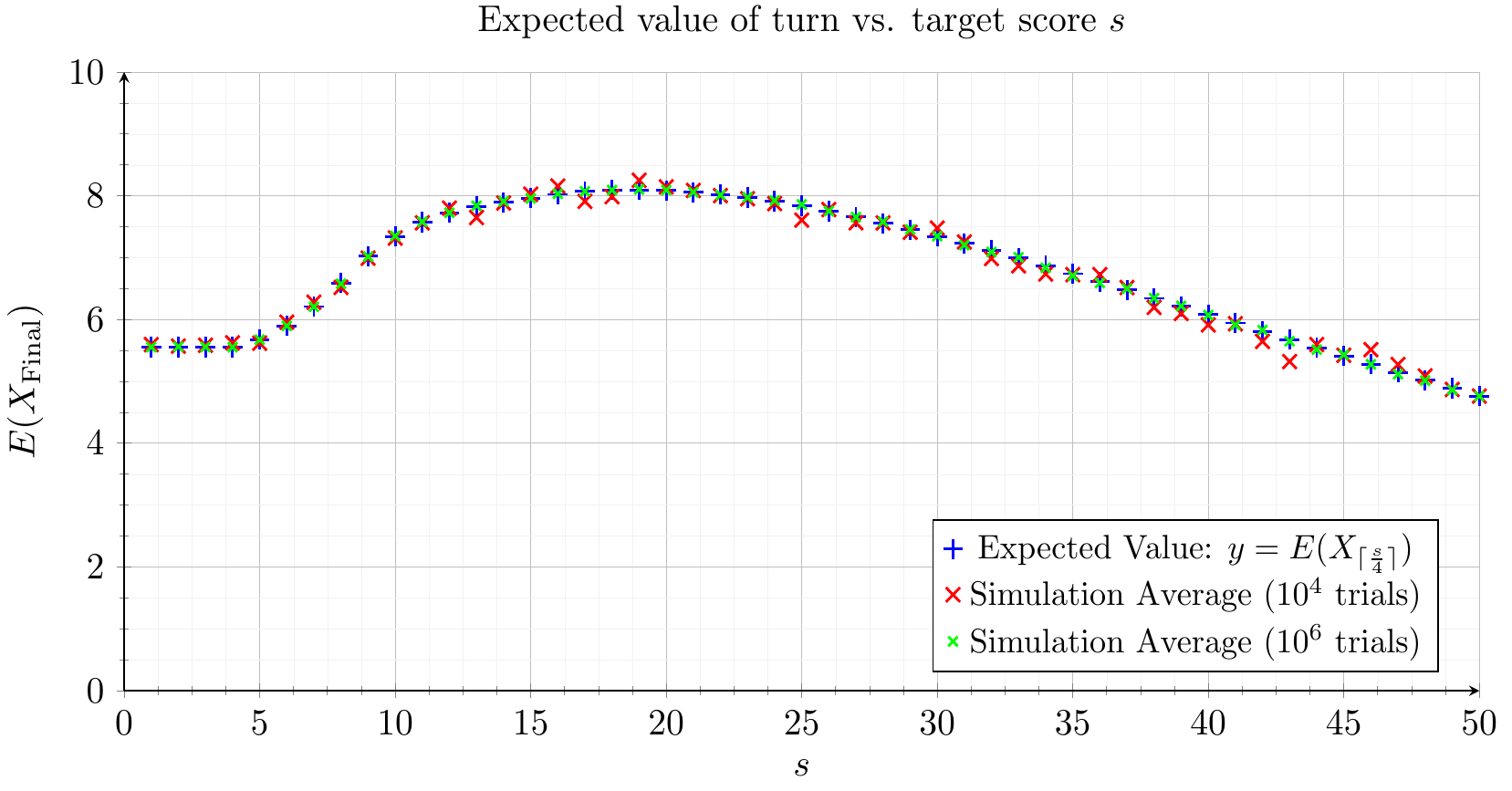
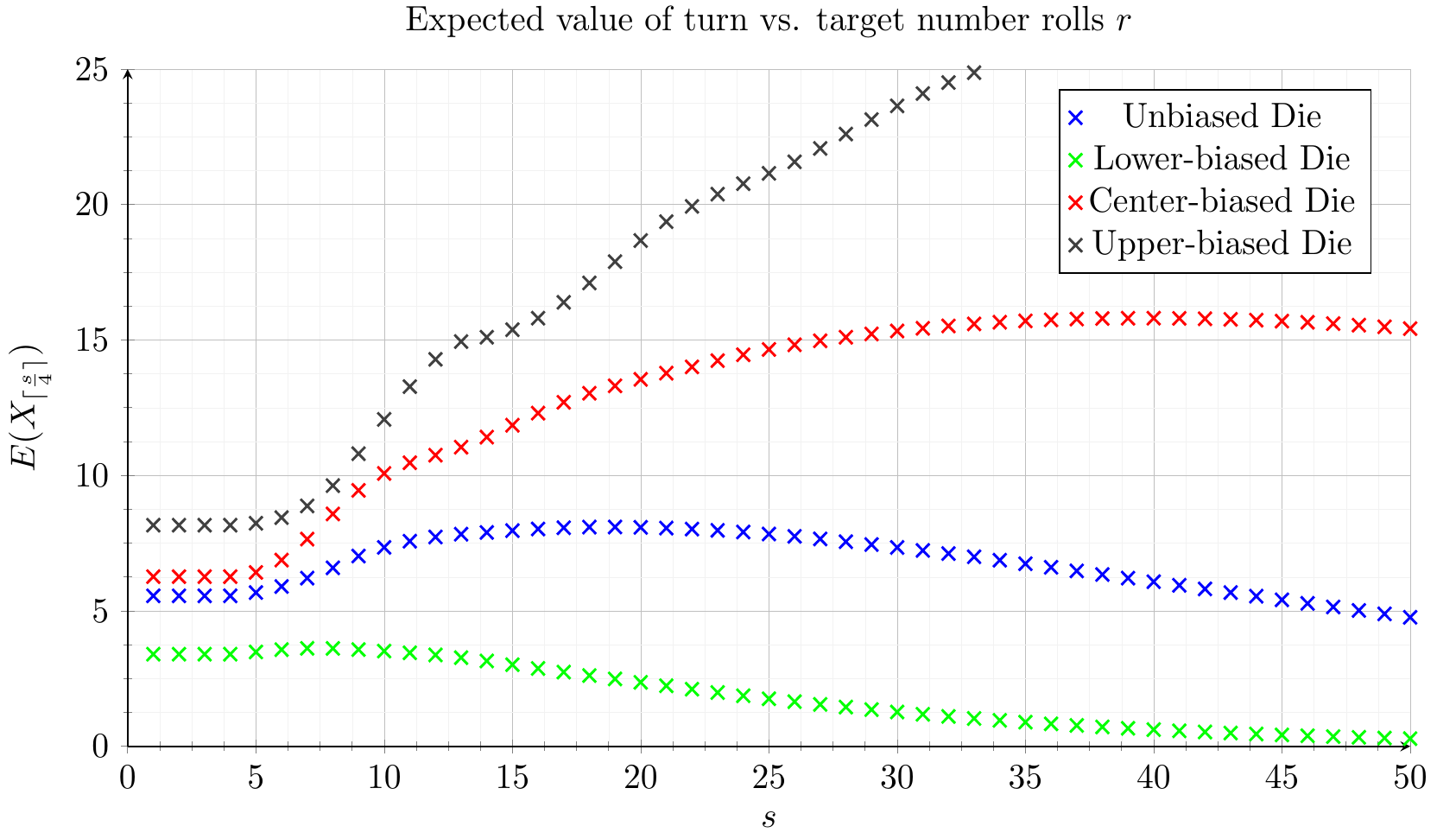
Another equation can be derived to find the expected value of a single turn given a target score. With this strategy the player keeps rolling until they reach a certain score at which point they stop rolling.

$$P(X_r = x) = \begin{dcases} P(X_{r-1}=0) + p(0)\cdot\sum_{i=4(t-1)}^{12(t-1)}P(X_{r-1}=i) & \text{if $x=0$} \\\ \sum_{i=\max(x-12, 4)}^{x-4} P(X_{r-1}=i) \cdot p(x-i) & \text{if $0 < x < s$} \\\ P(X_{r-1}=x) + \sum_{i=\max(x-12,4)}^{\min(x-4, s-1)} P(X_{r-1}=i) \cdot p(x-i) & \text{if $s \leq x < s+12$} \\\ 0 & \text{otherwise} \end{dcases}$$

$$E(X_u) = \sum_{i=s}^{s+12} i \cdot P(X_u=i) \qquad u= \lceil \frac s 4 \rceil \text{ (upper bound of rolls)}$$$$

Again this can be plotted on a graph along with some results from the simulation:

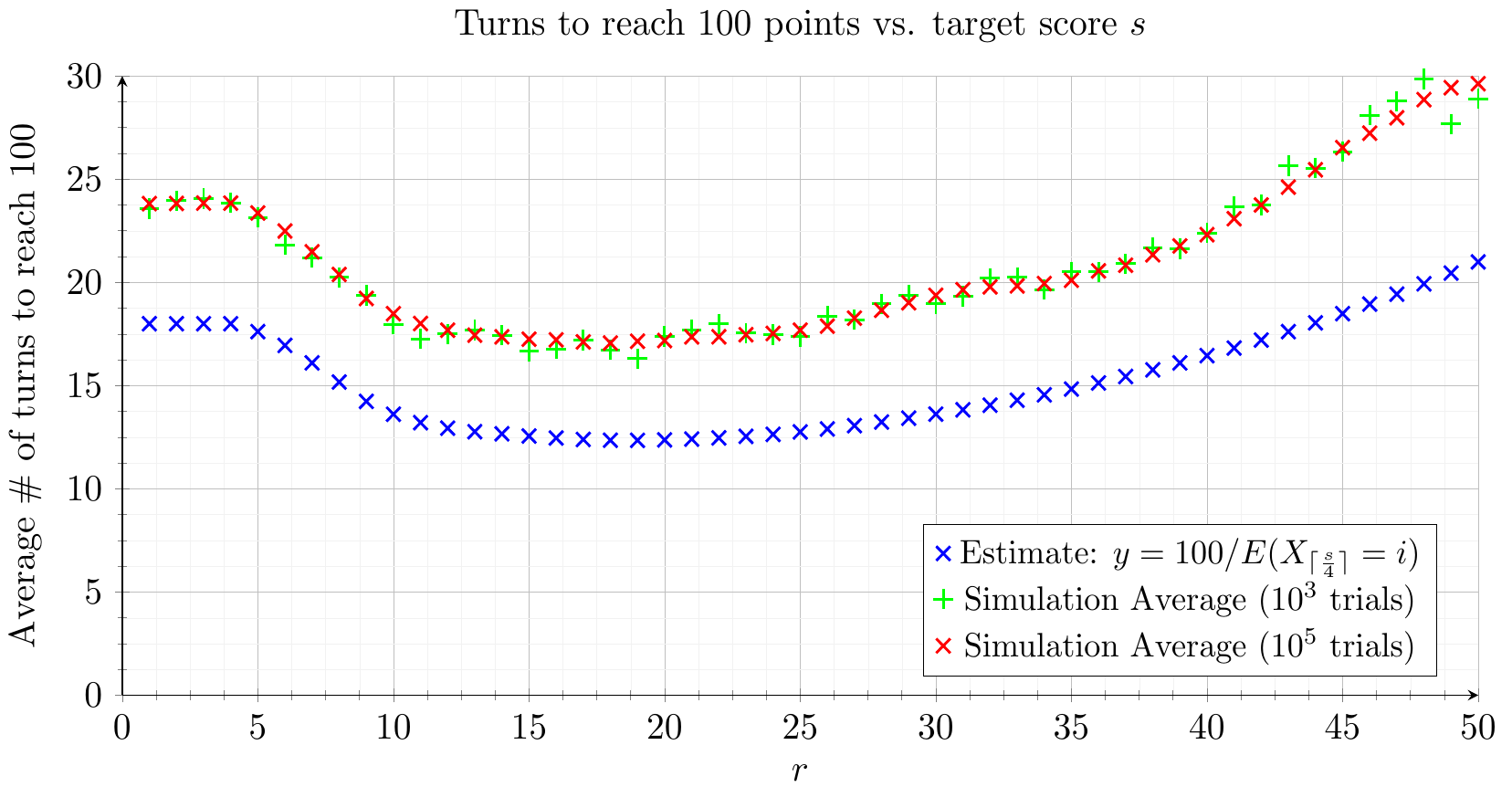
Next an game can be simulated to determine the optimal target score to minimise the number of turns required to win the game. Again this can be plotted on a graph along with some results from the simulation:

As can be seen from both plots, the optimal target score is 19.

Effects of Biased Dice

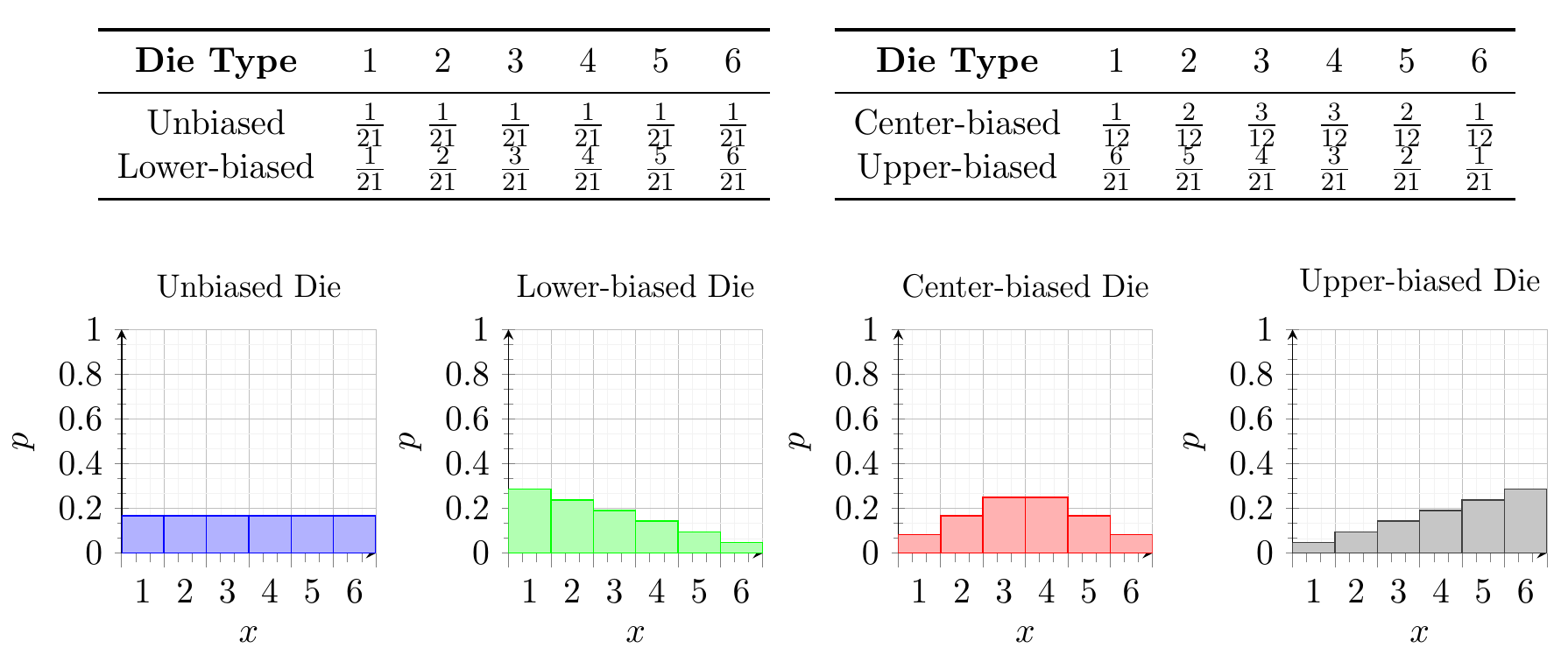
I thought it would be interesting to see if biased dice affected, so I generated the following probability distributions:

This had the following effects on the optimal target rolls and target scores:

It can be seen that dice that are weighted towards higher values have much higher expected values, but also at higher numbers of target rolls. This is to be expected as the probability of rolling a 1 is lower, meaning that there is a lower risk of losing the turn or rolling snake eyes. Specifically, the optimal score for the lower-biased dice is $r = 2$, unbiased dice is $r = 3$, center-biased die is $r = 6$, and upper-biased die is $r = 10$.

As seen in the plot, the dice biased upwards have much higher expected values and occur at higher target scores, which was also the case with target rolls. The lower-biased die peaks at s = 8, the unbiased at $s = 19$, the center-biased at $s = 41$, and the upper-biased (not shown on plot) peaks at $s = 88$.

Running the Scripts

This repository contains a bash script called gen.sh which will run each type of die bias. This script works by (crudely) commenting and uncommenting lines in the sampling.py script so in case of any errors or interruptions, the comments may have to be reset.

This script will also take a while to run, taking 1h 15m on my i5-8265U processor with 8GB RAM.

Requirements

This script requires the following libraries to be installed:

numpy - mathematical computations
numba - JIT complilation acceleration
pandas - data handling
tqdm - terminal progress bars

This should work with with any version of python, as long as the libraries support it. It's always good to check what version of python numba uses since that usually causes the most problems.

Citations

References can be found in the pdf, but I also added the references.bib file to the repository. Here is a list of the sources I used in URL form: