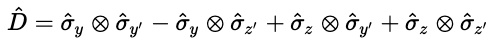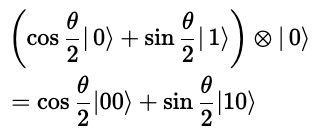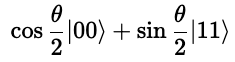Qiskitライブラリを使い、CHSH不等式を量子ゲート回路でシミュレーションするプログラム
Pythonは、Version 3.6以上が必要です。(私は3.8.12で確認しました)
Qiskitをインストールする必要があります https://qiskit.org/
% pip install 'qiskit[visualization]'
実行するには
% python chsh_inequality.py
を実行するだけです。初期状態を決めるパラメータθ(後述)を-π〜+πの範囲で少しずつ変えながら、各θに対して 10000 回シミュレーションを行います。
数値計算結果と、グラフが表示されて終わります。
-3.141592653589793 1.4026
-2.9804853380210856 1.6760000000000002
-2.8193780224523786 1.8388
-2.658270706883671 2.0974000000000004
...
2.6582707068836706 0.7478
2.819378022452378 0.9572
2.9804853380210856 1.1806
3.141592653589793 1.4108
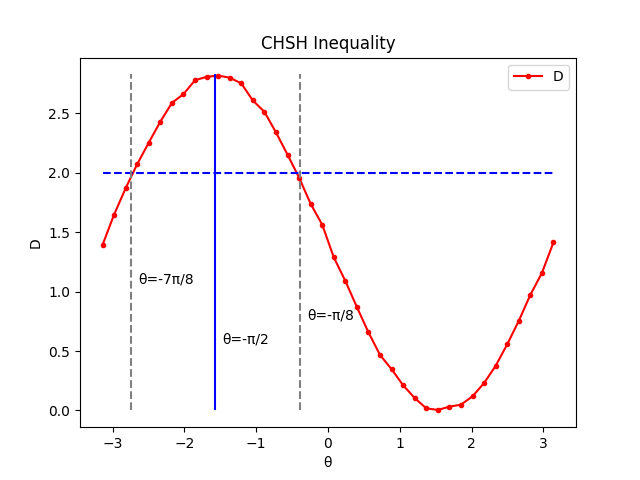
グラフをみると、パラメータθが -7π/8〜-π/8のあたりでDが2.0を超えていることが分かります。 (古典論ではベルの不等式が成り立つため、どれだけ相関が強くても |D| が2.0を超えることはあり得ない)
なお、理論値はθが-π/2のときで、そのときの値は2√2です。図では青い縦線を引いたところが、θ=-π/2になります。 理論値をほぼ再現していることが分かります。
CHSH不等式のD
を、量子ゲート回路を使ってシミュレーションしています。
このシミュレーションでは簡単のため、2量子ビットの初期状態を、θをパラメータとして、
で作成しました。(この時点でかなり作為的ではありますが、あまりパラメータが多いとプロットできないので、今回はパラメータはθだけにしました。このため、θの値によってDは上限値 2√2になりますが、θを変えるだけではDは下限値 -2√2にはなりません。下限値も出すためには、初期状態をもう少し工夫して作る必要があります)
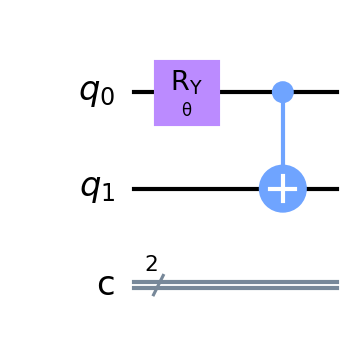
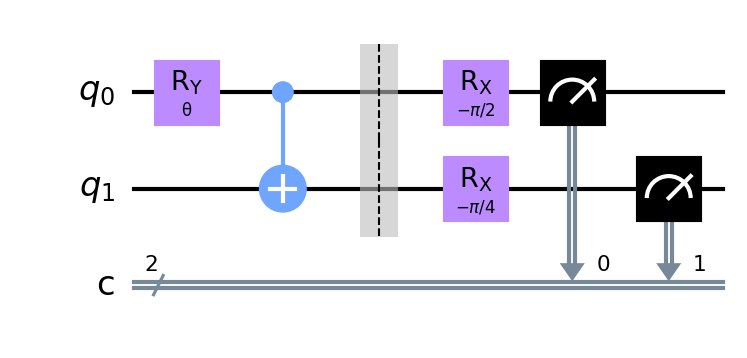
この図の一番左側の生成された直後のq_0, q_1はそれぞれ |0〉 状態です。つまり|q_0〉⊗ |q_1〉= |q_0 q_1〉= |00〉状態です。これに、次の2つの回路を適用して、初期状態を作成しています。
1つ目の回路は、y軸周りの回転を行うR_y(θ)回路。この回路により第0ビットはy軸周りにθ回転します。なお、空間回転としてはθなのですが、スピンの回転としてはθ/2になることに注意して下さい。これは、空間での360回転は、スピンでは180回転(つまり、|0〉と|1〉がそれぞれ -|0〉と-|1〉になるだけ)になることに相当します。よって、この回路により状態は
となります。
2つ目の回路は、制御Not回路です。第0ビットが1のときだけ、第1ビットを反転させます。これを適用することにより、
という状態が作成されます。
これを、今回の実験(シミュレーション)の初期状態として採用します。量子もつれ状態です。
この2量子ビットの状態について、Aliceは第0ビット、Bobは第1ビットを計測したいのです。
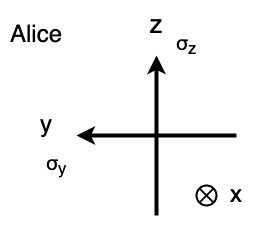
Aliceが計測したいのは、第0ビットのz方向のスピン(σ_z)または、第0ビットのy方向のスピン(σ_y) のどちらかです。(量子論のため、アリスは、z方向とy方向のスピンを両方を同時には計測出来ません)
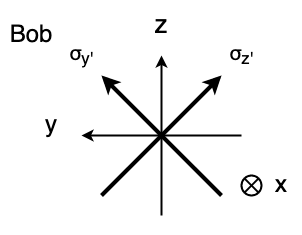
Bobが計測したいのは、第1ビットのz'方向のスピン(σ_z')または、第1ビットのy'方向のスピン(σ_y')のどちらかです。z'方向とy'方向は、z方向,y方向と比べて、(x方向に向かって) π/4回転しています。 (量子論のため、Bobもz'方向とy'方向のスピンを両方を同時には計測出来ません)
計測装置を動かすことは出来ないのですが、代わりにブロッホ球を回転させて、その回転方向で計測しています。(これは量子ビットを逆回転させていることに相当します)
注意)この座標系のとり方は、入門・現代の量子力学(堀田)のp.10の図17の右上と比べると、左右が逆に見えますが、x軸の向き(つまり前後)も逆になっているため、結局は同じ図になっています。(つまり、どちらも右手系です)
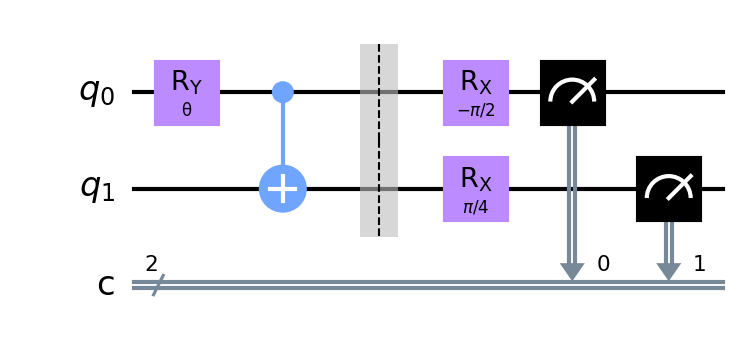
さて、それでは、Dの式の4つの項を計算するために、それぞれ個別に回路を組み立てていきます。
最終的には、古典的回路につなげて計測しています。古典回路につなくと、第0ビット、第1ビットの結果は それぞれ0または1になります。
第1項の回路で、第0ビットを0と計測したら、アリスが+1のスピンを計測したことになります。第0ビットが1と計測したなら、アリスは-1のスピンを計測したことになります。同じく、第1ビットを0と計測したら、ボブが+1のスピンを計測したことになります。第1ビットを1と計測したら、ボブは-1のスピンを計測したことになります。 そのため、(00)や(11)であれば第1項は+1、(01)や(10)であれば第1項は-1になります。
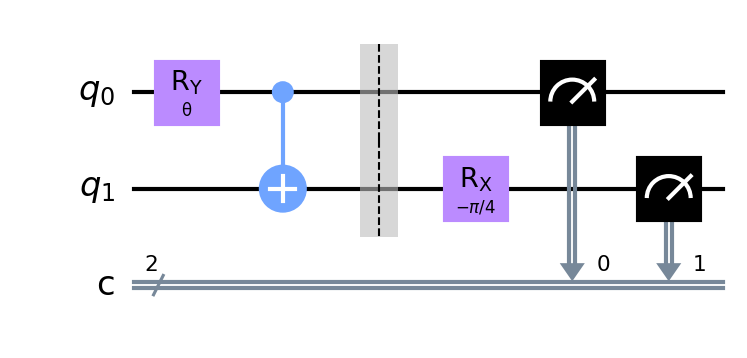
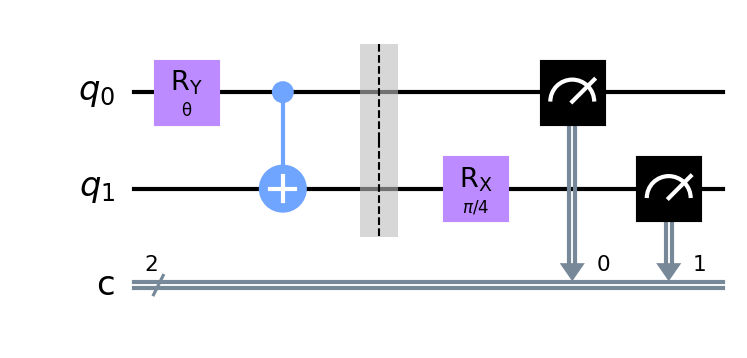
第2項の回路、第3項の回路、第4項の回路も、同様です。
各項の1回のシミュレーションでは、それぞれの回路の結果は1または-1になります。何回もシミュレーションすること によって、各項の平均値を求めることが出来ます。 (σ_zとσ_y、あるいは σ_z'とσ_y'は同時には計測出来ないので、Dを1回のシミュレーションで計算することは出来ません。しかし、Dの平均値であれば、各項ごとに平均値を求めることで求めることが出来ます)
あとは、これをいろいろなθについて、シミュレーションしていっています。
各θについて、10000回計算を行い、その平均値を出したものが、最初に示した図になります。
θ=-π/2 で D = 2√2 となりました。このとき初期状態は (|00〉-|11〉)/ √2 となるので、 入門・現代の量子力学のAppendix Aの通りの結果になっています。