Generative Adversarial Networks (GANs)

GANs were first reported on in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:

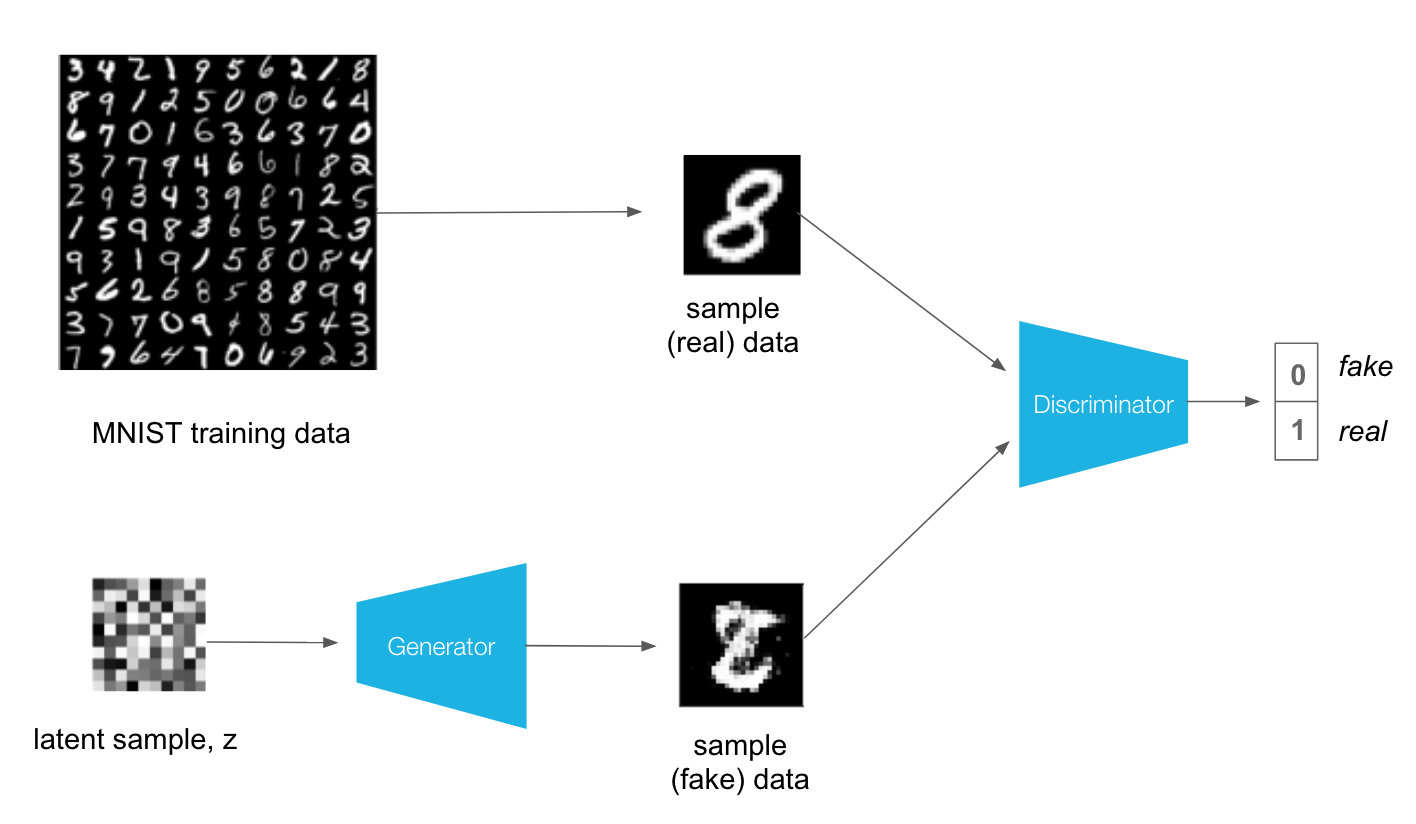
The idea behind GANs is that you have two networks, a generator G and a discriminator D, competing against each other. The generator makes "fake" data to pass to the discriminator. The discriminator also sees real training data and predicts if the data it's received is real or fake.

The generator is trained to fool the discriminator, it wants to output data that looks as close as possible to real, training data.
The discriminator is a classifier that is trained to figure out which data is real and which is fake.

What ends up happening is that the generator learns to make data that is indistinguishable from real data to the discriminator.

The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector that the generator uses to construct its fake images. This is often called a latent vector and that vector space is called latent space. As the generator trains, it figures out how to map latent vectors to recognizable images that can fool the discriminator.

If you're interested in generating only new images, you can throw out the discriminator after training.

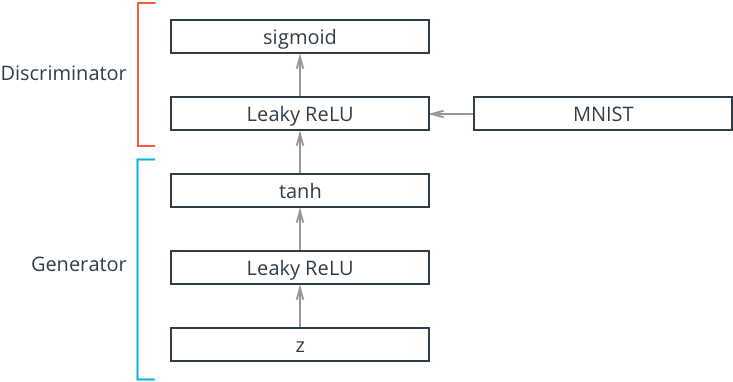
GAN Model Architecture to Generate Simple Handwritten Digits

Discriminator

The discriminator network is going to be a pretty typical linear classifier. To make this network a universal function approximator, we'll need at least one hidden layer, and these hidden layers should have one key attribute:

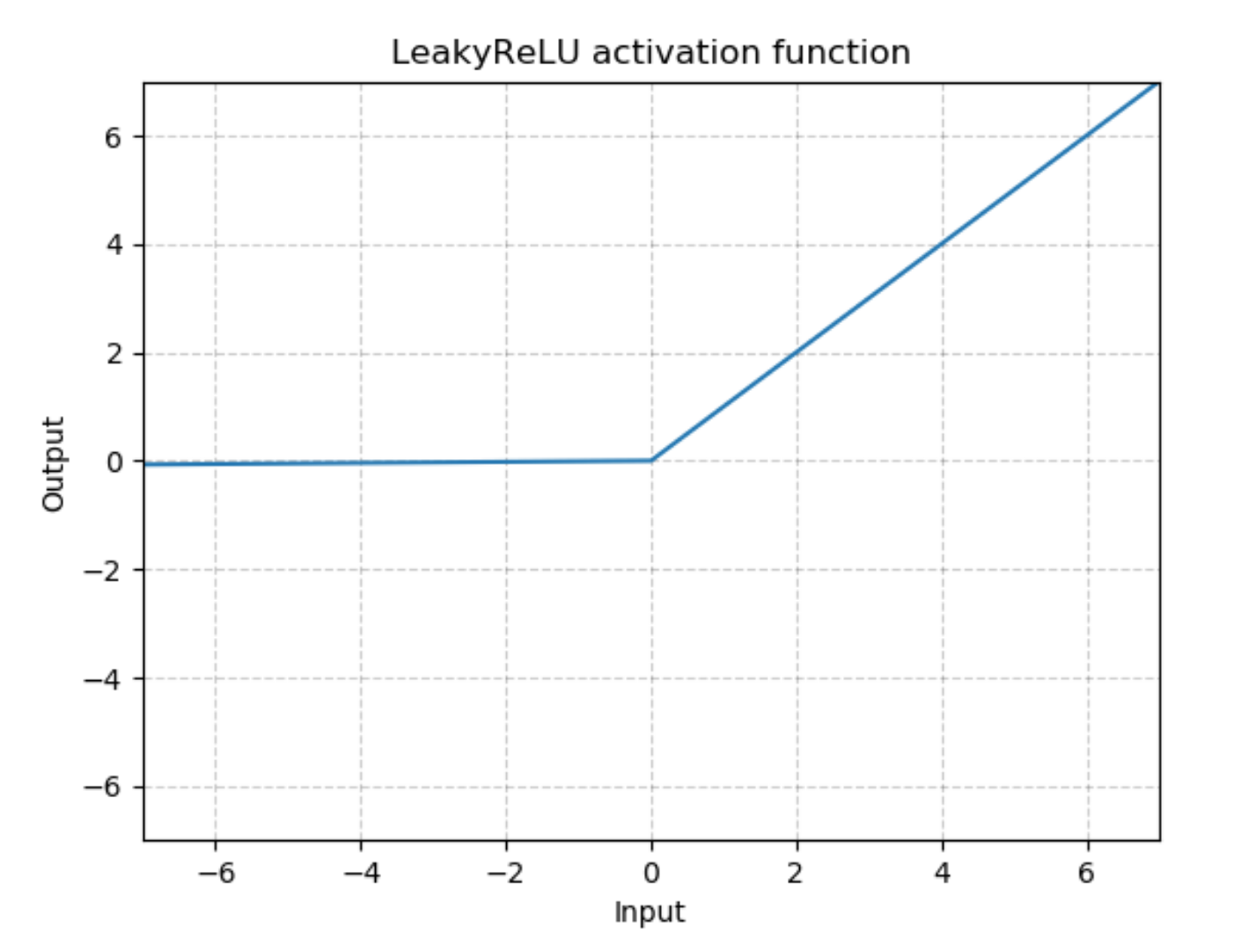
All hidden layers will have a Leaky ReLu activation function applied to their outputs.

Leaky ReLu

We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.

Sigmoid Output

We'll also take the approach of using a more numerically stable loss function on the outputs. Recall that we want the discriminator to output a value 0-1 indicating whether an image is real or fake.

We will ultimately use BCEWithLogitsLoss, which combines a sigmoid activation function and and binary cross entropy loss in one function.

So, our final output layer should not have any activation function applied to it.

Generator

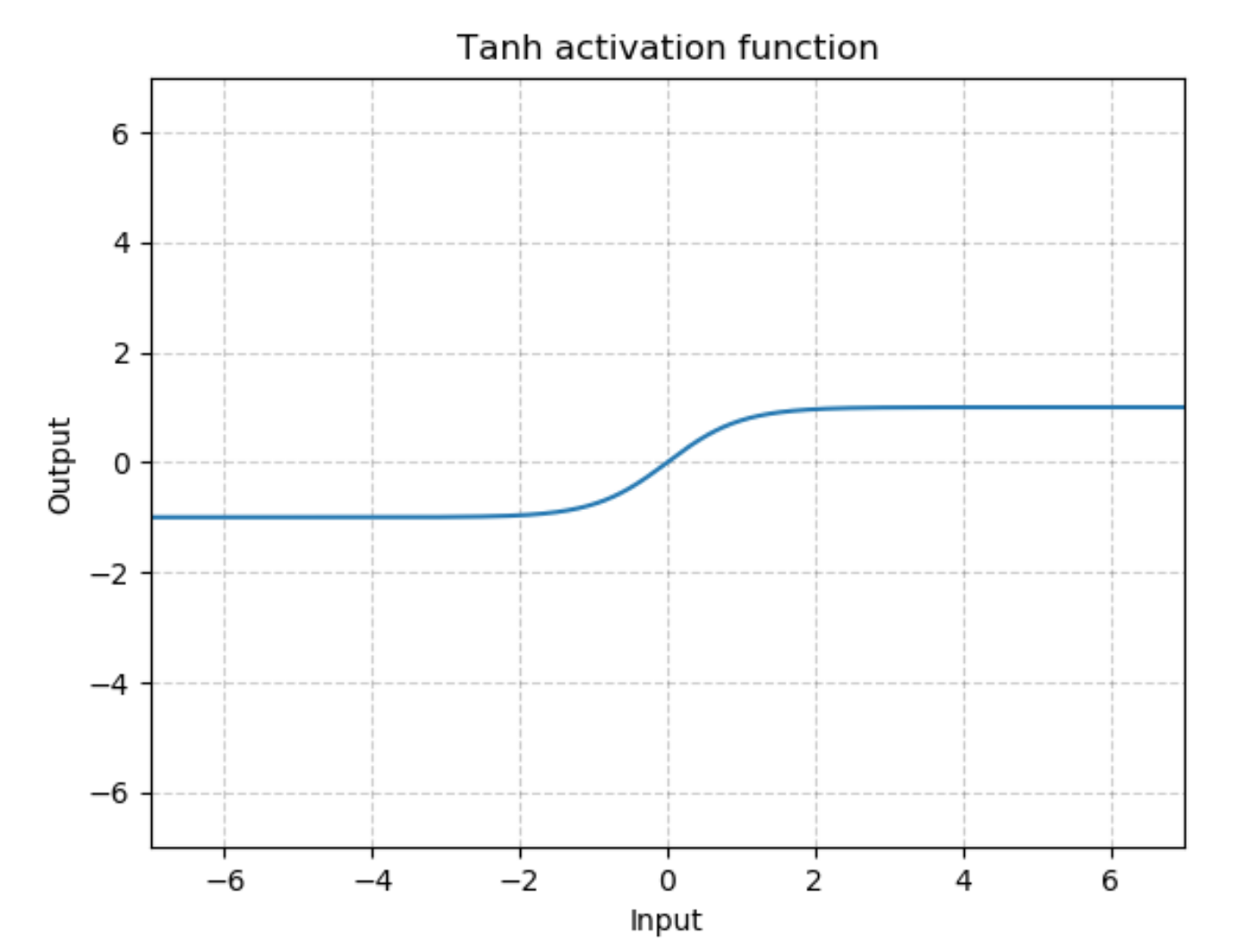
The generator network will be almost exactly the same as the discriminator network, except that we're applying a tanh activation function to our output layer.

tanh Output

The generator has been found to perform the best with $tanh$ for the generator output, which scales the output to be between -1 and 1, instead of 0 and 1.

Recall that we also want these outputs to be comparable to the real input pixel values, which are read in as normalized values between 0 and 1.

So, we'll also have to scale our real input images to have pixel values between -1 and 1 when we train the discriminator.