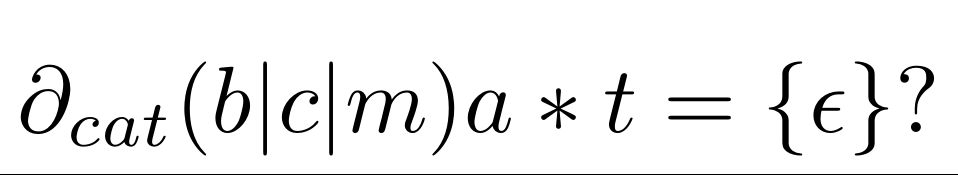This code is provided for educational purposes. It is not efficient. But it illustrates the idea.
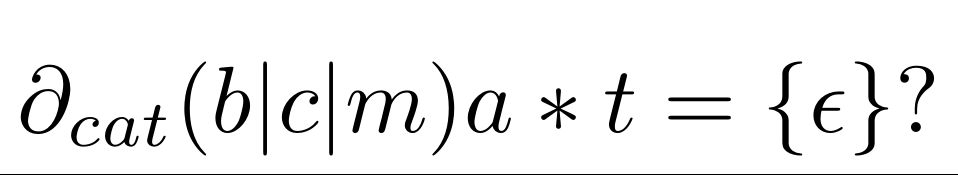
Brzozowski derivative is a less known technique to work with regular expressions. Normally, to match a string using regex we have to construct an automaton and simulate it. With the regex derivative technique we can use a regular expression 'directly' without the automaton construction and simulation.
It has nothing to do with classical derivative in analysis. But the symbolic nature and chain rule application make it feel similar. For more details there is a paper "Regular-expression derivative re-examined" by Scott Owens, John Reppy and Aaron Turon.
This code implements only three operators. There are concatenation ($\cdot$), alteration ($\mid$), and Kleene star($*$).
The usage is straightforward:
> python match.py <regex> <string>
E.g.
> python match.py '(c|b)at' 'cat'
(((c|b)·a)·t)
(((ϵ|∅)·a)·t)
((((∅|∅)·a)|ϵ)·t)
(((((∅|∅)·a)|∅)·t)|ϵ)
True
> python match.py '(c|b)at' 'sat'
(((c|b)·a)·t)
(((∅|∅)·a)·t)
(((∅|∅)·a)·t)
(((∅|∅)·a)·t)
False
The derivative of a language $L \subset \Sigma*$ with respect to a string $u \in \Sigma*$ is a language $\partial_u L = \lbrace v \mid u \cdot v \in L \rbrace$.
For any characters a and b and for any regular expressions r and s we have following rules:
$$
\begin{align}
\partial_a \varepsilon &= \emptyset & \\
\partial_a a &= \epsilon & \\
\partial_a b &= \emptyset & \text{ for }(a \neq b) \\
\partial_a (r \cdot s) &= \partial_a r \mid \nu(r) \cdot \partial_a s & \\
\partial_a (r \mid s) &= \partial_a r \mid \partial_a s & \\
\partial_a (r*) &= \partial_a r \cdot r* &
\end{align}
$$
where the function $\nu(r)$ checks if the language defined by regular expression contains an empty string ($\epsilon$). We call such regular expression nullable. The recursive definition of $\nu$ is:
$$
\begin{align}
\nu(\varepsilon) &= \varepsilon \\
\nu(\emptyset) &= \emptyset \\
\nu(a) &= \emptyset \\
\nu(r \cdot s) &= \nu(r) \cdot \nu(s) \\
\nu(r \mid s) &= \nu(r) \mid \nu(s) \\
\nu(r*) &= \varepsilon
\end{align}
$$
We need two rules with respect to strings to complete the rule set:
$$
\begin{align}
\partial_\varepsilon r &= r \\
\partial_{ua} &= \partial_{a} \partial_{u} r
\end{align}
$$
To find a match we have to check if the derivative of the regex $r$ with respect to string $u$ is nullable:
$$
\nu(\partial_{u} r) = \epsilon
$$
Let's check if word $cat$ matches the regexp $(c|b)at$. Obviously it is because the regex defines a language of just two strings $cat$ and $bat$. Anyway, let's do it formally.
$$
\partial_{cat}\left[(c \mid b)\cdot a \cdot t\right] = \partial_t\partial_a\partial_c\left[(c \mid b)\cdot a \cdot t\right]
$$
Let's take a derivative with respect of each character separately:
$$
\begin{align*}
\partial_c\left[(c \mid b)\cdot a \cdot t\right] &= \partial_c \left[c \mid b\right]\cdot a \cdot t \mid \nu(c \mid b) \cdot \partial_c [a \cdot t] & \text{ by } \cdot \text{-rule} \\
&= \partial_c \left[c \mid b\right]\cdot a \cdot t \mid \emptyset \cdot \partial_c [\cdot a \cdot t] & \nu(c \mid b) = \nu(c) \mid \nu(b) = \emptyset \mid \emptyset = \emptyset \\
&= \partial_c \left[c \mid b\right]\cdot a \cdot t \mid \emptyset & r \cdot \emptyset = \emptyset \cdot r = \emptyset \text{ for any }r \\
&= \partial_c \left[c \mid b\right]\cdot a \cdot t & r \mid \emptyset = \emptyset \mid r = r \text{ for any }r \\
&= (\partial_c c \mid \partial_c b) \cdot a \cdot t & \text{ by } \mid \text{-rule} \\
&= (\epsilon \mid \emptyset) \cdot a \cdot t & \\
&= \epsilon \cdot a \cdot t & \\
&= a \cdot t & \\
\partial_a[a \cdot t] &= \partial_a a \cdot t \mid \nu(a) \cdot \partial_a b & \text{ by } \cdot \text{-rule} \\
&= \epsilon \cdot t \mid \emptyset & \\
&= t & \\
\partial_t[t] &= \epsilon \\
\end{align*}
$$
So $\partial_{cat}\left[(c \mid b)\cdot a \cdot t\right] = \epsilon$ is nullable and the word $cat$ matches the regexp $(c \mid b)\cdot a \cdot t$.
- It is fun
- Using this technique we can construct a very efficient automaton called minimal DFA. There are some considerations though but in some cases such construction can be very handy.
- Extend the derivative theory section
- Add the DFA construction code