Implement a Planning Search

Synopsis

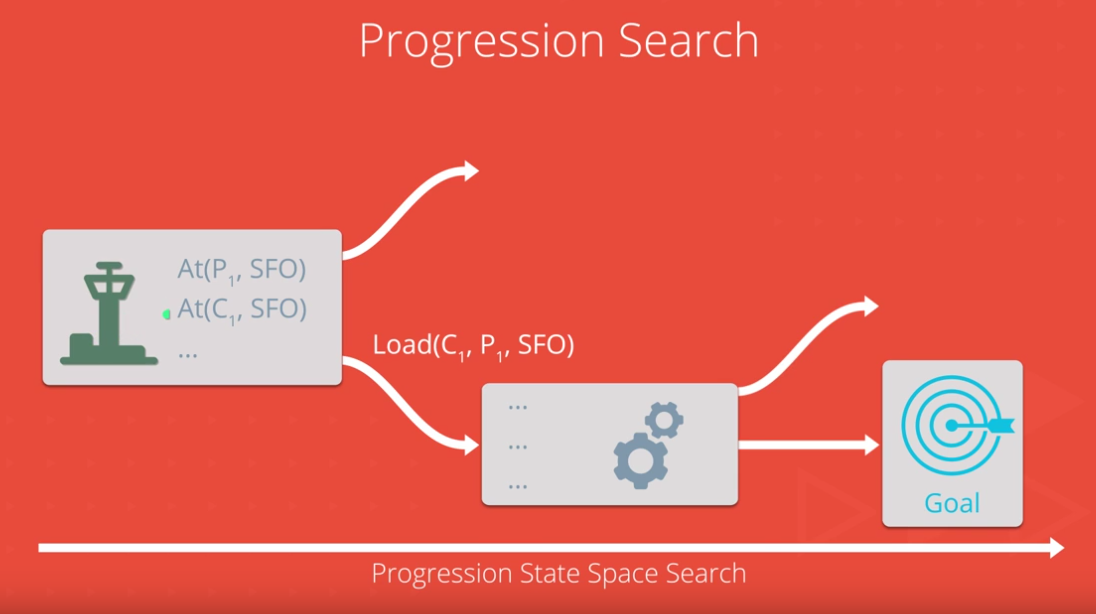
This project includes skeletons for the classes and functions needed to solve deterministic logistics planning problems for an Air Cargo transport system using a planning search agent. With progression search algorithms like those in the navigation problem from lecture, optimal plans for each problem will be computed. Unlike the navigation problem, there is no simple distance heuristic to aid the agent. Instead, you will implement domain-independent heuristics.

Part 1 - Planning problems:
- READ: applicable portions of the Russel/Norvig AIMA text
- GIVEN: problems defined in classical PDDL (Planning Domain Definition Language)
- TODO: Implement the Python methods and functions as marked in my_air_cargo_problems.py
- TODO: Experiment and document metrics
Part 2 - Domain-independent heuristics:
- READ: applicable portions of the Russel/Norvig AIMA text
- TODO: Implement relaxed problem heuristic in my_air_cargo_problems.py
- TODO: Implement Planning Graph and automatic heuristic in my_planning_graph.py
- TODO: Experiment and document metrics
Part 3 - Written Analysis

Environment requirements

Python 3.4 or higher
Starter code includes a copy of companion code for the Stuart Russel/Norvig AIMA text.

Project Details

Part 1 - Planning problems

READ: Stuart Russel and Peter Norvig text:

"Artificial Intelligence: A Modern Approach" 3rd edition chapter 10 or 2nd edition Chapter 11 on Planning, available on the AIMA book site sections:

The Planning Problem
Planning with State-space Search

GIVEN: classical PDDL problems

All problems are in the Air Cargo domain. They have the same action schema defined, but different initial states and goals.

Air Cargo Action Schema:

Action(Load(c, p, a),
	PRECOND: At(c, a) ∧ At(p, a) ∧ Cargo(c) ∧ Plane(p) ∧ Airport(a)
	EFFECT: ¬ At(c, a) ∧ In(c, p))
Action(Unload(c, p, a),
	PRECOND: In(c, p) ∧ At(p, a) ∧ Cargo(c) ∧ Plane(p) ∧ Airport(a)
	EFFECT: At(c, a) ∧ ¬ In(c, p))
Action(Fly(p, from, to),
	PRECOND: At(p, from) ∧ Plane(p) ∧ Airport(from) ∧ Airport(to)
	EFFECT: ¬ At(p, from) ∧ At(p, to))

Problem 1 initial state and goal:

Init(At(C1, SFO) ∧ At(C2, JFK) 
	∧ At(P1, SFO) ∧ At(P2, JFK) 
	∧ Cargo(C1) ∧ Cargo(C2) 
	∧ Plane(P1) ∧ Plane(P2)
	∧ Airport(JFK) ∧ Airport(SFO))
Goal(At(C1, JFK) ∧ At(C2, SFO))

Problem 2 initial state and goal:

Init(At(C1, SFO) ∧ At(C2, JFK) ∧ At(C3, ATL) 
	∧ At(P1, SFO) ∧ At(P2, JFK) ∧ At(P3, ATL) 
	∧ Cargo(C1) ∧ Cargo(C2) ∧ Cargo(C3)
	∧ Plane(P1) ∧ Plane(P2) ∧ Plane(P3)
	∧ Airport(JFK) ∧ Airport(SFO) ∧ Airport(ATL))
Goal(At(C1, JFK) ∧ At(C2, SFO) ∧ At(C3, SFO))

Problem 3 initial state and goal:

Init(At(C1, SFO) ∧ At(C2, JFK) ∧ At(C3, ATL) ∧ At(C4, ORD) 
	∧ At(P1, SFO) ∧ At(P2, JFK) 
	∧ Cargo(C1) ∧ Cargo(C2) ∧ Cargo(C3) ∧ Cargo(C4)
	∧ Plane(P1) ∧ Plane(P2)
	∧ Airport(JFK) ∧ Airport(SFO) ∧ Airport(ATL) ∧ Airport(ORD))
Goal(At(C1, JFK) ∧ At(C3, JFK) ∧ At(C2, SFO) ∧ At(C4, SFO))

TODO: Implement methods and functions in `my_air_cargo_problems.py`

AirCargoProblem.get_actions method including load_actions and unload_actions sub-functions
AirCargoProblem.actions method
AirCargoProblem.result method
air_cargo_p2 function
air_cargo_p3 function

TODO: Experiment and document metrics for non-heuristic planning solution searches

Run uninformed planning searches for air_cargo_p1, air_cargo_p2, and air_cargo_p3; provide metrics on number of node expansions required, number of goal tests, time elapsed, and optimality of solution for each search algorithm. Include the result of at least three of these searches, including breadth-first and depth-first, in your write-up (breadth_first_search and depth_first_graph_search).
If depth-first takes longer than 10 minutes for Problem 3 on your system, stop the search and provide this information in your report.
Use the run_search script for your data collection: from the command line type python run_search.py -h to learn more.

Why are we setting the problems up this way?

Progression planning problems can be solved with graph searches such as breadth-first, depth-first, and A*, where the nodes of the graph are "states" and edges are "actions". A "state" is the logical conjunction of all boolean ground "fluents", or state variables, that are possible for the problem using Propositional Logic. For example, we might have a problem to plan the transport of one cargo, C1, on a single available plane, P1, from one airport to another, SFO to JFK. In this simple example, there are five fluents, or state variables, which means our state space could be as large as . Note the following:

While the initial state defines every fluent explicitly, in this case mapped to TTFFF, the goal may be a set of states. Any state that is True for the fluent At(C1,JFK) meets the goal.

Even though PDDL uses variable to describe actions as "action schema", these problems are not solved with First Order Logic. They are solved with Propositional logic and must therefore be defined with concrete (non-variable) actions and literal (non-variable) fluents in state descriptions.

The fluents here are mapped to a simple string representing the boolean value of each fluent in the system, e.g. TTFFTT...TTF. This will be the state representation in the AirCargoProblem class and is compatible with the Node and Problem classes, and the search methods in the AIMA library.

Part 2 - Domain-independent heuristics

READ: Stuart Russel and Peter Norvig text

"Artificial Intelligence: A Modern Approach" 3rd edition chapter 10 or 2nd edition Chapter 11 on Planning, available on the AIMA book site section:

Planning Graph

TODO: Implement heuristic method in `my_air_cargo_problems.py`

AirCargoProblem.h_ignore_preconditions method

TODO: Implement a Planning Graph with automatic heuristics in `my_planning_graph.py`

PlanningGraph.add_action_level method
PlanningGraph.add_literal_level method
PlanningGraph.inconsistent_effects_mutex method
PlanningGraph.interference_mutex method
PlanningGraph.competing_needs_mutex method
PlanningGraph.negation_mutex method
PlanningGraph.inconsistent_support_mutex method
PlanningGraph.h_levelsum method

TODO: Experiment and document: metrics of A* searches with these heuristics

Run A* planning searches using the heuristics you have implemented on air_cargo_p1, air_cargo_p2 and air_cargo_p3. Provide metrics on number of node expansions required, number of goal tests, time elapsed, and optimality of solution for each search algorithm and include the results in your report.
Use the run_search script for this purpose: from the command line type python run_search.py -h to learn more.

Why a Planning Graph?

The planning graph is somewhat complex, but is useful in planning because it is a polynomial-size approximation of the exponential tree that represents all possible paths. The planning graph can be used to provide automated admissible heuristics for any domain. It can also be used as the first step in implementing GRAPHPLAN, a direct planning algorithm that you may wish to learn more about on your own (but we will not address it here).

Planning Graph example from the AIMA book

Part 3: Written Analysis

TODO: Include the following in your written analysis.

Provide an optimal plan for Problems 1, 2, and 3.
Compare and contrast non-heuristic search result metrics (optimality, time elapsed, number of node expansions) for Problems 1,2, and 3. Include breadth-first, depth-first, and at least one other uninformed non-heuristic search in your comparison; Your third choice of non-heuristic search may be skipped for Problem 3 if it takes longer than 10 minutes to run, but a note in this case should be included.
Compare and contrast heuristic search result metrics using A* with the "ignore preconditions" and "level-sum" heuristics for Problems 1, 2, and 3.
What was the best heuristic used in these problems? Was it better than non-heuristic search planning methods for all problems? Why or why not?
Provide tables or other visual aids as needed for clarity in your discussion.

Examples and Testing:

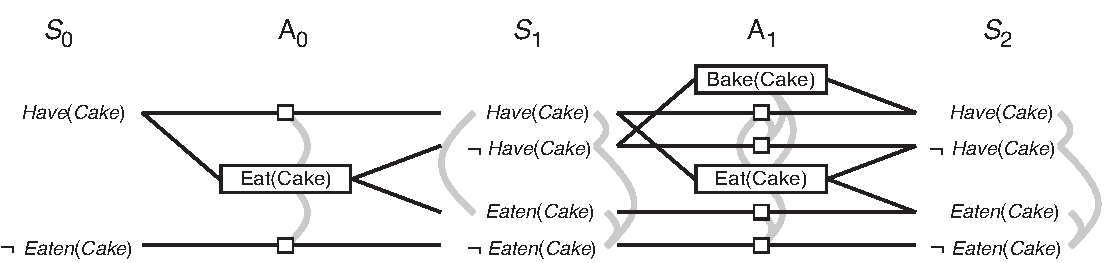
The planning problem for the "Have Cake and Eat it Too" problem in the book has been implemented in the example_have_cake module as an example.
The tests directory includes unittest test cases to evaluate your implementations. All tests should pass before you submit your project for . From the AIND-Planning directory command line:
- python -m unittest tests.test_my_air_cargo_problems
- python -m unittest tests.test_my_planning_graph
The run_search script is provided for gathering metrics for various search methods on any or all of the problems and should be used for this purpose.

kramea/AIND-Planning