Program Assignment #1

과제 개요

본 프로젝트는 2019학년도 1학기 컴파일러 실습 과제입니다.
주제: Infix representation을 postfix representation으로 변환합니다.

개발 환경

OS: Mac OS X 10.12.6 (Darwin Kernel Version 16.7.0)
Language: C
Compiler: clang (Apple LLVM version 9.0.0 (clang-900.0.39.2)), gmake (GNU Make 4.2.1)

빌드

Lex를 이용할 경우

$ lex -o lex.yy.c lexer.l
$ make

Lex를 이용하지 않을 경우

첨부된 lex.yy.c 파일을 이용하여 빌드합니다.

$ make

실행

만들어진 in2post 실행파일은 표준 입력으로 입력을 받고 표준 출력으로 파싱 결과를 출력합니다.

예시

$ echo "5 + -2" > input.txt
$ cat input.txt | ./in2post
5 -2 + 
$ echo "3 + a12-2 + 5" | ./in2post
3 a12 + 2 - 5 + 
$ echo "5abc0+102" | ./in2post
Error: Not an infix expression because:
	-> 5 is not an operator.

NOTE: 5abc0은 하나의 IDENTIFIER가 아닌 NUMBER와 IDENTIFIER로 분해됩니다.

프로그램 순서도

주요 함수

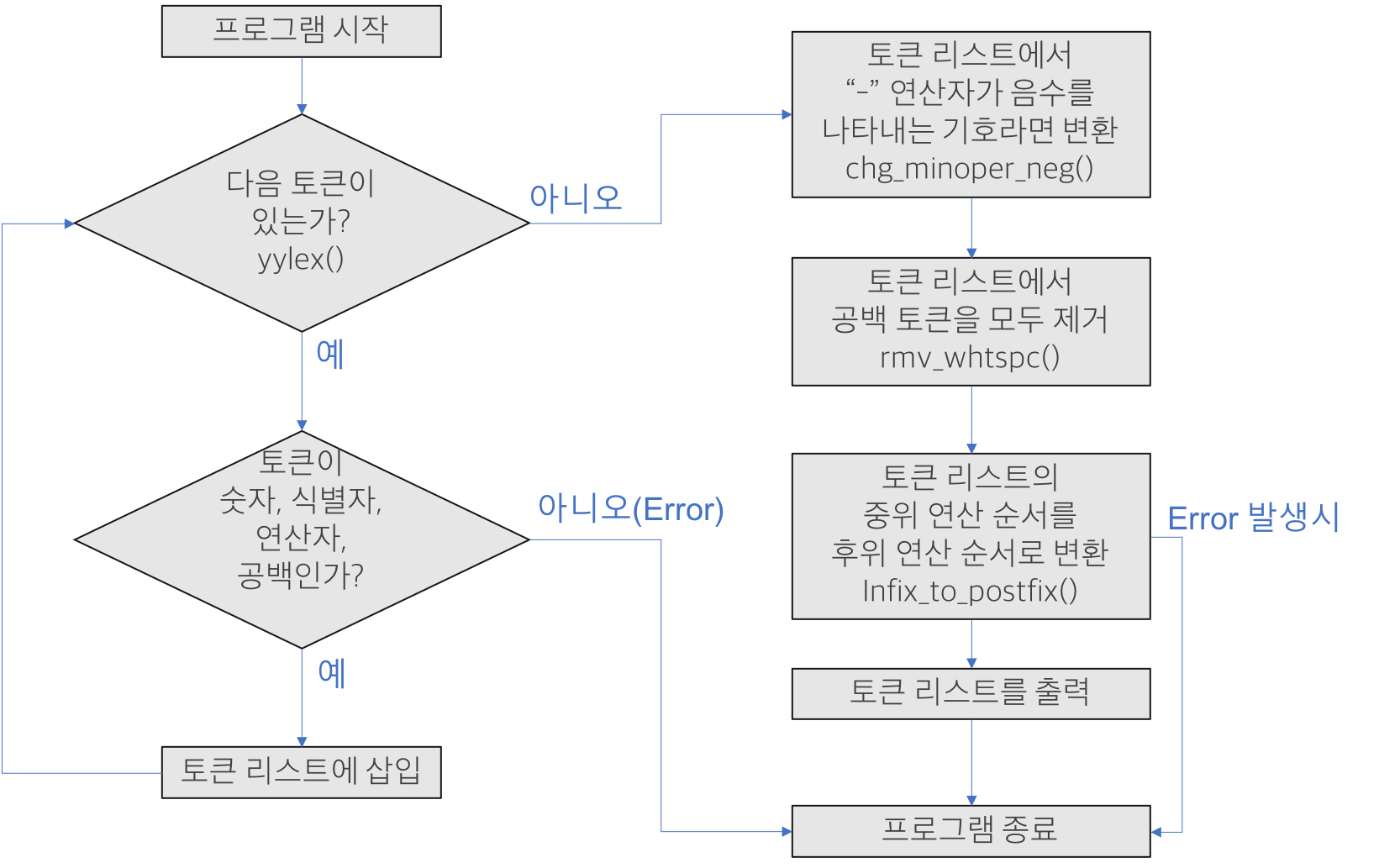
이 프로그램은 순서도에서 볼 수 있듯이 크게 네 가지 함수(yylex(), chg_minoper_neg(), rmv_whtspc(), infix_to_postfix()가 중요한 역할을 해냅니다. 그 중 yylex()는 lex에서 생성한 함수이므로 이에 대한 설명은 생략합니다. 아래는 나머지 세 함수에 대한 설명입니다.

void chg_minoper_neg(struct list_node *)

chg_minoper_neg()는 수식이 담긴 토큰 리스트를 받아 lex에서 "-" 연산자로 분류한 것 중 실제로는 음수를 나타내는 부호로서 사용된 토큰을 오른쪽에 있는 정수 토큰과 합쳐주는 작업을 수행합니다. 아이디어는 다음과 같습니다.

토큰 리스트를 순회하면서 빼기 연산자인지 확인한다.
어떤 토큰이 빼기 연산자일 경우, 왼쪽 토큰을 확인한다. (단, 왼쪽 토큰은 공백 토큰을 제외한 최초의 왼쪽 인접 토큰이다.) 이때,
- 왼쪽 토큰이 없으면서 오른쪽 토큰이 숫자라면 음수 부호다.
- 왼쪽 토큰이 연산자이면서 오른쪽 토큰이 숫자라면 음수 부호다.

void rmv_whtspc(struct list_node *)

rmv_whtspc()는 토큰 리스트에 있는 모든 공백 토큰을 제거합니다. yylex()를 순차적으로 수행할 때 공백 토큰을 토큰 리스트에 넣은 이유는 음수 부호 여부를 확실히 판단하기 위해서였습니다. 만약 5-- 3과 같은 입력이 들어올 때 공백 토큰이 토큰 리스트에 있지 않다면 프로그램은 오류 없이 5 -3 -라는 결과를 낼 것입니다. 그러나 공백 토큰이 토큰 리스트에 있었기에 사이에 공백이 있는 - 3는 음수로 분류 되지 않고 -연산자가 두 번 출현한 것으로 판단하고 안전하게 잘못된 수식을 판별할 수 있습니다.

chg_minoper_neg()가 호출된 이후에는 공백 토큰이 필요가 없어집니다. 그뿐만 아니라 후술할 infix_to_postfix()은 인자로 들어올 토큰 리스트에 공백이 없음을 전제로 합니다. 그러므로 rmv_whtspc()는 토큰 리스트를 순회하며 모든 공백 토큰을 제거해줄 필요가 있습니다.

struct list_node * infix_to_postfix(struct list_node *)

infix_to_postfix()는 과제의 핵심 요구조건, 바로 중위 연산 수식을 후위 연산 수식으로 바꾸어주는 역할을 수행합니다. 앞서 설명하였듯 인자로는 공백이 제거된 토큰 리스트만을 받기로 합니다.

이 함수는 재귀적인 전략을 사용합니다. 수식이 주어졌을 때 가장 오른쪽의 연산자와 우항은 순서를 바꾸고 좌항식은 재귀적으로 호출됩니다. 이를 Coq와 비슷한 스타일로 설명합니다.

먼저 +,- 밖에 없는 중위 연산 수식은 아래와 같이 귀납적으로 정의됩니다:

Inductive 중위 연산 수식 :=
    | 단항식
    | 중위 연산 수식 + 단항식
    | 중위 연산 수식 - 단항식.

그리고 이 함수의 전략은 아래와 같이 고정점을 정의함으로써 설명됩니다:

Fixpoint infix_to_postfix (수식) :=  
    match 수식 with
         | 단항식                           => 단항식
         | 중위 연산 수식(좌항식) + 단항식(우항)  => infix_to_postfix(좌항식) 우항 +
         | 중위 연산 수식(좌항식) - 단항식(우항)  => infix_to_postfix(좌항식) 우항 -
    end.

예를 들어, a + b + c는 (a + b) + c와 같은 패턴으로 인식되고 infix_to_postfix(a + b) c +로 evaluation됩니다.

이 함수는 중위 연산 수식 조건으로 인해 세 가지 오류로 인해 중도에 종료될 수 있습니다.

우항은 반드시 숫자이거나 식별자여야 한다. 그러나 연산자가 우항에 출현할 경우 오류다.
(단항식이 아닐 경우) 가운데 항은 반드시 연산자여야 한다. 그러나 연산자가 아닐 경우 오류다.
(단항식이 아닐 경우) 좌항식은 반드시 존재해야 한다. 그러나 없을 경우 오류다.

함수의 반환값은 기존에 주어진 리스트의 포인터가 됩니다.

NOTE: 각 함수의 세부적인 로직은 주석으로 기술되었습니다.

kyeongmincho/Homework__Compiler-1