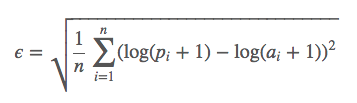Regression Case Study using kaggle's Farm Equipment Dataset
The goal of the exercise is to predict the sale price of a particular piece of heavy equipment at auction based on its usage, equipment type, and configuration. The data is sourced from auction result postings and includes information on usage and equipment configurations.
For the scope of this exercise, our class was limited to linear/regularized regression models, and it was completed as a four person team.
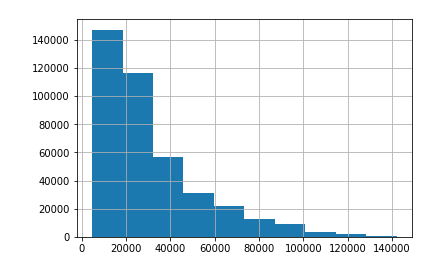
Sale Price is what we hope to predict with our regression model. After taking a quick look at a histogram of Sale Price, we can see it follows an exponential distribution.
This was a messy data set. To keep our model simple, we started by simply eliminating columns that contained null values (our simple model turned out to work great).
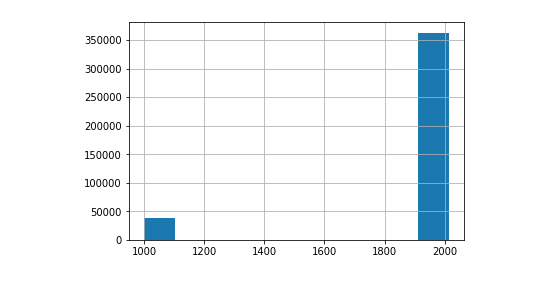
One important thing we noticed, was that Year Made was full of outliers. About 10% of the years were '1000' when in reality they should have been anywhere from the mid 1900s - early 2000s.
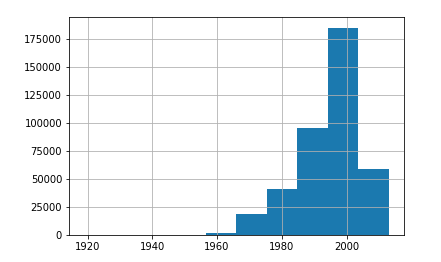
We could have dropped these, but getting rid of 10% of our data could be significant. We instead decided to replace these 1000s with the mode 'Year Made', which was 1998.
Great, our dataset is now ready to work with!
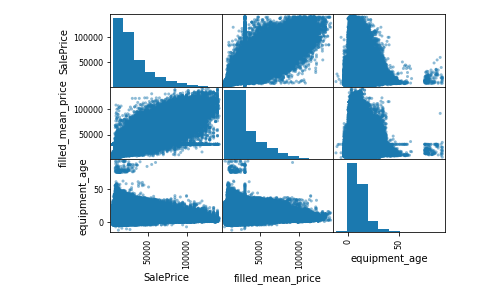
Using the data provided, we were able to create 2 new features, the 'Equipment Made' and 'Filled Mean Price'.
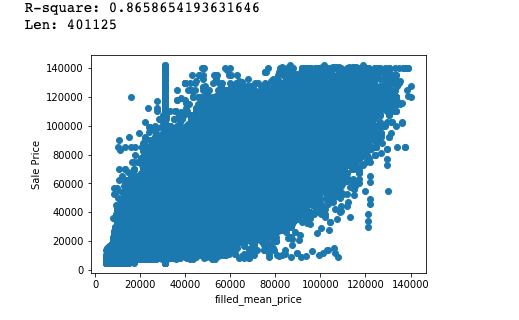
The 'Equipment Made' feature is simply the age of the Machine at the time of sale. 'Filled Mean Price' was more complicate to engineer. Using Pandas window functions, we were able to get the mean sale price for the past 5 sales of each Farm Equipment Model ID. This was very well correlated to the actual sale price, with an R-squared value of 0.87. Using a forward fill method, we were able to fill in any instances where there were not 5 past sales. Due to our good R-square value we were comfortable keeping our forward fill method in place.
Below is a scatter matrix of our engineered features
We evaluated our model with RMSLE
Using 10-Fold Cross Validation we were able to achieve a RMSLE score of below 0.35! Not bad for a linear regression model! (For comparison, good Random Forest Models tended to yield a better score of 0.22).