This repo contains my solutions to Algorithms, 4th edition 2-semester course by prof. Robert Sedgewick, Princeton University that I took in 2020.
Each directory is a standalone project whilst a lot of them might contain a couple of projects on a similar topic.
There is also a special folder called Algorithms that contains the fully formalised answers to each week's quizes, tests and projects, with explanations, colourful proofs, source code samples and the compiled binaries. It's divided into 2 folders for each semester:
Perfect matchings in k-regular bipartite graphs
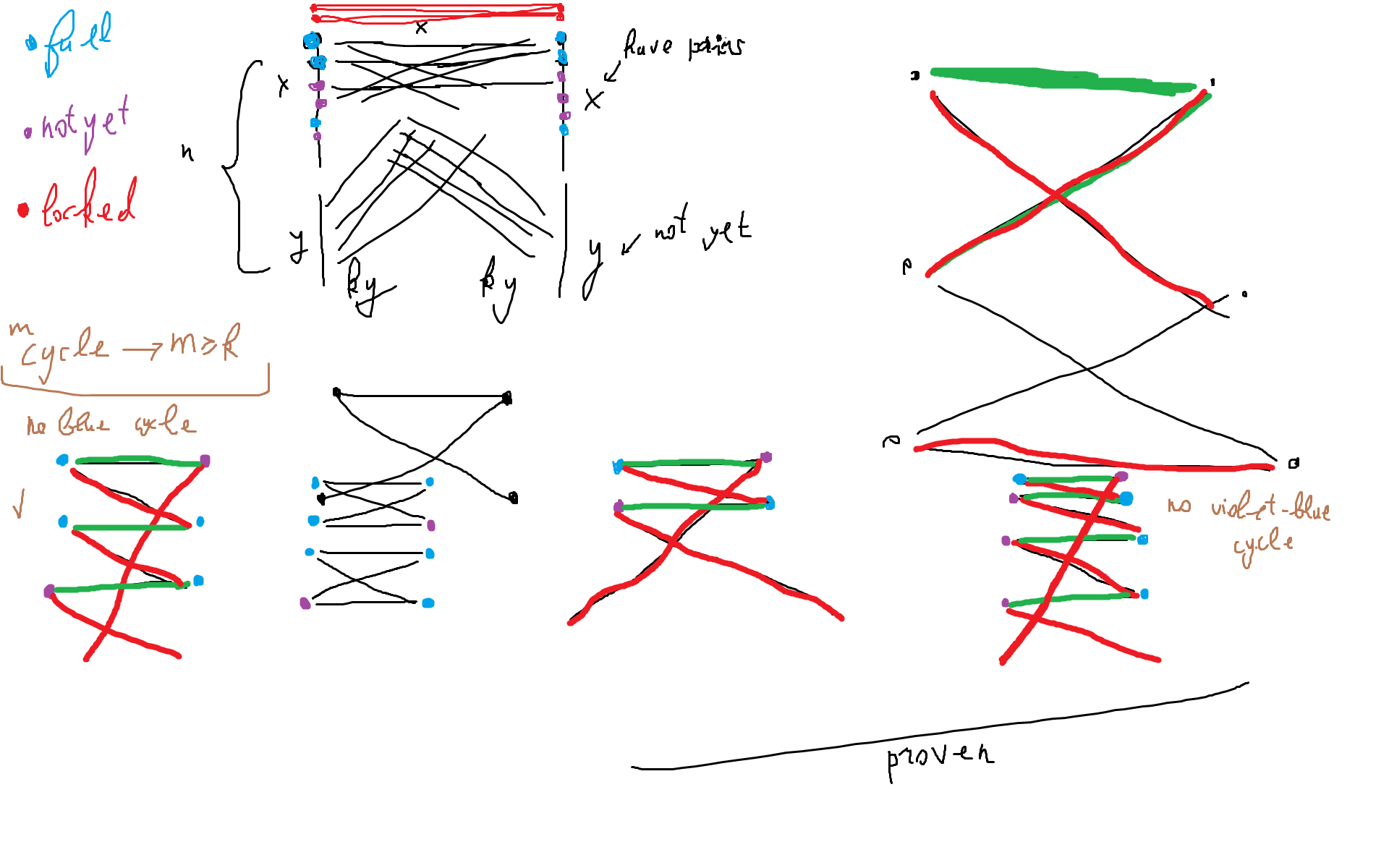
============================================================================================================
Formal proof:
1) Draw a bipartite graph with edges man-woman having infinite capacity, s-man and woman-t having capacity 1.
Use Ford-Fulkerson (FF). Let's call B-vertices those already connected to t (in maxflow) and A-vertices those
not yet connected.
2) At any stage finding a new augmenting path and the subsequent augmentation increases the value of a flow v
by 1. Since n is finite, then FF will terminate.
3) Now we have to prove, there will also be an augmentation path at any stage:
a) if a B-vertex is not connected somehow (locked) to some right (left) A-vertice,
then it can not be connected to some left (right) A-vertice, because: if one side is "locked"
then it has E edges pointing from it. Then another side has to have exactly E edges pointing from
it to the first side. No edges may point to any other vertice. One locked side requires another
side to being locked as well.
b) thus, a B-vertice where we get by a (right\left)A-B edge is unlocked and therefore it is connected
to another (left\right) A-vertice. And this way is an augmenting path.
c) if we get an A-A edge than it is already an augmenting path.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Undirected graph diameter search

All rights for the Java libraries and task ideas belong to their creators and Princeton University.