My solution of the IBM Ponder This challenge (organized by IBM Research in May 2017).
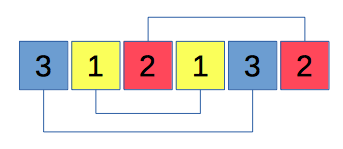
In the string CABACB, each letter appears exactly twice and the number of characters between the "A"s is one, between the "B"s is two, and between the "C"s is three.
The same problem with the letters A-E cannot be solved, but adding a space (in the form of a hyphen) allows it to be solved.
For example, in the string ADAEC-DBCEB, the number of characters between the "A"s is one, between the "B"s is two, between the "C"s is three (counting the space), between the "D"s is four, and between the "E"s is five.
Find a string of letters (A-Z) and "-" whose length is no more than 53 characters, where each of the 26 letters A-Z appears exactly twice, and there is one character between the "A"s, two between the "B"s ... and 26 between the "Z"s.
The URL of the web page with the problem description: http://www.research.ibm.com/haifa/ponderthis/challenges/May2017.html
It turns out, that the provided problem is a variation of the Langford pairing problem (from the area of combinatorial mathematics).
The Langford pairing sequence with n pairs can be constructed if and only if either 4 divides n, or 4 divides (n-3).
For characters "A-Z" amount of pairs of characters is n=26.
As far as 4 is neither a divisor of 26, nor a divisor of (26-3) - an extra space-character is required.
I have implemented a version of the Simulated Annealing algorithm for generation of the proper placement of the pairs of characters (according to the constraints of the problem).
The Java implementation of the described solution: SimulatedAnnealingSolution.java
In order to execute the solution it is just needed to run the method main of the class SimulatedAnnealingSolution.
Remark: of course this code is NOT of a production quality. The biggest accent is made on the succinct implementation of the described algorithm in combination with runtime and memory optimizations. Also, I was trying to use the meaningful names of the variables and functions, however sometimes it was not easy to came up with a proper naming.
Below is provided one of the possible answers, produced by my implementation:
Q-NDSTGYDZROFXGPENQFJVEUSWTOLRCJPYCKZMXBILBHVUAKAWIMH
Here is the list of possible placements, obtained via the Simulated Annealing solution for different amounts of pairs:
While I was solving the problem - I was feeling myself very involved, which encouraged me to investigate the properties of the Langford sequences from the probabilistic point of view.
Thus, I have written a blog post with all my findings: http://lagodiuk.github.io/computer_science/2017/06/04/langford_pairing_problem.html
Also, all my fidings are described in the PDF document: yurii_lahodiuk_may_2017_challenge.pdf