Self-Driving Car Engineer Nanodegree Program
The goal of this project is to steer a simulated car through a track using a PID controller.
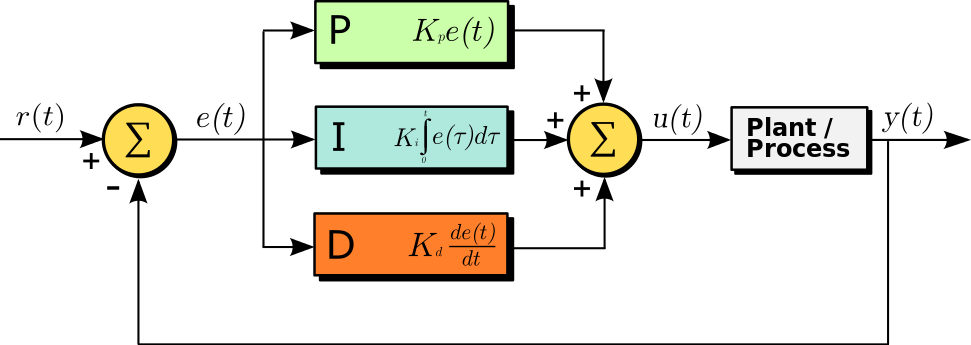
A PID (proportional, integral, derivative) controller is a control loop feedback mechanism. The PID controller calculates an error value e(t), the difference between the the desired and the measured value, and applies a correction that is a combination of the proportional (P), integral (I) and derivative (D) terms.
- Kp - proportianal coefficient
- Ki - integral coefficient
- Kd - differential coefficient
Variables:
- e(t) - error measurement at time t
- T - intedgration variable from time step [0..t]
The proportional term P is the difference between the desired and measured values, mutiplied by the proportianal coefficient Kd. If the output of the proportional term is too high, the system can become unstable. If it's too low, the rate of correction might be too slow and never reach the desired value.
The integral term I is a sum of all errors accumulated over time, multiplied by the integral coefficient Ki. The integral term can adjust for system bias.
The derivative term D is the error's rate of change, multiplied by the differential term Kd. The derivative term improves stability of the system.
My project uses the "twiddle** method for coefficient tuning. I have implemented the algorythm in a state machine to allow continuos tuning.
To avoid overfitting for certain parts of the track, each testing step drives the car about the whole length of the track and calculates the average error.
- for each coefficient
- set the inital value to P
- set the tuning range to D
- collect average error measurement E
- set E_best to E
- while tuning range > tolerance
- increase P by D
- collect average error measurement E
- if E < E_best
- set E_best to E
- multiply D by 1.1
- else
- decrease P by 2 * D
- collect average error measurement E
- if E < E_best
- set E_best to E
- multiply D by 1.1
- else
- increase P by D
- multiply D by 0.9