Fine-Grained-Blockchain-Rewriting-in-Permissionless-Setting

A construction of practical ABET scheme, in addition to a Proof-of-Work blockchain implemented. The ABET scheme can be used to secure blockchain rewriting, such that trapdoor holder may maliciously rewrite the blockchain without being identified.

A video for demo can be found at this(with subtitles) and this(without subtitles).

The full version of our paper can be found in the paper/ folder.

Prerequisites

The schemes have been tested with Python 3.6.7 on Mac OS X. First, verify that you have installed the following dependencies:

GMP 5.x
PBC library
Charm 0.43, this can be installed from this page
OpenSSL

Overview

The instantiation includes the following primitives: an attribute-based encryption KP-ABE, a hierarch identity-based encryption HIBE, a chameleon hash with ephemeral trapdoor, a digital signature scheme (e.g., Schnorr), a DPSS protocol and a running Proof-of-Work blockchain.

Some basic details of the implementation are:

scheme.py: full code of setup(), keygen(), hash(), verify(), adapt() algorithms
sharing.py: code of DPSS protocol 
blockchain/: code of blockchain with nodes

Instructions to run

Clone the project,

$ git clone https://github.com/lbwtorino/Fine-Grained-Blockchain-Rewriting-in-Permissionless-Setting.git

Once installed all the dependencies, to run and test ABET scheme,

$ python main.py ABET

The ABET logic is from scheme.py, including Setup(), KeyGen(), Hash(),Verify() and Adapt() functions. We provide an output file (the output data objects are referred to Section 5.2 of our paper) in ABET.txt.

You can also seperately run and test DPSS protocol, make sure your python installed fractions package,

$ python main.py DPSS

The DPSS logic is from sharing.py. In the test case, we provide the data shared between old committees and new committees (both size includes 5 committee members). We provide an execution output example in ./DPSS.txt, where

Secret is Secret (in our scenria, Secret is msk['alpha']), The shares to Committee A indicates the Committee A (old committee)'s shares (in this demo, it contains 5 shares and each of them is distributed to every member in Committee A),
The shares from Committee A to Committee B: denotes the re-shares that should be distributed from Committee A to new Committee B (as size of Committee B is 5, every Committee A re-calculate its shares into 5 slices, each slice is distributed to each Committee B member),
The new shares in Committee B: refers to the shares that Committee B re-calculate after receiving shares from Committee A (obviously, each Committee B member will receive 5 slices from 5 Committee A members. Then, for each Committee B member, he use Shamir's recovery algorithm to calculate a value. This value is the new share for himself),
recovered_Secret means the recovered secret from new Committee B. As shown, recovered_Secret is equal to Secret.

Deploy a blockchain and nodes

Install the dependencies: install merklelib if your python environment doesn't have before

$ cd blockchain/
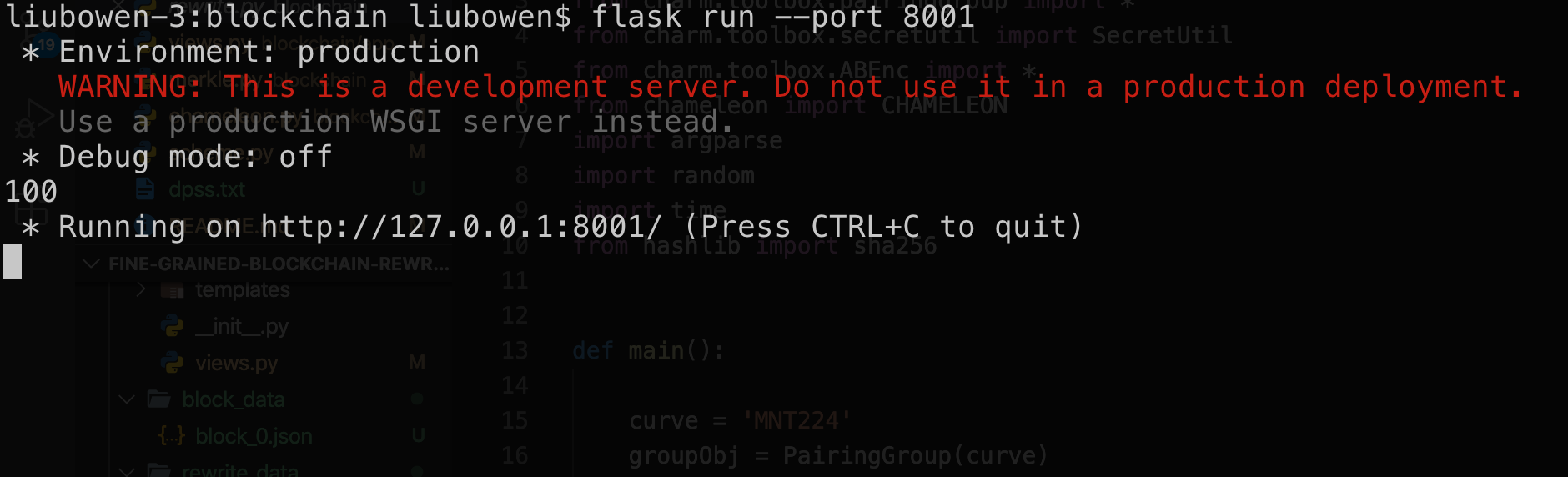
$ pip install -r requirements.txt

Start a blockchain, the port number is set to 8001,

$ export FLASK_APP=node_server.py
$ flask run --port 8001

As shown below, one instance of our blockchain is now up and running at port 8001.

To play around multiple custom nodes, run the blockchain on a different terminal session, here's a sample scenario that you might wanna try.

$ flask run --port 8005
$ flask run --port 8006
$ flask run --port 8007
......

As shown below, now we are deploying three nodes on blockchain.

Interact with blockchain

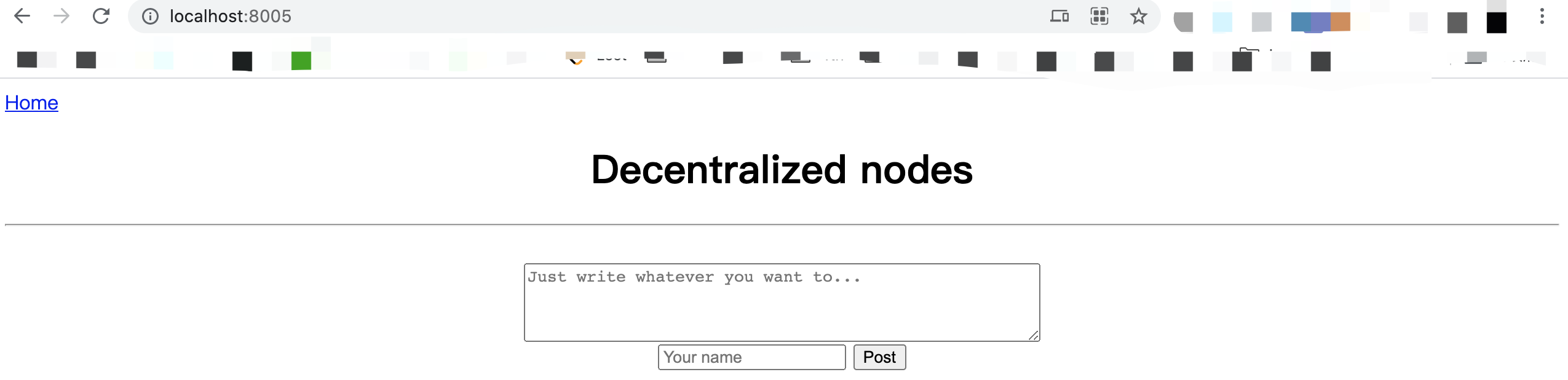
Every node interacts with blockchain by sending transaction via http://localhost:{port_number}. In your browser, type http://localhost:{port_number} (e.g., http://localhost:8005/). The UI of each node is shown below:

To send a transaction to blockchain, type the data and your id and by clicking Post button.

To mine the transaction, in your browser, type http://localhost:8001/mine.

In our construction, each transaction contains the following properties (a json format):

"author": transaction creator,
"content": post_content,
"tx_hash": the hashed value (traditional blockchain generates this field by generic SHA256 hash function while we propose a chameleon hash function that allows to change the content but keep the chameleon hash value unchanged to achieve rewrite blockchain),
"timestamp": time

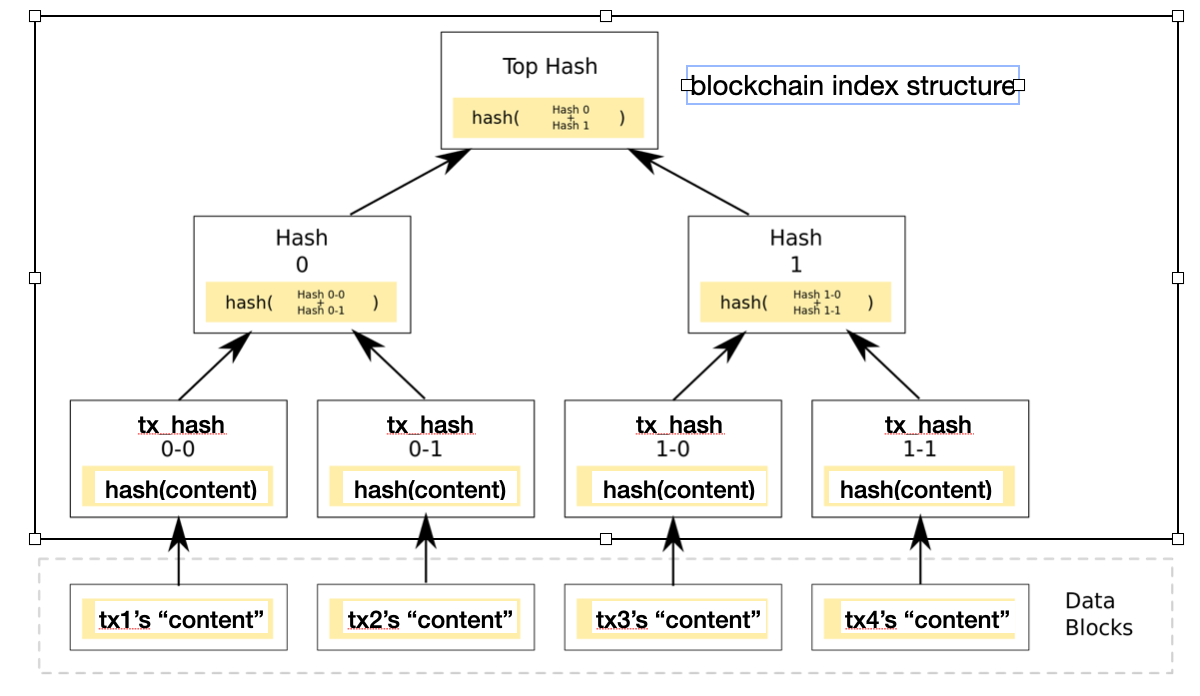
[Objective]: Please note that in the upper-layer real-worl blockchain (Merkle tree structure) only saves the tx_hash not content itself (as shown below). This is actually the objective of our paper. In traditional blockchain tx_hash (i.e., H(content)), H() refers to SHA256.

In our paper, H() denotes the chameleon hash function we proposed, which allows m and m' (different message) to have identical hash value. Thus, malicious/curious/authorized roles are able to rewrite the blockchain (i.e., the content can be changed from m to m' but tx_hash is unchanged)

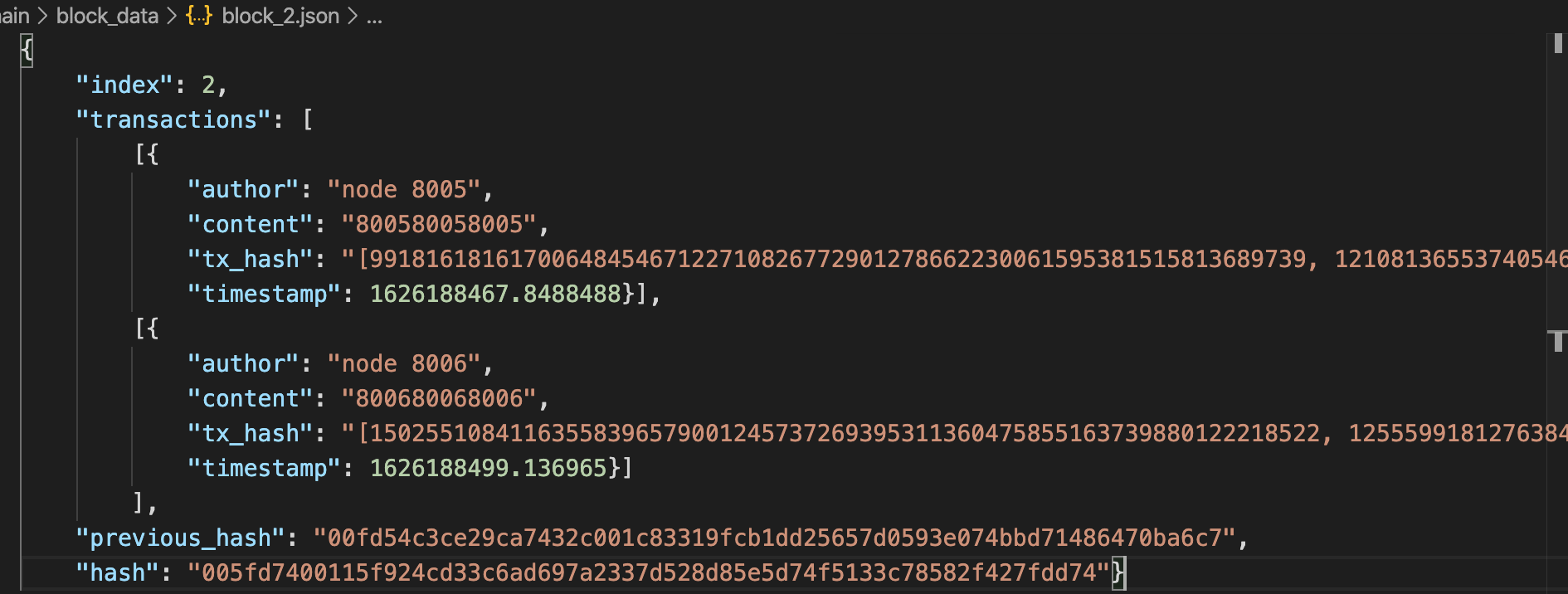
The chain data (transaction details) are saved in ./block_data. As shown below, we give an example with two mined transactions. Please pay attention to the and tx_hash, we may introduce how to rewrite blockchain in the next section.

Rewrite blockchain

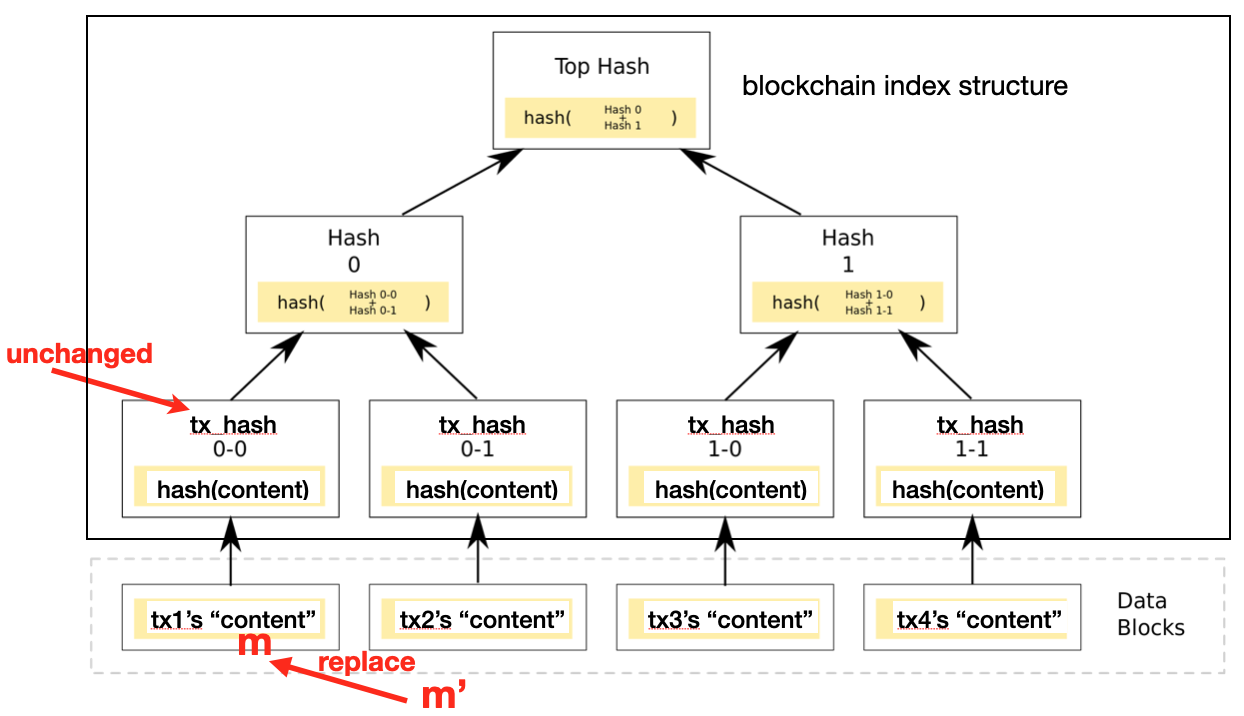
In traditional blockchain constructions tx_hash (i.e., H(content)), H() represents SHA-256, where m and m' have different hash value (collision-resistance property). In contrast, in our paper H() is a new chameleon hash we proposed that allows m and m' are able to have the same hash value by performing specific strategy (refers to Section 5.2 Adapt() method).

By doing so, malicious/curious/authorized roles are able to rewrite the blockchain, as low-layer storage m can be replaced by m' but tx_hash (stored at upper-layer blockchain's Merkle tree) is unchanged.

We demonstrate how to rewrite each transaction in ./rewrite_data. Each file contains the required data for each transaction hash. In previous section, the two transaction hash are

[9918161816170064845467122710826772901278662230061595381515813689739, 12108136553740546721779993929916482825396745683250111126990696946019]

and [15025510841163558396579001245737269395311360475855163739880122218522, 1255599181276384280583862572561718270445146402237492801822382134568].

Please note that the chameleon hash values take the format of 2-element array(shown above)

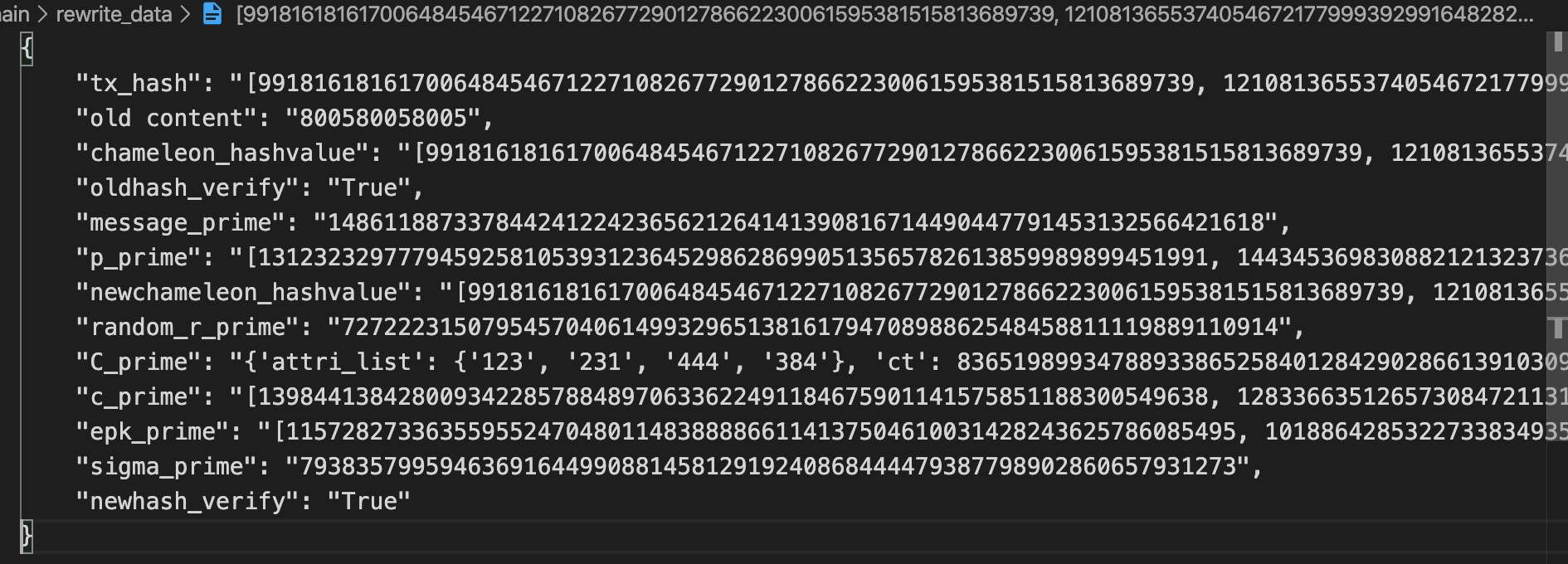
The example for such two transaction in ./rewrite_data. Taking 1st transaction as an example (please also refer to Section 5.2 of our paper), where

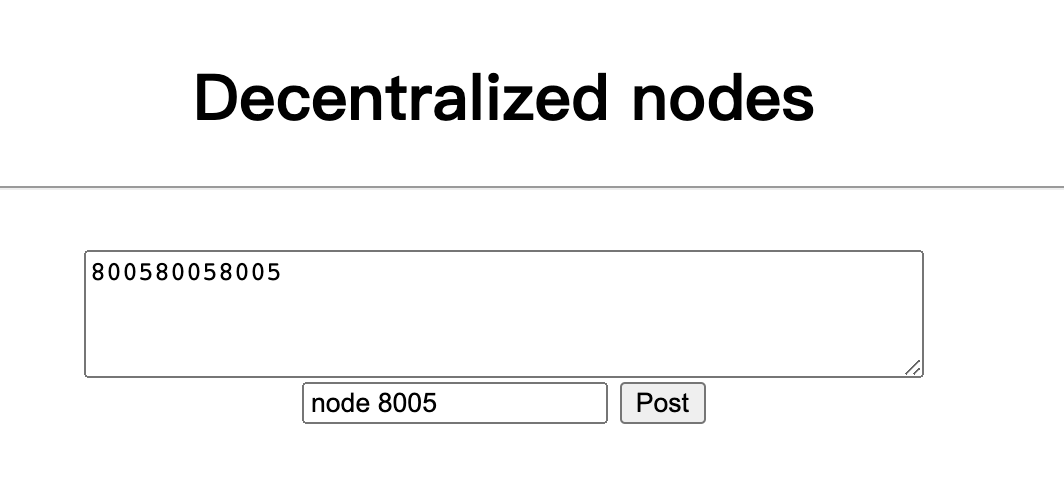
old content is the posted content by node 8005,
chameleon_hashvalue equals to tx_hash computed by our proposed chameleon hash function,
(message_prime, p_prime, newchameleon_hashvalue, random_r_prime, C_prime, c_prime, epk_prime, sigma_prime) are the required data to rewrite blockchain. (You may find details in Adapt() of Section 5.2 of our paper).
newhash_verify is the Verify() result.

Please find the process of cryptography correctness in our paper. Generally speaking, you can find that

message m is from 800580058005 to m' 1486118873378442412242365621264141390816714490447791453132566421618, but chameleon_hashvalue and newchameleon_hashvalue are same (actually, they are equal to tx_hash)
newhash_verify is True. This value is obtained by executing Verify() method, indicating the replacement (rewrite) is corret.