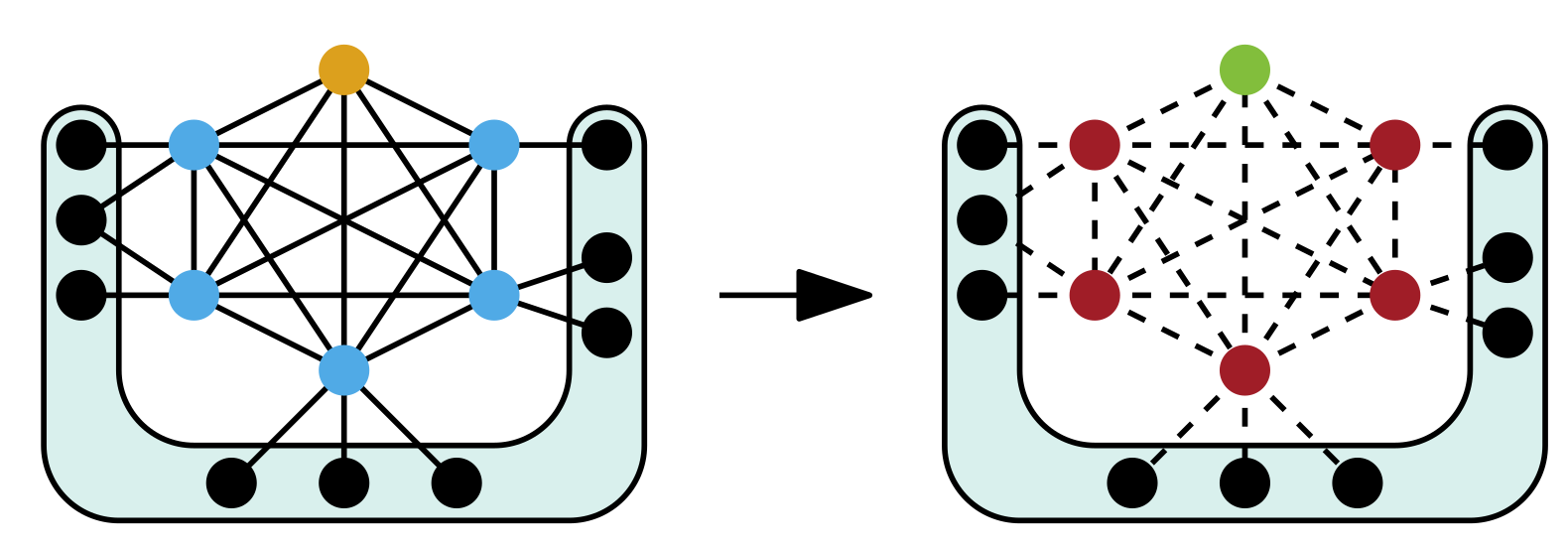
This is the open source project KaMIS - Karlsruhe Maximum Independent Sets. Given a graph G=(V,E), the goal of the maximum independent set problem is to compute a maximum cardinality set of vertices I, such that no vertices in the set are adjacent to one another. Such a set is called a maximum independent set. The problem is NP-hard and particularly difficult to solve in large sparse graphs.
Main project site: http://KarlsruheMIS.github.io
Compile the source by running compile_withcmake.sh. The binaries can then be found in the folder deploy. To compile the programs you need g++, OpenMP and cmake installed.
To convert a graph from DIMACS to METIS format or sort its edges you can use the python scripts in the misc folder.
The version of our framework currently contains the following algorithms:
- redumis -- run an evolutionary algorithm on a reduced graph
- onlinemis -- local search pruned with reductions
- weighted_branch_reduce -- a branch and reduce algorithm for weighed maximum independent sets
- weighted_local_search -- a local search algorithm for weighed maximum independent sets
- If you want to use the solver that one the vertex cover track of the PACE Challenge, go here https://github.com/KarlsruheMIS/pace-2019
Furthermore, the framework contains tools to make life a little bit easier:
- sort_adjacencies -- takes a graph file and sorts the neighborhoods of vertices (this is required by our algorithms)
- graphchecker -- check if the graph file you gave to algorithm is in the correct format
redumis FILE [options].
This is a brief overview of the most important options. For a full description, please take a look at the user guide.
FILE
Path to graph file that you want the maximum independent set for.
--help
Print help.
--console_log
Write the log to the console.
--output=<string>
Path to store the resulting independent set.
--seed=<int>
Seed to use for the random number generator.
--config=<string>
Config to use for the evolutionary algorithm [standard|social].
--time_limit=<double>
Time limit until the algorithm terminates.
online_mis FILE [options].
This is a brief overview of the most important options. For a full description, please take a look at the user guide.
FILE
Path to graph file that you want the maximum independent set for.
--help
Print help.
--console_log
Write the log to the console.
--output=<string>
Path to store the resulting independent set.
--seed=<int>
Seed to use for the random number generator.
--time_limit=<double>
Time limit until the algorithm terminates.
--adaptive_greedy
Use adaptive greedy solution
weighted_branch_reduce FILE [options].
weighted_local_search FILE [options].
This is a brief overview of the most important options. For a full description, please take a look at the user guide.
FILE
Path to graph file that you want the maximum independent set for.
--help
Print help.
--console_log
Write the log to the console.
--output=<string>
Path to store the resulting independent set.
--seed=<int>
Seed to use for the random number generator.
--time_limit=<double>
Time limit until the algorithm terminates.
--weight_source=<string>
Choose how the weights are assigned. Can be either: file (default), hybrid, uniform, geometric.
--reduction_style=<string>
Choose the type of reductions appropriate for the input graph. Can be either: normal/sparse (default), dense/osm.
sort_adjacencies FILE.
The program reads a Metis file, sorts the neighborhood of each node and prints the graph to the console.
graphchecker FILE.
The program reads a Metis file and checks the file for correctness.
The project is released under MIT. However, some files used for kernelization are released under the BSD 3-clause license. See the respective files for their license. If you publish results using our algorithms, please acknowledge our work by quoting one or more of the following papers:
@article{DBLP:journals/heuristics/LammSSSW17,
author = {Sebastian Lamm and
Peter Sanders and
Christian Schulz and
Darren Strash and
Renato F. Werneck},
title = {Finding near-optimal independent sets at scale},
journal = {J. Heuristics},
volume = {23},
number = {4},
pages = {207--229},
year = {2017},
url = {https://doi.org/10.1007/s10732-017-9337-x},
doi = {10.1007/s10732-017-9337-x},
timestamp = {Fri, 27 Dec 2019 21:13:52 +0100},
biburl = {https://dblp.org/rec/journals/heuristics/LammSSSW17.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
If you use fast kernelization routines (note that this is the default), the please also cite the following:
@article{DBLP:journals/jea/Hespe0S19,
author = {Demian Hespe and
Christian Schulz and
Darren Strash},
title = {Scalable Kernelization for Maximum Independent Sets},
journal = {{ACM} Journal of Experimental Algorithmics},
volume = {24},
number = {1},
pages = {1.16:1--1.16:22},
year = {2019},
url = {https://doi.org/10.1145/3355502},
doi = {10.1145/3355502},
timestamp = {Fri, 27 Mar 2020 08:38:35 +0100},
biburl = {https://dblp.org/rec/journals/jea/Hespe0S19.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
If you use OnlineMIS, then please also cite the following:
@inproceedings{DBLP:conf/wea/DahlumLS0SW16,
author = {Jakob Dahlum and
Sebastian Lamm and
Peter Sanders and
Christian Schulz and
Darren Strash and
Renato F. Werneck},
title = {Accelerating Local Search for the Maximum Independent Set Problem},
booktitle = {15th International Symposium on Experimental Algorithms {SEA}},
pages = {118--133},
year = {2016},
series = {Lecture Notes in Computer Science},
volume = {9685},
publisher = {Springer},
url = {https://doi.org/10.1007/978-3-319-38851-9\_9}
}
If you use the weighted independents set algorithms, please also cite the following:
@inproceedings{DBLP:conf/alenex/Lamm0SWZ19,
author = {Sebastian Lamm and
Christian Schulz and
Darren Strash and
Robert Williger and
Huashuo Zhang},
title = {Exactly Solving the Maximum Weight Independent Set Problem on Large Real-World Graphs},
booktitle = {Proceedings of the Twenty-First Workshop on Algorithm Engineering and Experiments, {ALENEX} 2019},
pages = {144--158},
year = {2019},
url = {https://doi.org/10.1137/1.9781611975499.12},
doi = {10.1137/1.9781611975499.12},
publisher = {{SIAM}},
year = {2019}
}