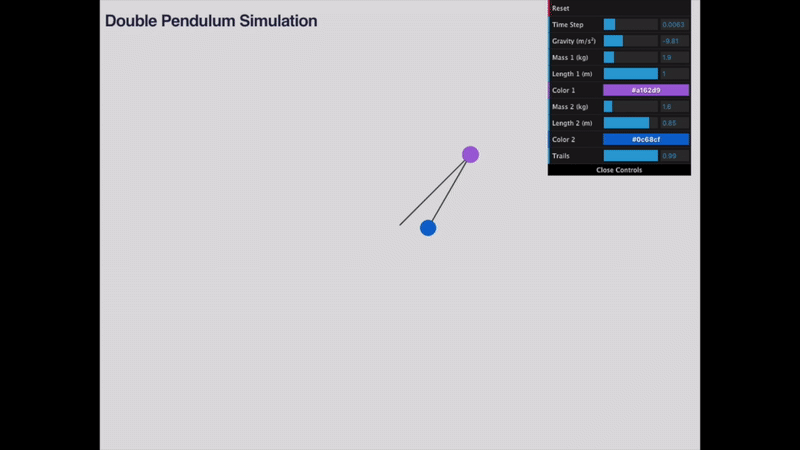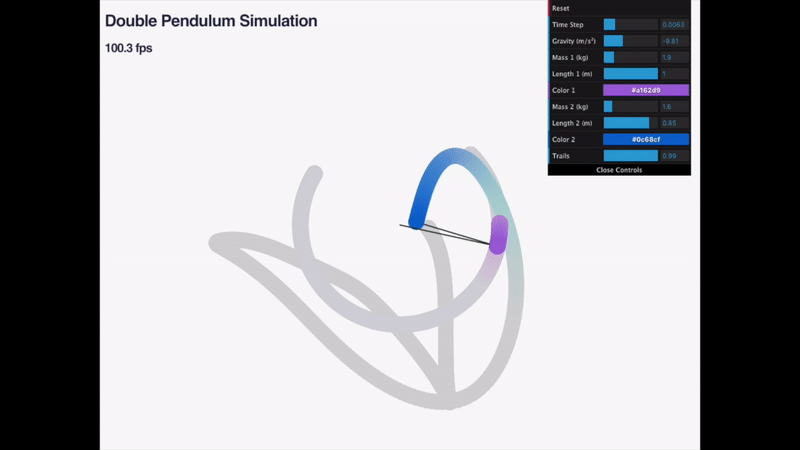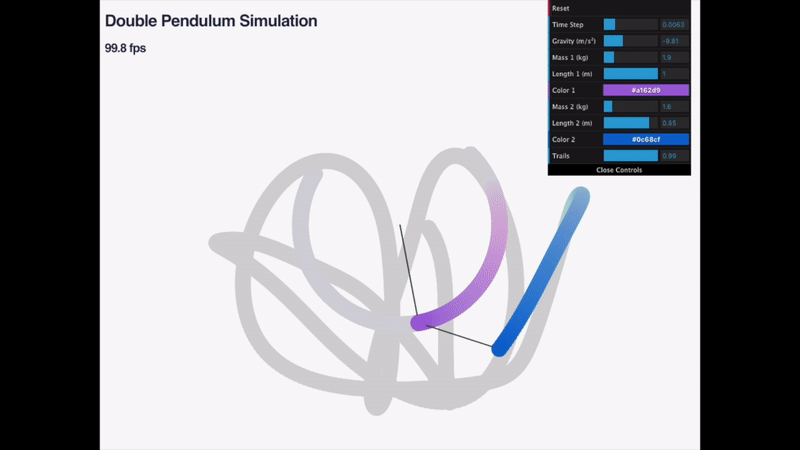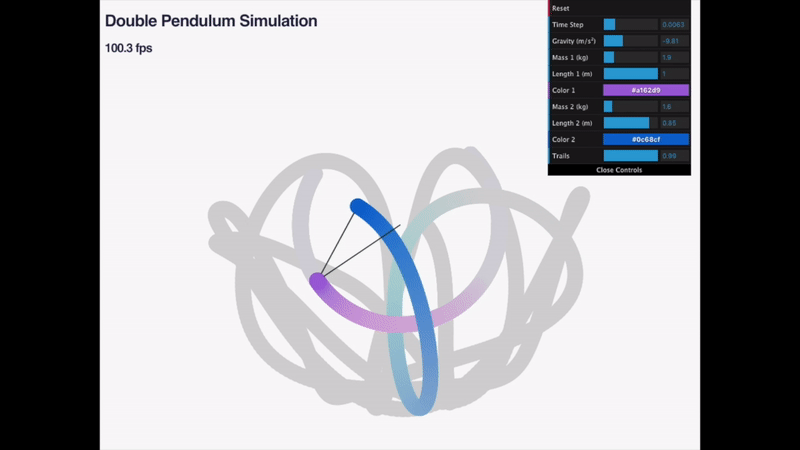
Simulation of a double pendulum written in ECMA script.
git clone git@github.com:lemmingapex/double-pendulum.git && cd double-pendulumnpm installnpm run build- open ./dist/index.html in google chrome.
This simulation attempts to semi-accurately represent the motion of a double pendulum.
The equations of motion can be found directly from the equations describing the kinematics and dynamics of the system.
Using equation [11] & [12] and [1], [2], [3] & [4], two explicit equations for the angular acceleration, θ₁′′ and θ₂′′, can expressed. I used mathics, a free CAS (computer algebra system), to do the algebra for me:
eq1 = x1pp==-1*L1*Sin[t1]*t1p^2 + L1*Cos[t1]*t1pp
eq2 = y1pp == L1*Cos[t1]*t1p^2 + L1*Sin[t1]*t1pp
eq3 = x2pp == x1pp - L2*Sin[t2]*t2p^2 + L2*Cos[t2]*t2pp
eq4 = y2pp == y1pp + L2*Cos[t2]*t2p^2 + L2*Sin[t2]*t2pp
eq11 = -Cos[t1]*(m1*x1pp + m2*x2pp) == Sin[t1]*(m1*y1pp + m2*y2pp + m2*g + m1*g)
eq12 = -m2*x2pp*Cos[t2] == Sin[t2]*(m2*y2pp + m2*g)
Solve[{eq1, eq3, eq2, eq4, eq11, eq12}, {t2pp, t1pp, x1pp, y1pp, x2pp, y2pp}]
The equations for t1pp and t2pp above are the equations of motion of interest.
In order to get the semi-accurate behavior, I am using an explicit RK4 integration method to solve the ODEs. Implicit methods would be preferred, but I am lazy and did not pursue this approach.
The chaotic behavior of the trajectory of the second mass at large angles of theta is pretty interesting.
- Make the simulation more interactive.
- Triple pendulum system?
- Inverted pendulums?