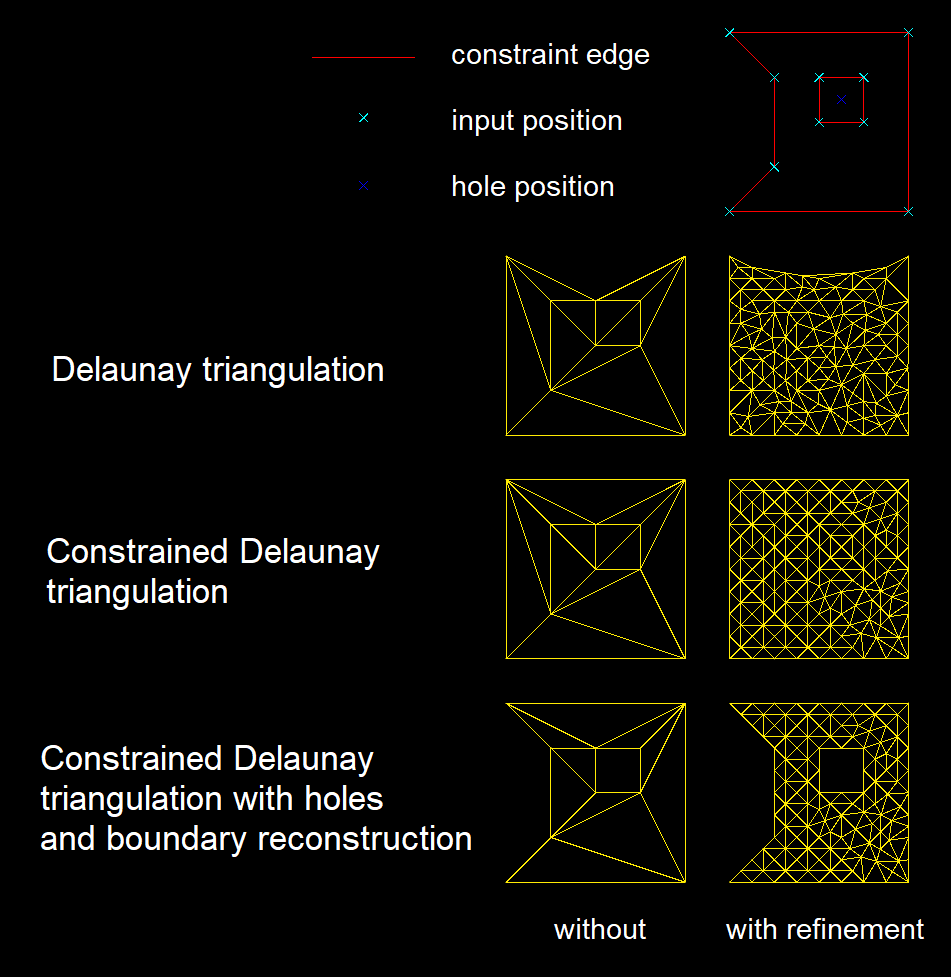
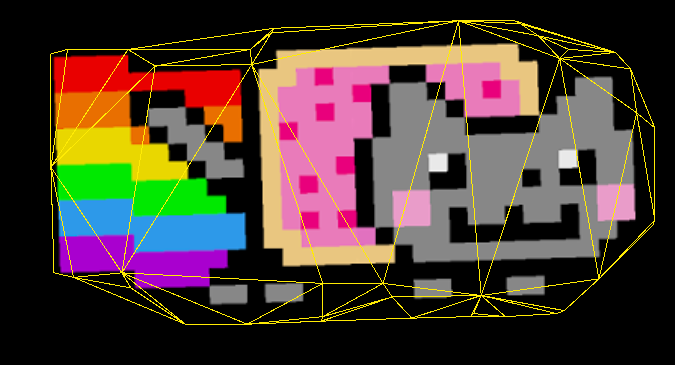/BurstTriangulator

2d Delaunay triangulation with mesh refinement for Unity with Burst compiler

Primary LanguageC#MIT LicenseMIT

Burst Triangulator

logo-light-mode logo-dark-mode

Build Tests openupm

A single-file package which provides simple Delaunay triangulation of the given set of points (float2) with mesh refinement. Implemented triangulation is based on Bowyer–Watson algorithm1 2 and refinement on Ruppert's algorithm3.

The package provides also constrained triangulation (with mesh refinement) which is based on Sloan's algorithm4.

Table of contents

Getting started

Install the package using one of the following methods

Using scoped registry (recommended) Use OpenUPM CLI or add corresponding entries to the project's manifest.json manually. Add or modify scoped registries in the manifest 
  "scopedRegistries": [
    {
      "name": "OpenUPM",
      "url": "https://package.openupm.com/",
      "scopes": [
        "com.andywiecko"
      ]
    }
  ]
and in the dependencies provide selected version of the package 
"dependencies": {
    "com.andywiecko.burst.triangulator": "2.0.0",
    ...
See Unity docs for more details https://docs.unity3d.com/2021.1/Documentation/Manual/upm-scoped.html
git install Use package manager via git install: https://github.com/andywiecko/BurstTriangulator.git.
Manual instalation Clone or download this repository and then select package.json using Package Manager (Window/Package Manager).
Copy Runtime/Triangulator.cs Since the package is single-file only, one can put the file Runtime/Triangulator.cs somewhere in the project to use it independently.

Example usage

Below one can find example usage of the Triangulator with input set as four points that form the unit square:

using var positions = new NativeArray<float2>(new float2[]
{
  new(0, 0),
  new(1, 0),
  new(1, 1),
  new(0, 1)
}, Allocator.Persistent);

using var triangulator = new Triangulator(capacity: 1024, Allocator.Persistent)
{
  Input = { Positions = positions }
};

triangulator.Run();

var outputTriangles = triangulator.Output.Triangles;
var outputPositions = triangulator.Output.Positions;

The result of the triangulation procedure will depend on selected settings. There are a few settings of the triangulation, shortly described below:

using var triangulator = new(1024, Allocator.Persistent)
{
  Settings = 
  {
    // Batch count used in parallel job.
    BatchCount = 64;
    // Triangle is considered as bad if any of its angles is smaller than MinimumAngle. Note: radians.
    MinimumAngle = math.radians(33);
    // Triangle is not considered as bad if its area is smaller than MinimumArea.
    MinimumArea = 0.015f
    // Triangle is considered as bad if its area is greater than MaximumArea.
    MaximumArea = 0.5f;
    // If true refines mesh using Ruppert's algorithm.
    RefineMesh = true;
    // If true constrains edges defined in the Triangulator.Input.ConstraintEdges
    ConstrainEdges = false;
    // If true and provided Triangulator.Input is not valid, it will throw an exception.
    ValidateInput = true;
    // Type of preprocessing algorithm, see the section below for more details.
    Preprocessor = Triangulator.Preprocessor.None;
  }
};

If the triangulation algorithm fails, checking the status and handling it in the job pipeline can be considered. For example:

[BurstCompile]
private struct Job : IJob
{
  NativeReference<Triangulator.Status>.ReadOnly status;

  public Job(Triangulator triangulator)
  {
    status = triangulator.Output.Status.AsReadOnly();
  }

  public void Execute()
  {
    if(status != Triangulator.Status.OK)
    {
      return;
    }

    ...
  }
}

...

var dependencies = default(JobHandle);
dependencies = triangulator.Schedule(dependencies);
dependencies = new Job(triangulator).Schedule(dependencies);

...

Below one can find the result of the triangulation for different selected options.

Note

To obtain the boundary from a texture, the UnityEngine.PolygonCollider was used. Generating the image boundary is certainly a separate task and is not considered in the project.

Delaunay triangulation

To use classic Delaunay triangulation make sure that constraint and refinement are disabled.

settings.RefineMesh = false;
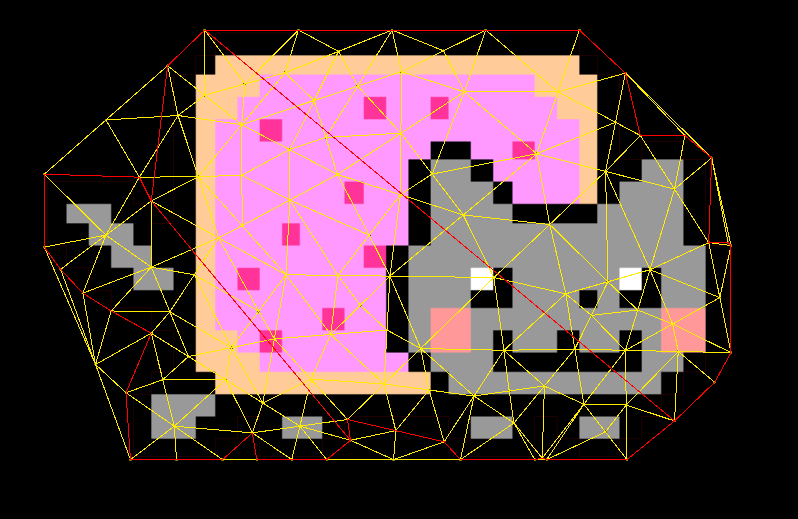
settings.ConstrainEdges = false;

The result without mesh refinement (Delaunay triangulation):

nyan-cat-without-refinement

Delaunay triangulation with mesh refinement

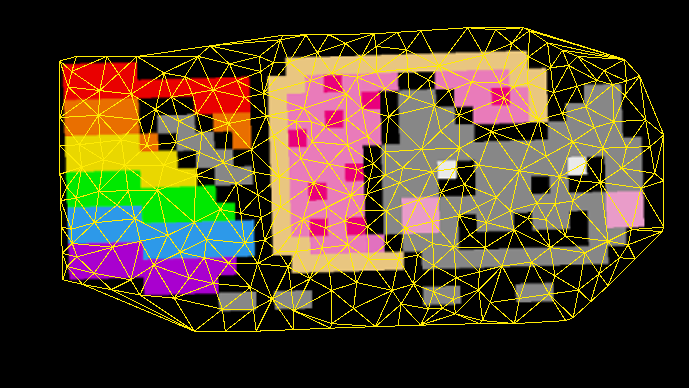
To proceed with triangulation with the mesh refinement one has to set a proper refinement option

settings.RefineMesh = true;
settings.ConstrainEdges = false;

Users can control the quality of the triangles by these options

// Triangle is considered as bad if any of its angles is smaller than MinimumAngle. Note: radians.
settings.MinimumAngle = math.radians(33);
// Triangle is not considered as bad if its area is smaller than MinimumArea.
settings.MinimumArea = 0.015f
// Triangle is considered as bad if its area is greater than MaximumArea.
settings.MaximumArea = 0.5f;

The result with mesh refinement:

nyan-cat-with-refinement

Constrained Delaunay triangulation

It is not guaranteed that the boundary of the input will be present in the classic Delaunay triangulation result. One needs to specify the constraints to resolve this issue. To specify the edges which should be present in the final triangulation provide the additional input data

triangulator.Settings.RefineMesh = false;
triangulator.Settings.ConstrainEdges = true;

// Provided input of constraint edges
// (a0, a1), (b0, b1), (c0, c1), ...
// should be in the following form
// constraintEdges elements:
// [0]: a0, [1]: a1, [2]: b0, [3]: b1, ...
using var constraintEdges = new NativeArray<int>(64, Allocator.Persistent);

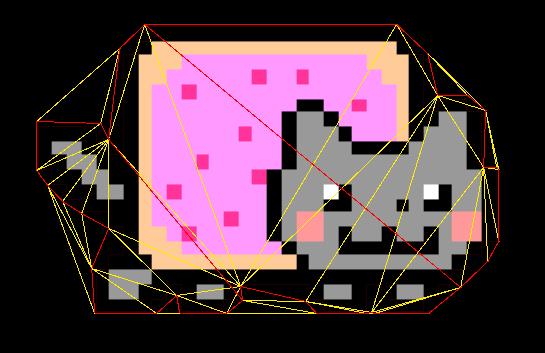
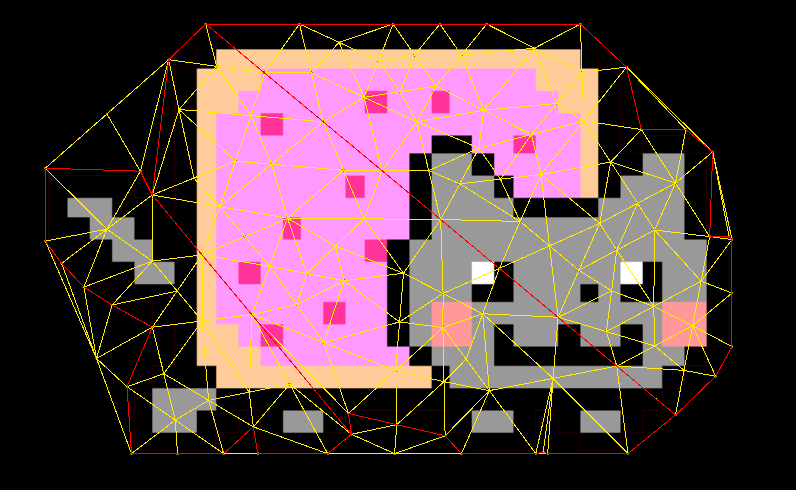
triangulator.Input.ConstraintEdges = constraintEdges;

In the following figure one can see the non-constrained triangulation result (with yellow), and user-specified constraints (with red).

nyan-cat-constraint-disabled

After enabling Settings.ConstrainEdges = true and providing the corresponding input, the result of the constrained triangulation fully covers all specified edges by the user

nyan-cat-constraint-enabled

Constrained Delaunay triangulation with mesh refinement

Constrained triangulation can be also refined in the same manner as non-constrained one, by enabling corresponding options in triangulation settings:

triangulator.Settings.RefineMesh = true;
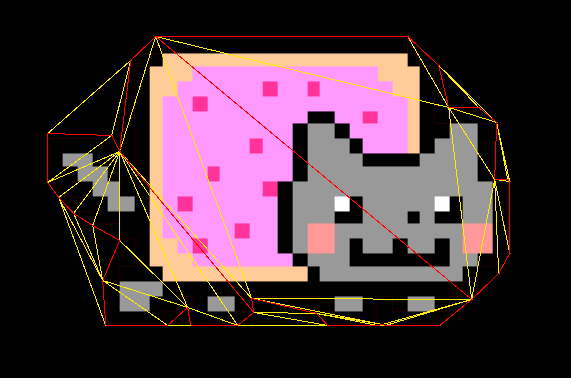
triangulator.Settings.ConstrainEdges = true;

In the following figure one can see the non-constrained triangulation result (with yellow), and user-specified constraints (with red) with the refinement.

nyan-constraint-refinement-disabled

After enabling the refinement and the constraint and providing the input, the result of the constrained triangulation fully covers all specified edges by the user and the mesh is refined with the given refinement conditions.

nyan-constraint-refinement-enabled

Support for holes and boundaries

The package provides also an option for restoring the boundaries. One has to enable corresponding options and provide the constraints

settings.RestoreBoundary = true;
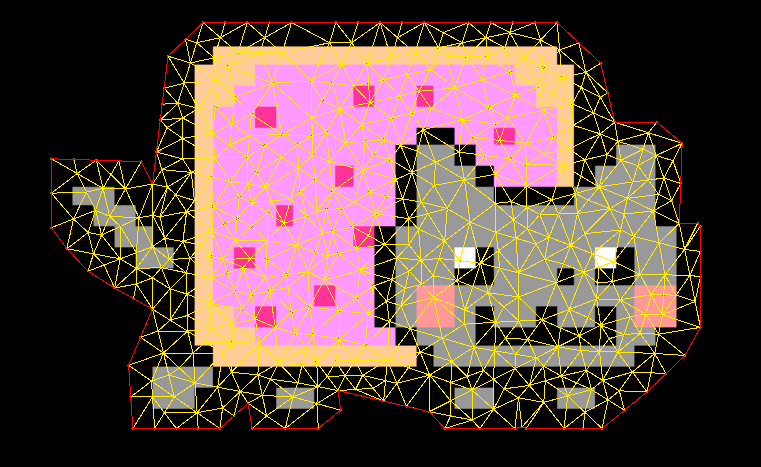
settings.ConstraintEdges = true;

In the following figure, one can see the constrained triangulation result (with yellow), and user-specified constraints (with red) with the disabled RestoreBoundary and refinement enabled.

nyan-reconstruction-disabled

After enabling the RestoreBoundary the result of the constrained triangulation fully covers all conditions and all invalid triangles are destroyed.

nyan-reconstruction-enabled

The package provides also an option for creating holes. Except for setting the ConstraintEdges, a user needs to provide positions of the holes in the same space as the Input.Positions. Enabling RestoringBoundary option is not mandatory, holes could be introduced independently of preserving the boundaries

settings.RestoreBoundary = true; // optional
settings.ConstraintEdges = true;

using var holes = new NativeArray<float2>(new[]{ math.float2(0.5f, 0.5f) }, Allocator.Persistent);
input.HoleSeeds = holes;

Summary

Below one can find the comparison of the results of all possible settings which are available in the package.

summary

Input validation

If Triangulator.Settings.ValidateInput is set to true, the provided data will be validated before running the triangulation procedure. Input positions, as well as input constraints, have a few restrictions:

  • Points count must be greater/equal 3.
  • Points positions cannot be duplicated.
  • Points cannot contain NaNs or infinities.
  • Constraint edges cannot intersect with each other.
  • Constraint edges cannot be duplicated or swapped duplicated.
  • Zero-length constraint edges are forbidden.
  • Constraint edges cannot intersect with points other than the points for which they are defined.

If one of the conditions fails, then triangulation will not be calculated. One could catch this as an error by using triangulator.Output.Status (native, can be used in jobs).

Generating input in a job

BurstTriangulation input can be generated with job pipeline. One has to use DeferredJobArrays, see the example snippet:

using var positions = new NativeList<float2>(64, Allocator.Persistent);
using var constraints = new NativeList<int>(64, Allocator.Persistent);
using var holes = new NativeList<float2>(64, Allocator.Persistent);
using var triangulator = new Triangulator(64, Allocator.Persistent)
{
  Input = 
  {
    Positions = positions.AsDeferredJobArray(),
    ConstraintEdges = constraints.AsDeferredJobArray(),
    HoleSeeds = holes.AsDeferredJobArray()
  }
}

var dependencies = new JobHandle();
dependencies = new GenerateInputJob(positions, constraints, holes).Schedule(dependencies); // Lists are fed here.
dependencies = triangulator.Schedule(dependencies);
dependencies.Complete();

Reduce the effect of roundoff error

Triangulation for non-uniform data can be demanding, and a few algorithm steps may get stuck if the data is not preprocessed properly. It is highly recommended that the user should prepare the input data on his own, however, this project provides a few built-in methods.

Preprocessor Description
None Default, no effect.
COM Transforms input into normalized local space, i.e. [-1, 1] box.
PCA Transforms input into normalized coordinate systems obtained with principal component analysis.

To use one of the following preprocessors use corresponding settings

triangulator.Settings.Preprocessor = Triangulator.Preprocessor.COM;

PCA transformation

The algorithm usually can help in situations when the Sloan algorithm gets stuck. The transformation can be applied using the following steps:

  1. Calculate com: $\mu = \displaystyle\frac1n\sum_{i=1}^n x_i$.
  2. Transform points: $x_i \to x_i -\mu$.
  3. Calculate covariance matrix: $\text{cov} = \frac1n\sum_i x_i x_i^{\mathsf T}$.
  4. Solve eigenproblem for $\text{cov}$: $\text{cov}u_i =v_i u_i$.
  5. Transform points using matrix $U = [u_i]$: $x_i \to U^{\mathsf T} .x_i$.
  6. Calculate vector center $c = \frac12[\max(x_i) + \min(x_i)]$ and vector scale $s=2/[\max(x_i) - \min(x_i)]$, where $\min$, $\max$, and "$/$" are component wise operators.
  7. Transform points: $x_i \to s (x_i-c)$, assuming component wise multiplication.

To summarize the transformation is given by:

$$ \boxed{x_i \to s[U^{\mathsf T}(x_i - \mu) - c]} $$

and inverse transformation

$$ \boxed{x_i \to U(x_i / s + c) + \mu}. $$

Note

The PCA transformation does not preserve the Settings.MinimumAngle used for refinement. As a result, triangles can be classified as bad in the PCA local space.

Benchmark

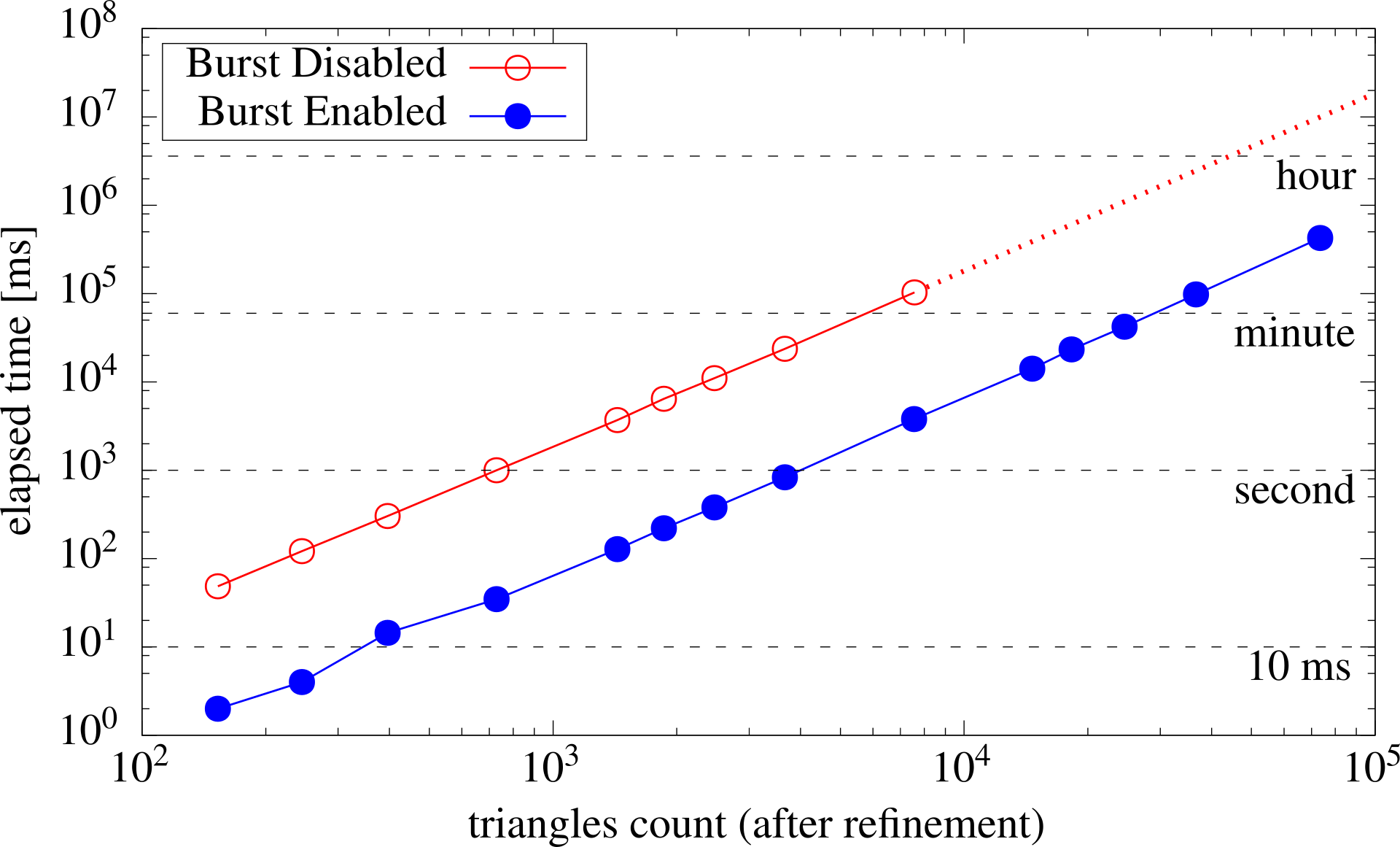
The package uses Burst compiler, which produces highly optimized native code using LLVM. Below one can see a log-log plot of elapsed time as a function of the final triangles count after mesh refinement. Using Burst can provide more or less two order of magnitude faster computation.

Note
The following figure was obtained with v1.0.

Burst Triangulator benchmark

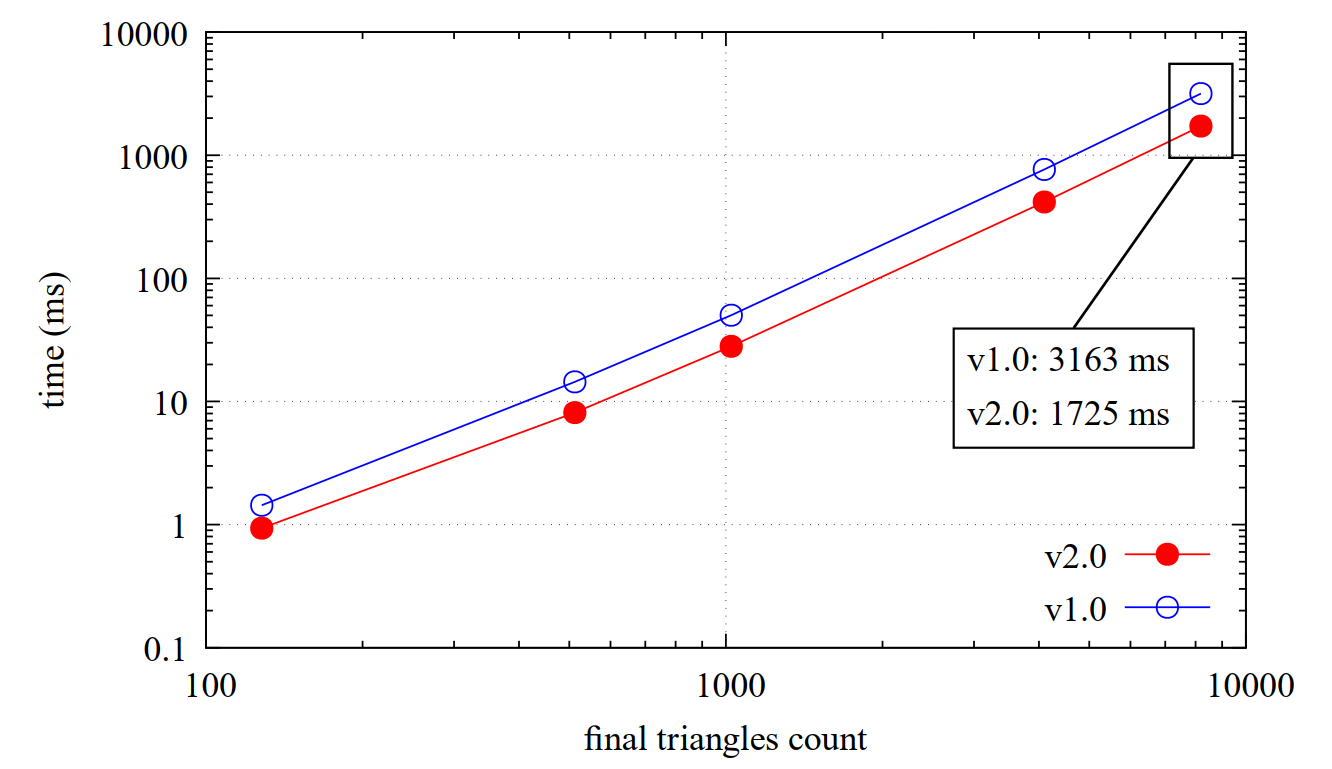
Below, you'll find a performance comparison (Burst enabled) between v1.0.0 and v2.0.0 (for the refinement task).

benchmark-v1-v2

Dependencies

Things to consider

  • Consider using BVT (or another data structure) to accelerate computing.
  • Consider caching circles for constraint edges.
  • Consider refactoring the data structure to update the edgeToTriangles buffer instead of rebuilding it.

Bibliography

Footnotes

  1. A. Bowyer. "Computing Dirichlet tessellations". Comput. J. 24 (2): 162–166 (1981). ↩

  2. D.F. Watson. "Computing the n-dimensional Delaunay tessellation with application to Voronoi polytopes". Comput. J. 24 (2): 167–172 (1981). ↩

  3. J. Ruppert. "A Delaunay Refinement Algorithm for Quality 2-Dimensional Mesh Generation". J. Algorithms 18(3):548-585 (1995). ↩

  4. S.W. Sloan. "A fast algorithm for generating constrained Delaunay triangulations." Comput. Struct. 47.3:441-450 (1993). ↩